【数据结构】红黑树(RBTree)详解——C++实现
前言
红黑树和BST树、AVL树一样,都是带有排序性质的树。那么与这两种树不同的地方在哪?为什么在C++STL中的set和map都使用的红黑树?
本文将用易于理解的描述,使得每个人都能看懂红黑树中的调整操作。
文章目录
- 前言
- 一、红黑树的定义
- 二、红黑树节点的定义
- 三、红黑树的插入理论讲解
-
- 情况1
- 情况2
- 情况3
- 结论
- 四、前置函数
- 五、旋转操作详解
-
- 左旋转操作
- 右旋转操作
- 六、插入操作代码实现
-
- 插入调整操作代码实现
- 七、红黑树删除理论讲解
-
- 情况1
- 情况2
- 情况3
- 情况4
- 结论
- 八、删除操作代码实现
-
- 删除调整操作代码实现
- RB树完整代码
一、红黑树的定义
- 每一个节点都是有颜色的,不是黑色就是红色。
- 根节点root必须是黑色的。
- 所有叶子节点都是黑色的,叶子节点是NULL节点,不存储实际的数据。
- 每个红色节点必须有两个黑色的子节点,或者说是从每个叶子节点到根节点的所有路径上不能有连续的红色节点。
- 从任一节点到其每个叶子上的所有简单路径都包含相同数目的黑色节点。
二、红黑树节点的定义
因为每个节点不是红色就是黑色,所以需要定义一个颜色相关的枚举量。
还需要操作其父节点,所以定义一个parent指针。
template<typename _Ty>
class RBTree
{
private:
// 节点颜色
enum Color
{
BLACK,
RED
};
// 节点定义
struct Node
{
Node(_Ty data = _Ty(), Node* left = nullptr,
Node* right = nullptr, Node* parent = nullptr,
Color color = BLACK)
: val_(data)
, left_(left)
, right_(right)
, parent_(parent)
, color_(color)
{}
_Ty val_;
Node* left_;
Node* right_;
Node* parent_; // 指向当前节点的父节点
Color color_; // 当前节点的颜色
};
Node* root_;
};
三、红黑树的插入理论讲解
- 如果是一个空树:则插入节点是黑色。
- 如果树非空,插入的新节点:红色!
此时要检查父节点颜色,如果父节点是黑色,插入完成;
如果父节点是红色,则出现连续的红色节点,就要开始做红黑树的插入调整操作:
情况1
父节点是红色,爷爷节点是黑色,且三者在同一侧。
如图新插入的节点C,如果父节点是红色,则为了保持红黑树的第4条性质,需要交换父亲节点和爷爷节点的颜色:
从局部图来看,这样似乎没错,但考虑不周,在这里还需要考虑爷爷节点的另一个孩子节点,这里叫作叔叔节点,如果叔叔节点本身为红色,那么经过这样交换后,又不满足红黑树性质了。所以正确的情况为:
即使到了这一步,也不要觉得完成了,我们把新节点的爷爷节点的颜色改成红色了,这时候还需要考虑两种情况
- 如果爷爷节点的父节点也是红色,那又不满足红黑树性质,将x指向爷爷节点,继续调整。
- 爷爷节点是根节点,则强制将根节点置为黑色。
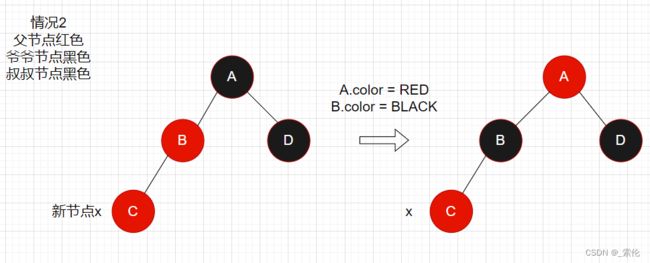
情况2
插入节点的父节点是红色,爷爷节点是黑色,三者在同一侧,叔叔节点是黑色。
为了满足红黑树性质,需要将其父节点颜色与爷爷节点颜色进行交换。
出现的问题:将爷爷节点A改成红色,那么就会导致从根节点到节点D的这条路径中,少一个黑色节点。不满足红黑树第5条性质(所有路径的黑色节点数量相等)。
解决方案:以A节点为参数做右旋转操作,旋转完成后,符合红黑树的性质,调整完成。
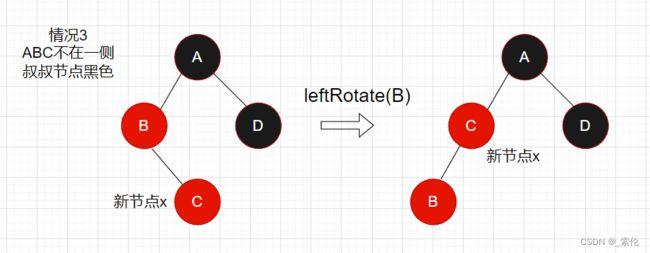
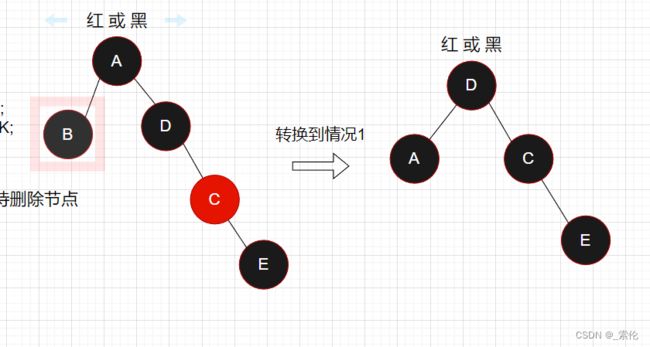
情况3
父节点是红色,爷爷节点是黑色,三者不在一侧,叔叔节点是黑色。
如图:如果直接调整颜色,那么还是会影响红黑树的第5个性质,所以可以先将三者旋转成同一侧,显然,这里需要对父节点B做左旋转,旋转后如图
将其旋转完成后,ABC处于同一侧,这时候再说如何改变颜色,但通过观察,旋转完成后,变成和情况2是一个情况,所以直接让其转到情况2的操作:
结论
上面的三种情况,都是插入的节点在爷爷节点的左孩子上,那么与之对应的,右边也有相应的三种情况,所以红黑树的插入调整,一共有六种调整。
总结:红黑树的插入最重要的是考虑叔叔节点的颜色。
四、前置函数
// 返回节点颜色
Color getColor(Node* node)
{
return node == nullptr ? BLACK : node->color_;
}
// 设置颜色
void setColor(Node* node, Color color)
{
node->color_ = color;
}
// 返回节点的左孩子
Node* getLeft(Node* node)
{
return node->left_;
}
// 返回节点的右孩子
Node* getRight(Node* node)
{
return node->right_;
}
// 返回节点的父节点
Node* getParent(Node* node)
{
return node->parent_;
}
五、旋转操作详解
左旋转操作
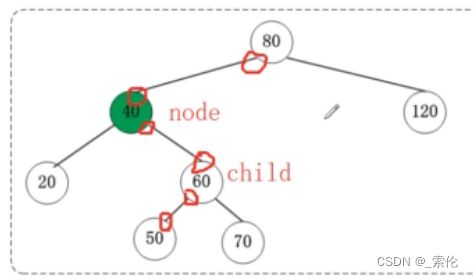
如图,对node进行左旋转操作,它和AVL树的左旋转有什么区别?
AVL树左旋转代码:
// 左旋转操作
void leftRotate(Node* node)
{
Node* child = node->right_;
node->right_ = child->left_;
child->left_ = node;
}
由于红黑树多出了parent指针,所以在旋转时,要更改六个地址:
加上对parent操作的代码:
- 让child的parent指向node本身的parent,如果node的parent为NULL,则说明node就是根节点,则直接将根节点指向child;
- 如果node的parent不为NULL,则让node的parent的左孩子或右孩子指针指向child;
- 接下来更改child的左孩子,如果存在左孩子,就将左孩子的parent指针指向node;
- 最后更改node的parent指针,将其指向child。
// 左旋转操作
void leftRotate(Node* node)
{
Node* child = node->right_;
child->parent_ = node->parent_;
if (node->parent_ == nullptr)
{
root_ = child;
}
else
{
if (node->parent_->left_ == node)
{
// node在父节点的左孩子
node->parent_->left_ = child;
}
else
{
// node在父节点的右孩子
node->parent_->right_ = child;
}
}
node->right_ = child->left_;
if (child->left_ != nullptr)
{
child->left_->parent_ = node;
}
child->left_ = node;
node->parent_ = child;
}
右旋转操作
代码实现和左旋转刚好相反
// 右旋转
void rightRotate(Node* node)
{
Node* child = node->left_;
child->parent_ = node->parent_;
if (node->parent_ == nullptr)
{
// node原来就是root节点
root_ = child;
}
else
{
if (node->parent_->left_ == node)
{
node->parent_->left_ = child;
}
else
{
node->parent_->right_ = child;
}
}
node->left_ = child->right_;
if (child->right_ != nullptr)
{
child->right_->parent_ = node;
}
child->right_ = node;
node->parent_ = child;
}
六、插入操作代码实现
基于BST树的插入代码
// 插入操作
void insert(const _Ty& data)
{
if (root_ == nullptr) // 1
{
root_ = new Node(data);
return;
}
Node* parent = nullptr; // 2
Node* cur = root_; // 3
while (cur != nullptr)
{
if (cur->val_ > data) // 4
{
parent = cur;
cur = cur->left_;
}
else if (cur->val_ < data) // 5
{
parent = cur;
cur = cur->right_;
}
else
{
return; // 遇到重复的,则什么都不做 // 6
}
}
// 设置当前节点的parent和颜色
Node* node = new Node(data, nullptr, nullptr, parent, RED); // 7
if (parent->val_ > data)
{
parent->left_ = node;
}
else
{
parent->right_ = node;
}
// 如果新插入的红色节点,父节点也是红色,
// 则不满足红黑树性质,进行插入调整操作
if (RED == getColor(parent)) // 8
{
fixAfterInsert(node);
}
}
- 如果根节点为nullptr,则以data为根节点的值,构建根节点;
- parent指针,跟踪当前节点;
- cur指针,初始化指向根节点,查找的作用,用来找待插入位置;
- 如果cur的值大于待插入元素,则让parent指针指向当前节点,当前节点向左子树走;
- 如果cur的值小于待插入元素,则让parent指针指向当前节点,当前节点向右子树走;
- 上面两个情况不满足,说明遇到重复值了,直接退出;
- 申请新节点,设置新节点的指针域和颜色,新节点都为红色。再根据与当前parent节点的值域大小关系,将其挂到左子树或右子树上面;
- 插入完成后,就会面临上面提到的六种情况,涉及到更改颜色和旋转操作,这里写一个函数专门实现。
插入调整操作代码实现
该函数的作用就是在进行插入完成后,为了保证红黑树性质,所做出的调整(修正)操作,涉及更改颜色,旋转操作。
// 红黑树的插入调整操作
void fixAfterInsert(Node* node)
{
// 如果当前红色节点的父节点也是红色
while (RED == getColor(getParent(node))) // 1
{
// 如果当前节点的父节点是爷爷节点的左孩子
if (getLeft(getParent(getParent(node))) == getParent(node)) // 2
{
// 插入的节点在左子树
// 找到叔叔节点,改变颜色
Node* uncle = getRight(getParent(getParent(node))); // 3
if (RED == getColor(uncle)) // 情况1:叔叔节点是红色
{
setColor(uncle, BLACK);
setColor(getParent(node), BLACK);
setColor(getParent(getParent(node)), RED);
// 继续调整上面的
node = getParent(getParent(node)); // 4
}
else
{
// 先处理情况三,转成情况二
if (getRight(getParent(node)) == node) // 5
{
node = getParent(node);
leftRotate(node);
}
// 6 处理情况二
setColor(getParent(node), BLACK);
setColor(getParent(getParent(node)), RED);
rightRotate(getParent(getParent(node)));
break; // 调整完成
}
}
else // 7
{
// 插入的节点在右子树
Node* uncle = getLeft(getParent(getParent(node)));
if (RED == getColor(uncle)) // 情况1:叔叔节点是红色
{
setColor(uncle, BLACK);
setColor(getParent(node), BLACK);
setColor(getParent(getParent(node)), RED);
// 继续调整上面的
node = getParent(getParent(node));
}
else
{
// 先处理情况三,转成情况二
if (getLeft(getParent(node)) == node)
{
node = getParent(node);
rightRotate(node);
}
// 处理情况二
setColor(getParent(node), BLACK);
setColor(getParent(getParent(node)), RED);
leftRotate(getParent(getParent(node)));
break; // 调整完成
}
}
}
// 强制root_为黑色
setColor(root_, BLACK); // 8
}
这里可以配合上面的图片来理解:
- 使用一个while循环,用来判断当前节点的父节点是否是红色,因为在更改完成后,染成红色的节点的父节点有可能还是红色;
- 如果当前节点的父节点是爷爷节点的左孩子,则就是上面讲解的三种情况之一,处理这三种情况即可;
- 先利用一个uncle指针记录叔叔节点,如果叔叔节点是红色,则说明是情况1,处理操作:(1)将父节点置为BLACK,(2)将叔叔节点置为BLACK,(3)将爷爷节点置为RED。
- 将node指针指向爷爷节点,继续循环 向上调整;
- 如果叔叔节点是黑色,则属于第2,3种情况。这里先处理第3种,因为第3种情况可以转化为第2种。处理操作:判断当前节点是否是父节点的右孩子,如果是,则让node指向父节点,对父节点进行左旋转操作;
- 然后集中处理第2种情况:(1)将父节点置为BLACK,(2)将爷爷节点置为RED,(3)对当前点的爷爷节点进行右旋转操作,(4)跳出循环,执行第8步操作;
- else为其他三种情况,即插入节点在爷爷节点的右边,这里的操作与上面刚好相反,只需要更改与方向相关的操作即可;
- 为保证红黑树性质,结束时强制将根节点置为BLACK。
七、红黑树删除理论讲解
红黑树的删除,按找孩子节点划分,可分为:
- 删除有两个孩子的节点,这种可转换为删除前驱节点;
- 删除有一个孩子的节点,将孩子节点挂到父节点上;
- 没有孩子节点。
这一部分的代码可以直接参考BST树。
按照删除节点的颜色划分,可分为:
- 删除一个红色节点,就是一个BST树的删除,不用做调整操作;
- 删除一个黑色节点,那么就会有两种情况:
(1)如果补上来的孩子是红色节点,直接把这个孩子涂成黑色,调整完成。
(2)如果补上来的孩子是黑色节点,那么在当前这个路径上没办法再补一个黑色节点出来,只能从兄弟节点借调一个黑色节点。
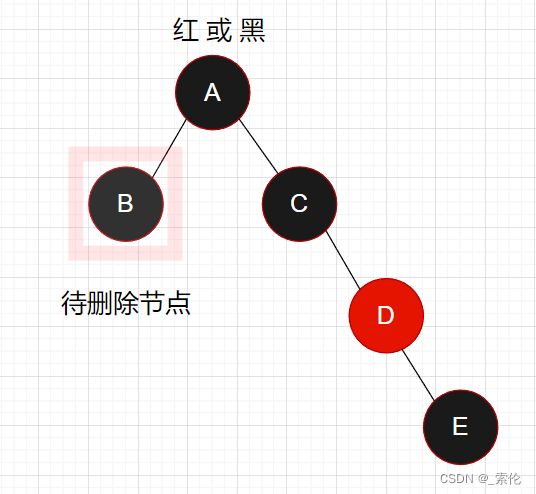
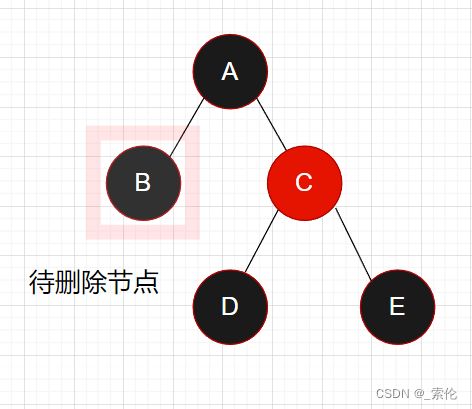
情况1
删除的节点在父节点左边,右边的兄弟是黑色,兄弟节点的右孩子节点是红色。
如图,删除的B节点是黑色节点,为了保证红黑树的性质,需要从兄弟节点C借一个黑色节点,这时候需要C节点的孩子是红色,因为可以将其染成黑色,来保证红黑树的性质。
解决方案:
(1)交换父节点A和兄弟节点C的颜色;
(2)把兄弟节点的孩子节点置为黑色;
(3)对父节点A做一个左旋转操作。
情况2
删除的节点在父节点左边,右边的兄弟节点是黑色,兄弟节点的左孩子是红色。
如下图,这种情况下不能像情况1那样,直接从兄弟节点借调一个,因为兄弟节点C右边的路径上没有红色节点用以涂成黑色。
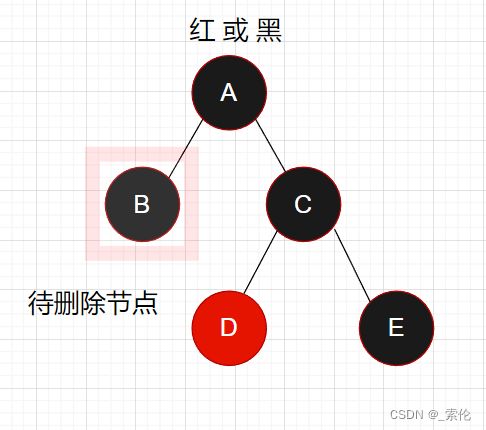
解决方案:
(1)对兄弟节点进行右旋转,使得C的左孩子和C在一条路径上,得到下图中的图2;
(2)为了保证红黑树性质,需要将D和C节点的颜色交换(A可能为红色,不能出现连续红色);
(3)接下来是不是很熟悉,就是转换成了上面的情况1;
情况3
删除节点是父节点左孩子,兄弟节点是黑色,兄弟节点的两个孩子节点都是黑色。
这种情况下,不能从兄弟节点那里借调。可以选择的方法是:直接将兄弟节点染成红色。
将兄弟节点涂成红色后,还要检查父节点颜色,如果是红色,则出现连续红色,需要调整,将其父节点染成黑色;
如果是黑色,则向上回溯,查看是否是其他情况。
情况4
待删除节点是左孩子,兄弟节点是红色。
调整目的还是和上面一样,先给待删除节点找一个黑色兄弟节点。
解决方案:
(1)将兄弟节点C和父节点A的颜色进行交换;
(2)对父节点A做左旋转操作,这样就会给待删除节点B匹配一个黑色的兄弟节点;
(3)然后转换为上面三种情况。
结论
有上面的四种情况,那就有其镜像的情况,所以删除调整操作一共有8种情况。
总结:删除最重要的是看兄弟节点颜色。
八、删除操作代码实现
同样是基于BST树的删除:
// 删除操作
void remove(const _Ty& data)
{
if (root_ == nullptr) // 1
{
return;
}
Node* cur = root_; // 2
while (cur != nullptr)
{
if (cur->val_ > data)
{
cur = cur->left_;
}
else if (cur->val_ < data)
{
cur = cur->right_;
}
else
{
break;
}
}
// 没找到节点,返回 // 3
if (cur == nullptr)
{
return;
}
// 删除前驱节点 情况三 // 4
if (getLeft(cur) != nullptr && getRight(cur) != nullptr)
{
Node* pre = cur->left_; // 5
while (getParent(pre) != nullptr)
{
pre = pre->right_;
}
cur->val_ = pre->val_;
cur = pre; // cur指向前驱节点
}
// 删除cur指向的节点 情况一和二 // 6
Node* child = cur->left_; // 让child指向不为空的孩子
if (child == nullptr)
{
child = cur->right_;
}
// left right parent
if (child != nullptr) // 7
{
child->parent_ = cur->parent_;
if (getParent(cur) == nullptr)
{
root_ = child; // 8
}
else // 9
{
if (getLeft(getParent(cur)) == cur)
{
cur->parent_->left_ = child;
}
else
{
cur->parent_->right_ = child;
}
}
Color c = getColor(cur); // 10
delete cur;
// 如果删除的黑色节点,需要调整到满足红黑树性质 // 11
if (c == BLACK)
{
fixAfterRemove(child);
}
}
else // child == nullptr
{
if (getParent(cur) == nullptr) // 12
{
delete cur;
root_ = nullptr;
return;
}
else
{
// 删除的cur是叶子节点
if (BLACK == getColor(cur)) //13
{
fixAfterRemove(cur);
}
if (getLeft(getParent(cur)) == cur) // 14
{
cur->parent_->left_ = nullptr;
}
else
{
cur->parent_->right_ = nullptr;
}
delete cur;
}
}
}
- 如果根节点为nullptr,则不做任何操作;
- 定义一个指向当前节点的指针,在树中查找待删除节点;
- 跳出循环后如果cur指向nullptr,则直接返回;
- 删除节点有三种情况,(1)待删除节点没有孩子(2)待删除节点有一个孩子(3)待删除节点有两个孩子;
- 先处理情况3,如果有两个孩子,则将问题转换为删除其前驱节点,找到后,cur指向前驱节点。
- 然后处理情况1和2,定义child指针指向cur非空孩子;
- 如果child不为nullptr,接下来该处理节点的parent指针域了,这里先让child的parent指针指向cur的parent;
- 如果cur的parent为nullptr,说明cur是根节点,则将child置为根节点;
- 如果不是根节点,则将child挂到cur的parent节点的左孩子或右孩子(cur以前在哪个孩子,就把child挂到相应位置);
- 保存待删除节点cur的颜色后,将其删除掉;
- 如果删除的是黑色节点,则为了满足红黑树性质,需要删除后调整,即上面讲解到的8种情况;
- 接下来的情况与第七点开始相反,如果child为nullptr,说明删除的cur可能是叶子节点或根节点。如果此时cur的parent为nullptr说明删除的根节点,则将根节点删除后置为nullptr,然后返回;
- 如果删除的cur是叶子节点,则再次判断其颜色,如果为黑色,则需要删除调整操作;
- 调整后,再判断删除的是父节点的左孩子还是右孩子,将其对应位置置为nullptr,然后delete掉cur。
删除调整操作代码实现
调整操作一共八种情况,左右各四种,理论讲解完后,现在实现代码:
// 红黑树的删除调整操作
void fixAfterRemove(Node* node)
{
while (getColor(node) == BLACK) // 1
{
if (getLeft(getParent(node)) == node) // 2
{
// 删除的黑色节点在左子树
Node* brother = getRight(getParent(node)); // 3
if (getColor(brother) == RED) // 情况四 // 4
{
// 交换父节点和兄弟节点颜色
setColor(getParent(node), RED);
setColor(brother, BLACK);
leftRotate(getParent(node));
brother = getRight(parent(node));
}
// 兄弟是黑色 // 5
if (getColor(getLeft(brother)) == BLACK
&& getColor(getRight(brother)) == BLACK) // 情况三 // 6
{
setColor(brother, RED);
node = getParent(node);
}
else
{
if (getColor(getRight(brother)) != RED) // 情况二 // 7
{
setColor(brother, RED);
setColor(getLeft(brother), BLACK);
rightRotate(brother);
brother = getRight(getParent(node));
}
// 归结为情况一 // 8
setColor(brother, getColor(getParent(node)));
setColor(getParent(node), BLACK);
setColor(getRight(brother), BLACK);
leftRotate(getParent(node));
break;
}
}
else // 9
{
// 删除的黑色节点在右子树
Node* brother = getLeft(getParent(node));
if (getColor(brother) == RED)
{
// 交换父节点和兄弟节点颜色
setColor(getParent(node), RED);
setColor(brother, BLACK);
rightRotate(getParent(node));
brother = getLeft(getParent(node));
}
// 兄弟是黑色
if (getColor(getLeft(brother)) == BLACK
&& getColor(getRight(brother)) == BLACK) // 情况三
{
setColor(brother, RED);
node = getParent(node);
}
else
{
if (getColor(getLeft(brother)) != RED) // 情况二
{
setColor(brother, RED);
setColor(getRight(brother), BLACK);
leftRotate(brother);
brother = getLeft(getParent(node));
}
// 归结为情况一
setColor(brother, getColor(getParent(node)));
setColor(getParent(node), BLACK);
setColor(getLeft(brother), BLACK);
rightRotate(getParent(node));
break;
}
}
}
// 如果发现node指向的节点是红色,直接涂成黑色,调整结束
setColor(node, BLACK); // 10
}
- 首先,只有待删除节点为黑色时,才进入删除调整函数,所以最外层循环就是判断该节点是否为黑色;
- 判断删除节点是否在父节点的左子树,接下来处理位于左子树的四种情况;
- 定义一个brother节点指向该节点的兄弟节点,即父节点的右孩子,在上面的理论讲解完毕后,总结出来,删除调整操作的关键是兄弟节点;
- 上面说到根节点每一侧有四种情况,现在先处理第四种(兄弟节点是红色)。解决方案:(1)将兄弟节点和父节点的颜色进行交换;(2)对父节点做左旋转操作,这样就会给待删除节点匹配一个黑色的兄弟节点;(3)然后转换为前三种情况;
- 接下来处理兄弟节点是黑色的;
- 先处理情况三(兄弟节点的两个孩子都是黑色)。解决方案:将兄弟节点涂成红色后,检查父节点颜色,如果是红色,则出现连续红色,需要调整,将其父节点染成黑色;如果父节点是黑色,则向上回溯,查看是否是其他情况。
- 接下来处理情况二(兄弟节点的左孩子是红色,右孩子不是红色)。解决方案:(1)将兄弟节点和左孩子的颜色进行交换。(2)对兄弟节点进行右旋转,使得兄弟的左孩子成为兄弟节点的父节点。(3)转换为情况1;
- 接下来处理情况1(兄弟节点的右孩子是红色)。解决方案:(1)交换父节点和兄弟节点的颜色。(2)将兄弟节点的右孩子涂成黑色。(3)对根节点进行左旋转,这步操作后,原兄弟节点称为新根,而且保证了红黑树的性质;
- 从这里开始,与从步骤2到步骤8的情况相反,上面的描述是待删除节点是父节点的左孩子,接下来的步骤为:待删除的节点是父节点的右孩子,只需要修改所有与方向相关的代码即可;
- 整个循环结束后,如果发现根节点为红色,则强制将根节点置为黑色,调整完成!
RB树完整代码
#include