数据拟合、参数估计、插值等数据处理算法

介绍

1. 数据拟合：
   数据拟合是通过选择或构建合适的函数模型，将给定的数据点与该函数模型进行匹配和拟合的过程。常见的数据拟合方法包括最小二乘法和非线性最小二乘法。最小二乘法通过最小化实际数据与拟合函数的残差平方和来求解最优拟合参数。非线性最小二乘法则通过迭代优化算法来拟合非线性函数模型。

2. 参数估计：
   参数估计是利用给定的数据，通过估计参数的值来拟合一个数学模型。参数估计的目标是找到最符合数据的参数组合，使模型的预测值与实际观测值最接近。常用的参数估计方法包括最大似然估计和最小二乘估计。最大似然估计通过选择使观测数据出现的概率最大化的参数值来估计模型的参数。最小二乘估计则是通过最小化误差平方和来估计参数。

3. 插值：
   插值是根据已知数据点的值，通过定义适当的插值函数或多项式来估计在两个已知数据值之间的未知数据值。常见的插值方法包括线性插值、多项式插值和样条插值。线性插值是通过线性函数在两个已知数据点之间进行插值。多项式插值则是通过构造一个多项式函数来连接已知数据点并进行插值。样条插值则是使用分段的低次多项式来进行插值，以获得更平滑和连续的曲线。

举例

数据拟合：

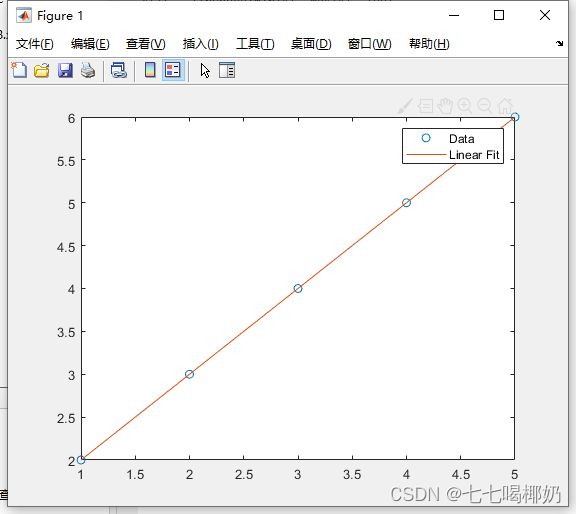
假设我们有一组散乱的数据点，并且我们希望用一条直线来拟合这些数据。在Matlab中，可以使用polyfit函数进行最小二乘线性拟合。

% 假设有一组数据点
x = [1, 2, 3, 4, 5];
y = [2, 3, 4, 5, 6];

% 进行线性拟合
p = polyfit(x, y, 1);

% 绘制原始数据和拟合线
plot(x, y, 'o');
hold on;
xfit = linspace(min(x), max(x), 100);
yfit = polyval(p, xfit);
plot(xfit, yfit);
legend('Data', 'Linear Fit');

参数估计：

假设我们有一组观测数据，并且我们希望通过最大似然估计来估计这些数据的分布参数。在Matlab中，可以使用mle函数进行最大似然估计。

% 假设我们观测到一组来自正态分布的数据
data = normrnd(5, 2, [1, 100]);

% 进行最大似然估计
params = mle(data, 'distribution', 'normal');

% 打印估计参数
mu = params(1);
sigma = params(2);
fprintf('Estimated mean: %f\n', mu);
fprintf('Estimated standard deviation: %f\n', sigma);

插值：

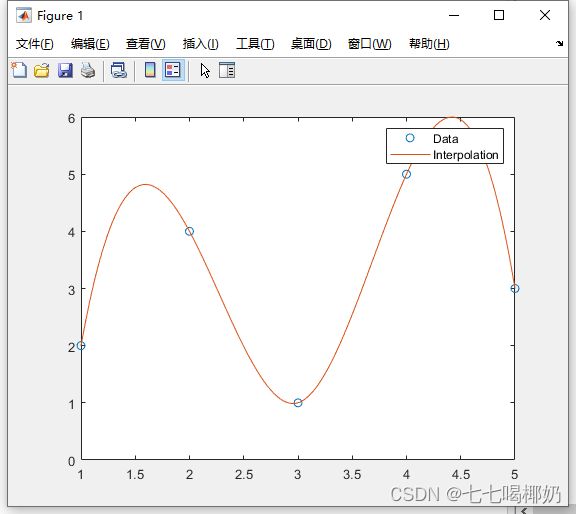
假设我们有一些离散的数据点，并且我们希望通过插值来估计这些数据点之间的未知值。在Matlab中，可以使用interp1函数进行插值。

% 假设我们有一些离散的数据点
x = [1, 2, 3, 4, 5];
y = [2, 4, 1, 5, 3];

% 进行插值
x_interp = linspace(min(x), max(x), 100);
y_interp = interp1(x, y, x_interp, 'spline');

% 绘制原始数据和插值曲线
plot(x, y, 'o');
hold on;
plot(x_interp, y_interp);
legend('Data', 'Interpolation');