数据结构与算法 | 第四章：字符串

本文参考网课为 数据结构与算法 ¹ 第四章字符串，主讲人 张铭 、王腾蛟 、赵海燕 、宋国杰 、邹磊 、黄群。

本文使用IDE为 Clion，开发环境 C++14。

更新：2023 / 11 / 12

---

---

字符串

概念

字符串

字符串 是一类简单的由 字符（ char）构成的线性结构的 线性表。

字符串 简称 串，为零个或多个 字符 / 符号 构成的有限序列。
n (>=0) 个 字符 的有限序列，一般记作 S C₀C₁…C_n-1。

• S 为串名
• C₀C₁…C_n-1为串值。C_i中i位置上的 字符 / 符号
• n 为字符串长度。长度为零的串，不包含任何字符内容。理论上，一个字符串的长度可以为任意的有限长度，实际上：
  • 定长
    具有固定的最大长度，所用内存量始终如一
  • 变长
    根据实际需要伸缩，以提高内存空间利用率

字符

字符 的取值依赖于字符集。常用的字符集包括：

• 由 {0, 1} 所构成的二进制字符集
• 由4个字符组成的生物信息的DNA字符集
• 由26个字符和标点符号等组成的英语语言
• 由6763个常用汉字和682个全角非汉字符号等所构成的简体中文标准字符集GB2312
• 适用于跨语言、跨平台的通用字符集USC（ Universal Character Set ）

这些 字符 在计算机里是如何存储和运算呢？这就需要 字符编码 来建立 字符集 与计算机数字系统之间的对应关系。

字符编码

字符编码 会将 字符集 里的每一个字符编码为由0和1组成的序列。那么，具体，哪一个二进制序列表示哪一个符号则取决于我们所使用的编码方式。常用的编码方式有：

• ASCII 编码
  • 使用单字节（ 8 bits ）对字符集 charset 的128个符号进行编码
  • 基于拉丁字母的编码，主要用于现代英语和多种西欧语言，也为大多数程序设计语言所采用，例如C和C++
• 其他编码方式
  • ANSI 编码
    支持多种东方语言：GB2312、BIG5、JIS 等。不同国家/地区制定不同的标准，不同 ANSI 编码间互不兼容
  • Unicode（跨语言跨平台）
    各种语言中的每一个字符具有唯一的数字编号，便于跨平台的文本转换

无论采用哪一种编码方式，对于一个给定字符集中的字符编码需要满足一组无歧义的规则，使得字符集中的每一个字符都对应唯一的一个编码。且不同的字符编码之间要满足偏序关系。
所谓偏序关系，是定义在集合上的一个二元关系满足自反性、反对称性和传递性。在偏序规则下，

• 连续的数字 0 - 9 是要连续编码的。像在 ASCII 编码 下，0 的编码是 48，那么 1 的编码就是 49。
• 连续的字符也是需要连续编码的。像在 ASCII 编码 下，大写字母 A 的编码是65，那么 B 的编码就是66。

通常在字符偏序下，根据字符的自然含义，两个字符之间是可以根据它的编码值进行直接的比较的。两个字符串就会按照构成的字符之间的编码进行大小的比较来得到字典序。

子串

一个 字符串 中任意个连续的字符组成的子序列称为该串的 子串 。

比如说一个长度为 n 的字符串 s₁ 和长度为 m 的 s₂，0<=m<=n。若存在整数 j (0<=i<=n-m) 使得 b_j = a_i+j，j = 0，1，…，m-1同时成立，则称串 s₂ 是串 s₁ 的字串，或称 s₁ 包含串 s₂。
另外，空串是任意串的子串。任意串S都是其自身的子串。

子串 相关的应用有：提取、插入、寻找、删除等等。

抽象数据类型

int length();                                   // 返回串的长度
int isEmpty();                                  // 判断串是否为空串
int find(const char c, const int s);            // 从s开始搜索串寻找一个给定字符
int strcmp(const char *s1, const char *s2);     // 串比较

void clear();                           		// 清空串

string substr(const int s, const int len);      // 从s开始提取一个长度为len的子串
string insert(const char s, const int index);   // 往串中给定位置插入一个字符
string append(const char c);                    // 往串尾添加字符
string concatenate(const char *s);              // 往本串后面链接串s

char *strcpy(char *s1, const char *s2);         // 串复制

存储与实现

字符串 是一种基本元素为 字符 的特殊线性表，所以本质上它的存储也有线性表的顺序和链式两种方式。但是对于 字符串 这类特殊的线性表来说，链式存储的结构性开销过大而很少被采用，所以我们主要以顺序存储为主来介绍 字符串 的存储与实现。

顺序存储

对于定长的 字符串 采用顺序存储方式，即事先申请固定长度的空间但需要有相应的机制来确切的知道当前串的长度。所以一般有3种处理方案：

• 用 字符串 的第一个元素 S[0] 作为记录串长的存储单元
  缺点：该方式决定串的最大长度不能超过256 ²。
• 另辟空间存储串的长度
  缺点：串的最大长度一般是静态给定的，而非动态申请
• 特殊标记串的结束
  C / C++ 的标准字符串（ #include ）

C / C++的标准字符串

C / C++ 的标准字符串是将字符串变量定义为字符数组 char s[M]。

字符串的结束标记是 ASII码中8位全0码 ‘\0’，亦称 NULL。因此，字符串的实际长度为 M-1。
例如，chars s1[6]='value';，定义了一个名为 chars 的字符数组，长度为6位，但是只能存储5位字母。

需要注意的是，标准串定义成了数组，所以它是无法作为左值被赋值的。例如，s1 = s2 是不合规的。

标准串运算

函数库 提供字符串处理函数来方便字符串的运算。下面是 string.h 提供的一些常用的字符串的操作：

函数	作用
int strlen(char *s)	串长
char *strcpy(char *s1, char*s2);	串复制
char *strcat(char *s1, char *s2);	串拼接
int strcmp(char *s1, char *s2);	串比较
char *strchr(char *s, char c);	字符定位
char *strrchr(char *s, char c);	字符定位
int *strstr(char* s2, char* s1)	子串抓取

字符串长度

• 1. 求字符串的长度

int strlen(char s[])
{
    int i = 0;
    while (s[i] != 0)
        i ++;
    return i;
}

• 2. 比较2个字符串的长度

int strcmp(const char *s1, const char *s2)          // 定义2个字符串，分别为s1、s2
{
    int i = 0;
    while (s2[i] != '\0' && s1[i] != '\0'){         // 字符串的结束标记为 \0
        if (s1[i] > s2[i])
            return 1;                               // s1比s2长
        else if (s1[i] < s2[i])
            return -1;                              // s1比s2短
        i ++;
    }
    if (s1[i] == '\0' && s2[i] != '\0')
        return -1;                                  // s1比s2短
    else if (s2[i] == '\0' && s1[i] != '\0')
        return 1;                                   // s2比s1短
    return 0;
}

或者，

int strcmp_1(char *s1, char *s2)                // 定义2个字符串，分别为s1、s2
{
    int i;
    for (i=0; s1[i] == s2[i]; ++i){
        if (s1[i] == '\0' && s2[i] == '\0')
            return 0;                           // 两个字符串相等
    }
    return (s1[i]-s2[i])/abs(s1[i]-s2[i]);      // 不等，比较第一个不同的字符
}

字符串寻找字符

• 1. 在字符串 s 中正向寻找字符 c

char * strchr(char *s, char c)
{
    i = 0;
    while (s[i] != '\0' && s[i] != c)       // 循环跳过非c字符
        i++;
    // 在循环结束后
    if (s[i] == '\0')                       // 当s不包含字符c则在s[i]即串尾
        return 0;
    else                                    // 当s[i]==c则返回s[i]
        return &s[i];
}

• 2. 在字符串 s 中反向寻找字符 c

char * strrchr(char *s, char c)
{
    i = 0;
    while (s[i] != '\0') i++;               // 获得s字符串的长度
    while (s[--i] != '\0' && s[i] != c);    // 循环反向跳过非c字符
    // 在循环结束后
    if (s[i] == '\0')                       // 当s不包含字符c则在串尾结束
        return 0;
    else                                    // 若成功则返回相应位置
        return &s[i];
}

举例，在 s = [Hello world\0] 中寻找 o：

寻找字符 o，strchar(s, 'o') 返回 4；
反向寻找 o，strchar(s, 'o') 返回 7。

C++的字符串类 String

除了采用标准字符串以外，还可以采用字符串类 String 来表示和存储字符串，以适应字符串的长度动态变化。

在 String 类中，字符串不再是以字符数组 char S[M] 这种形式来直接出现，而是采用一种动态变长的存储结构。

String 类是通过实例化标准模板库中的 STL 的 basic_string 而得到的。如下：

typedef basic_string <char> string;

它的存储结构如下：

private:                // 具体实现的字符串存储结构
    char *str;                          // 字符指针表示的串实体
    int size;                           // 字符串长度
public:                 // 成员函数
    String(char *s);                    // 构构子
    ~String();                          // 析构子
    String operator=(String & s);       // 赋值
    String operator+(String);           // 拼接
    String substr(int index, int cout); // 子串
    int find(char c, int start);        // 查找
    ...

字符串类运算

操作类别	方法	描述
子串	substr	返回一个串的子串
拷贝 / 交换	copy	将一个串拷贝到另一个串中
	swap	交换两个串的内容
赋值	assign	把一个串、一个字符、一个子串赋值给另一个串中
	=	把一个串或一个字符赋值给另一个串中
插入 / 追加	insert	在给定位置插入一个字符、多个字符或串
	+=	将一个字符或串追加到另一个串后
	append	将一个或多个字符，或串追加在另一个串后
拼接	+	通过将一个串放置在另一个串后面来构建新的新串
查询	find	找到并返回一个子序列的开始位置
替换 / 清除	replace	替换一个指定字符或一个串的子串
	clear	清除串中的所有字符
统计	size	返回串中字符的数目
	length	返回size()
	max_size	返回串允许的最大长度

构造算子

String 类有多个构造函数。构造一个带有初始值的 String 类可以参照以下方法：

String::String(char *s){        // 确定新字符串需要的空间，初始值为 char *s
    size = strlen(s);           // 新字符串的长度由标准字符串函数 strlen(s) 确定
    str = new char [size+1];    // 在动态存储区域开辟一块空间，用于存储初值s，包括结束符
    assert(str != '\0');        // 开辟空间不成功时，运行异常，退出
    strcpy(str, s);             // 在空间申请成功后，用标准字符串函数strcpy将s完全复制到指针str所指的存储空间
}

例如，我们可以通过上面的带参数的构造函数通过 String s1("hello"); 定义一个 String 类的变量 s1，初始值为 hello。那么我们就可以申请一个容纳下 hello 的空间来将 hello 容纳进去，并且将 size 设置成相应的大小。

String s1("hello");

private:
    char *s;
    size_t size;        // 值为5

赋值算子

String String::operator=(String& s){        // 参数s将被赋值并覆盖本串。
    if (size != s.size){                    // 比较本串和参数串s的大小：若本串和参数串长度不一致，则释
        delete [] str;                         // 放原本的串的存储空间
        str = new char [s.size+1];             // 按照参数s的大小申请新的空间，并把参数s的串值复制到本串中
        assert(str!=0);
        size=s.size;
    }
    strcpy(str, s.str);                     // 将参数串s赋值到本串
    return *this;                           // 返回得到的字符串
}

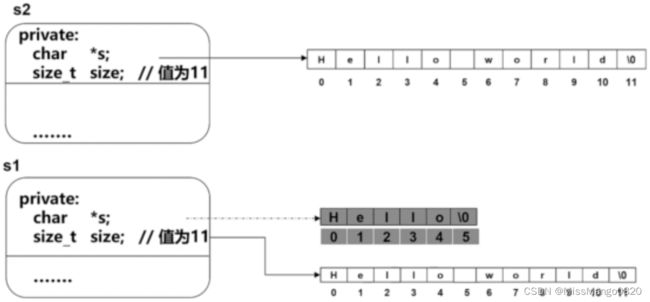
例如，我们通过构造函数构造一个串 s2，它的初值为 hello world 并通过 String s2("hello world"); s1=s2; 将这个值赋值给 s1。而 s1 此前已经被赋值 hello，所以可以看到 hello 的空间不足以存放新的值 hello world，所以将原本的空间释放掉、申请一个新的空间来容纳新值。

提取子串

// 提取子串的函数是将本串从index开始提取连续的count个字符 作为子串返回，放到temp中
String String::Substr(int index, int count){    // 取出一自下表index开始长度为count的子串返回
    int i;
    int left = size - index;                    // 本串自下标index开始到串尾的长度为left
    String temp; char *p *q;
    if (index >= size)                          // 若下标index超过本串实际串长，则返回空串；
        return temp;
    if (count > left)                           // 若count超过自index开始剩余的子串长度
        count = left;                           // 则count截取为剩余长度
    delete [] temp.str;                         // 释放原来的存储空间
    temp.str = new char [count+1];
    assert(temp.str != 0);                      // 若开辟动态存储空间失败，则退出
    p = temp.str;                               // 若指针p指向目前暂无内容的字符数组的首字符处
    q = &str[index];                            // 指针q指向本实例串的str数组的下标index字符
    for (i=0; i<count; i++)                     // 从index开始逐个提取字符到串temp中
        *p++ = *q++;
    *p = 0;                                     // 循环结束后，让temp.str的结尾为 '\0'
    temp.size = count;
    return temp;
}

例如，我们可以通过 s2 = s1.substr(6 ,5) 从串 s1 hello world 的第6个位置开始，连续提取5个字符形成子串 world 赋值给 s2。

模式匹配

概念

模式匹配（ Pattern Matching ），在目标文本 T 中寻找和定位一个给定模式 P（ Pattern ）的过程。

应用

模式匹配 有着非常广泛的应用，例如：

• 进行文本编辑时对特定词语、语句的查找；
  • 大文本（诸如，句子、段落或书本）中定位特定的模式；
  • UNIX / Linux：sed、awk、grep；
• 在生物信息方面，对DNA信息的提取；
• 用于确认是否具有某种特定形式的结构：
  • 函数式语言
• …

分类

根据匹配结果的精确性，模式匹配 可以分为 精确匹配 和 近似匹配。

精确匹配

精确匹配（ Extract String Matching ），若目标 T 中至少存在一处与模式 P 完全相同的子串，则称为匹配成功。

根据模式的不同，可以进一步的分为：

• 单选模式
  例如，Set；
• 多选模式
  例如，包含通配符的 S？t
• 正则表达式

单选模式

给定模式串 P，在目标字符串 T 中搜索与模式 P 全同的子串，简称为 配串。如果找到，则返回 T 中第一个 P 的配串的首地址。

因为模式匹配频繁用于文本的模式查找，所以效率是衡量模式匹配算法的一个重要指标。因此，存在许多种用于模式匹配的算法。

这里列出一些常用的单选模式的字符串匹配算法，包含每个算法的预处理时间和匹配时间：

朴素匹配算法

朴素 匹配算法（ Native / Brute Force ），本质上是穷举，尝试所有匹配的可能。

假设 T = t₀t₁t₂…t_n， P = p₀p₂…p_m-1。i, j 分别表示 T 和 P 当前字符的下标，在目标字符串 T 中搜索与模式 P 的配串：

1. 将模式从头与目标串的第 i 个字符开始比较：若相等，则继续逐个比较后续字符；
2. 匹配成功（ p₀ = t_k，p₁ = t_k+1，…，p_m-1 = t_k+m-1），即 T.substr(k, m) == P；
3. 若一趟匹配过程发生失配（ p_j != t_i ），则将 P 整体右移1位开始下一趟的匹配

例如，存在目标字符串 T = ababababababb 和模式串 P = abababb：

1. 将P从0开始与T的第 i 个字符开始比较：若相等，则继续逐个比较后续字符；在第6个字符发生失配（ P₆ != T₆），将P整体右移1位开始下一趟的匹配；
2. 将P从1开始与T的第 i 个字符开始比较：在第1个字符发生失配（P₀ ！= T₁ ），将P整体右移1位开始下一趟的匹配；
3. 重复上述步骤，直至 T.substr(k, m) == P 匹配成功或者匹配失败。

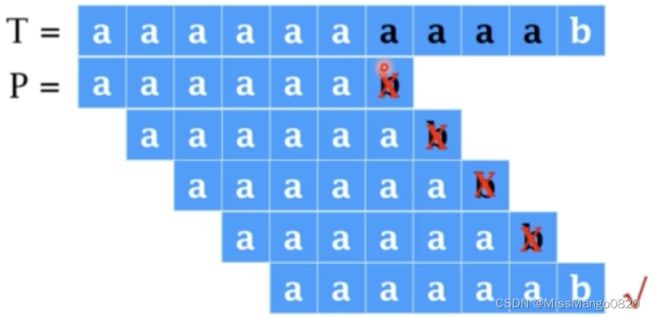
例如，存在目标字符串 T = aaaaaaaaaab 和模式串 P = aaaaaab：

1. 将P从0开始与T的第 i 个字符开始比较：若相等，则继续逐个比较后续字符；在第6个字符发生失配（ P₆ != T₆），将P整体右移1位开始下一趟的匹配；
2. 将P从1开始与T的第 i 个字符开始比较：在第1个字符发生失配（P₆ ！= T₇ ），将P整体右移1位开始下一趟的匹配；
3. 重复上述步骤，直至 T.substr(k, m) == P 匹配成功或者匹配失败。

朴素模式 的匹配算法实现如下：

int g, j;

int FindPattern(string T, string P, int startindex)
    for (int g=startindex; g<=T.length()-P.length(); g++){     // g为T的游标，用模板P和目标T的第g位置子串进行比较
        for (int j=0; ((j<P.length()) && (T[g+j]==P[j])); j++)
            ;
        if (j==P.length())
            return g;
    }
    return (-1);                                               // for循环结束，或者，startindex溢出，匹配失败
}

朴素模式 的匹配算法的时间复杂度分析如下：

• 最差情形
  
  

• 最佳情形
  
  
  

KMP 算法

Knuth - Morris - Pratt（ KMP ）发现每个字符对应的 k 值仅依赖于模式 P 本身，与目标串 T 无关。

1970年，S.A.Cook 在进行抽象机的理论研究时证明了最差情况下模式匹配可在 O（N+M） 时间内完成。
D.E.Knuth 和 V.R.Pratt 以 Cook理论为基础，构造了一种在 O（N+M） 时间内进行模式匹配的方法。
与此同时，J.H.Morris 在开发文本编辑器时为了避免检索文本时的回溯，也得到了同样的算法。

长度为m的模式P，P=p₀p₁p₂p₃…p_m-1。特征向量N表示模式P的字符分布特征，由m个特征数n_j组成 N = n₀n₁n₂n₃…n_m-1。
特征向量，简称 N向量。在很多文献中也称为 next 数组，每个特征数 n_j 对应 next 数组的一个元素。

【还是没搞懂KMP算法的思想…此处略…】

近似匹配

近似匹配（ Approximate String Matching )，若模式 P 与目标 T（或其子串）存在某种程度的相似，则称为匹配成功。

字符串相似度通常定义串变换所需基本操作数目。

字符串基本操作包括 插入、删除 和 替换 三种操作。

---

参考链接

---

1. 数据结构与算法 ↩︎

2. 详解计算机中的字、字节（Byte）、比特（bit）及它们之间的关系 ↩︎