数据结构与算法|第十三章：字符串匹配

数据结构与算法|第十三章：字符串匹配

项目环境

• jdk 1.8
• github 地址：https://github.com/huajiexiewenfeng/data-structure-algorithm
  • 本章模块：chapter09

1.字符串是什么？

本小节相关字符串定义内容取自于《重学数据结构与算法》- 公瑾

1.1 定义

字符串（string） 是由 n 个字符组成的一个有序整体（ n >= 0 ）。

例如，s = “BEIJING” ，s 代表这个串的串名，BEIJING 是串的值。字符串的逻辑结构和线性表很相似，不同之处在于字符串针对的是字符集，也就是字符串中的元素都是字符，线性表则没有这些限制。

在实际操作中，我们经常会用到一些特殊的字符串：

• 空串，指含有零个字符的串。例如，s = “”，书面中也可以直接用 Ø 表示。

• 空格串，只包含空格的串。它和空串是不一样的，空格串中是有内容的，只不过包含的是空格，且空格串中可以包含多个空格。例如，s = " "，就是包含了 3 个空格的字符串。

• 子串，串中任意连续字符组成的字符串叫作该串的子串。

• 原串通常也称为主串。例如：a = “BEI”，b = “BEIJING”，c = “BJINGEI” 。

  • 对于字符串 a 和 b 来说，由于 b 中含有字符串 a ，所以可以称 a 是 b 的子串，b 是 a 的主串；
  • 而对于 c 和 a 而言，虽然 c 中也含有 a 的全部字符，但不是连续的 “BEI” ，所以串 c 和 a 没有任何关系。

1.2 字符串相等

当要判断两个串是否相等的时候，就需要定义相等的标准了。只有两个串的串值完全相同，这两个串才相等。根据这个定义可见，即使两个字符串包含的字符完全一致，它们也不一定是相等的。例如 b = “BEIJING”，c = “BJINGEI”，则 b 和 c 并不相等。

1.3 字符串的存储结构

字符串的存储结构与线性表相同，也有顺序存储和链式存储两种。

• 字符串的顺序存储结构，是用一组地址连续的存储单元来存储串中的字符序列，一般是用定长数组来实现。有些语言会在串值后面加一个不计入串长度的结束标记符，比如 \0 来表示串值的终结。

  • Java 中 String 的实现使用的就是数组
    • private final char value[];

• 字符串的链式存储结构，与线性表是相似的，但由于串结构的特殊性（结构中的每个元素数据都是一个字符），如果也简单地将每个链结点存储为一个字符，就会造成很大的空间浪费。
  

• 一个结点可以考虑存放多个字符，如果最后一个结点未被占满时，可以使用 “#” 或其他非串值字符补全，如下图所示：
  
  在链式存储中，每个结点设置字符数量的多少，与串的长度、可以占用的存储空间以及程序实现的功能相关。

• 如果字符串中包含的数据量很大，但是可用的存储空间有限，那么就需要提高空间利用率，相应地减少结点数量。

• 而如果程序中需要大量地插入或者删除数据，如果每个节点包含的字符过多，操作字符就会变得很麻烦，为实现功能增加了障碍。

因此，串的链式存储结构除了在连接串与串操作时有一定的方便之外，总的来说，不如顺序存储灵活，在性能方面也不如顺序存储结构好。

2.字符串的基本操作

字符串和线性表的操作很相似，但由于字符串针对的是字符集，所有元素都是字符，因此字符串的基本操作与线性表有很大差别。线性表更关注的是单个元素的操作，比如增删查一个元素，而字符串中更多关注的是查找子串的位置、替换等操作。接下来我们以顺序存储为例，详细介绍一下字符串对于另一个字符串的增删查操作。

2.1 新增操作

字符串的新增操作和数组非常相似，都牵涉对插入字符串之后字符的挪移操作，所以时间复杂度是 O(n)。

例如，在字符串 s1 = “123456” 的正中间插入 s2 = “abc”，则需要让 s1 中的 “456” 向后挪移 3 个字符的位置，再让 s2 的 “abc” 插入进来。很显然，挪移的操作时间复杂度是 O(n)。不过，对于特殊的插入操作时间复杂度也可以降低为 O(1)。这就是在 s1 的最后插入 s2，也叫作字符串的连接，最终得到 “123456abc”。

2.2 删除操作

字符串的删除操作和数组同样非常相似，也可能会牵涉删除字符串后字符的挪移操作，所以时间复杂度是 O(n)。

例如，在字符串 s1 = “123456” 的正中间删除两个字符 “34”，则需要删除 “34” 并让 s1 中的 “56” 向前挪移 2 个字符的位置。很显然，挪移的操作时间复杂度是 O(n)。不过，对于特殊的插入操作时间复杂度也可以降低为 O(1)。这就是在 s1 的最后删除若干个字符，不牵涉任何字符的挪移。

2.3 查找操作

字符串的查找操作，是反映工程师对字符串理解深度的高频考点，这里需要你格外注意。

例如，字符串 s = “goodgoogle”，判断字符串 t = “google” 在 s 中是否存在。需要注意的是，如果字符串 t 的每个字符都在 s 中出现过，这并不能证明字符串 t 在 s 中出现了。当 t = “dog” 时，那么字符 “d”、“o”、“g” 都在 s 中出现过，但他们并不连在一起。

3. 子串查找（字符串匹配）

首先，我们来定义两个概念，主串和模式串。我们在字符串 A 中查找字符串 B，则 A 就是主串，B 就是模式串。我们把主串的长度记为 n，模式串长度记为 m。由于是在主串中查找模式串，因此，主串的长度肯定比模式串长，n>m。因此，字符串匹配算法的时间复杂度就是 n 和 m 的函数。

3.1 BF算法

BF算法中的 BF 是 Brute Force 的缩写，中文叫作暴力匹配算法，也叫朴素匹配算法。从名字可以看出，这种算法的字符串匹配方式很“暴力”，当然也就会比较简单、好懂，但相应的性能也不高。

作为最简单、最暴力的字符串匹配算法，BF 算法的思想可以用一句话来概括，那就是，我们在主串中，检查起始位置分别是0、1、2…n-m且长度为m的n-m+1个子串，看有没有跟模式串匹配的。

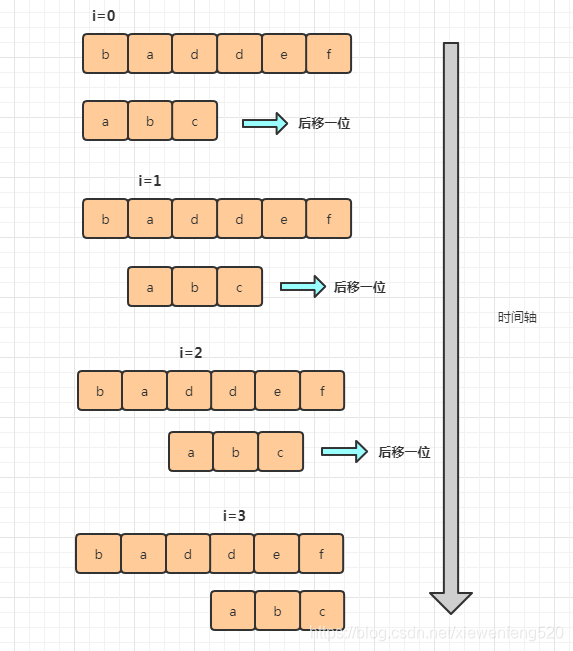
从上面的算法思想和例子，我们可以看出，在极端情况下，比如主串是“aaaaa…aaaaaa”（省略号表示有很多重复的字符a），模式串是“aaaaab”。我们每次都比

对 m 个字符，要比对 n-m+1 次，所以，这种算法的最坏情况时间复杂度是 $O(n\ast m)$。

尽管理论上，BF算法的时间复杂度很高，是 $O(n\ast m)$，但在实际的开发中，它却是一个比较常用的字符串匹配算法。为什么这么说呢？原因有两点。

• 第一，实际的软件开发中，大部分情况下，模式串和主串的长度都不会太长。而且每次模式串与主串中的子串匹配的时候，当中途遇到不能匹配的字符的时候，就可以就停止了，不需要把 m 个字符都比对一下。所以，尽管理论上的最坏情况时间复杂度是 $O(n\ast m)$，但是，统计意义上，大部分情况下，算法执行效率要比这个高很多。

• 第二，朴素字符串匹配算法思想简单，代码实现也非常简单。简单意味着不容易出错，如果有 bug 也容易暴露和修复。在工程中，在满足性能要求的前提下，简单 是首选。这也是我们常说的 KISS（Keep it Simple and Stupid）设计原则。

所以，在实际的软件开发中，绝大部分情况下，朴素的字符串匹配算法就够用了。

3.2 实现代码

    /**
     * BF算法
     *
     * @param strA 主串
     * @param strB 模式串
     * @return 模式串B所在的位置
     */
    public static int strMatchForBF(String strA, String strB) {
        char[] charsA = strA.toCharArray();
        char[] charsB = strB.toCharArray();
        int lengthA = charsA.length;
        int lengthB = charsB.length;
        for (int i = 0; i <= lengthA - lengthB; i++) {
            int k = 0;// 用来记录对比结果
            if (charsA[i] == charsB[0]) {// 如果第一位相等
                for (int j = 1; j < lengthB; j++) {
                    if (charsA[i + j] == charsB[j]) {// 后续的字符是否相等
                        k++;
                    } else {
                        break;
                    }
                }
                if (k == lengthB - 1) {
                    return i;
                }
            }
        }
        return -1;
    }

测试

    public static void main(String[] args) {
        String strA = "baddef";
        String strB = "abc";
        String strC = "ad";
        int index = strMatchForBF(strA, strB);
        int index1 = strMatchForBF(strA, strC);
        System.out.printf("主串：[%s],模式串：[%s],匹配位置：[%d]\n", strA, strB, index);
        System.out.printf("主串：[%s],模式串：[%s],匹配位置：[%d]\n", strA, strC, index1);
    }

执行结果：

主串：[baddef],模式串：[abc],匹配位置：[-1]
主串：[baddef],模式串：[ad],匹配位置：[1]

4.字符串匹配算法题

4.1 查找出两个字符串的最大公共字串

假设有且仅有 1 个最大公共子串。比如，输入 a = “badfeifgh”， b = “cadfe”。由于字符串 “adfe” 同时在 a 和 b 中出现，且是同时出现在 a 和 b 中的最长子串。因此输出 "adfe”。

解题思路

• 遍历 a 和 b，如果元素相等，继续对比后续的元素是否相等
• 需要注意的是对比后续元素，数据脚标越界问题

代码如下：

public class LongestSameSubStringSolution {
    public static void main(String[] args) {
        String a = "badfeifgh";
        String b = "cadfe";
        System.out.println(getLongestSameSubString(a, b));
    }

    public static String getLongestSameSubString(String a, String b) {
        Integer aLength = a.length();
        Integer bLength = b.length();
        String res = "";
        for (int i = 0; i < aLength; i++) {
            for (int j = 0; j < bLength; j++) {
                if (a.charAt(i) == b.charAt(j)) {// 如果相等
                    int startIndex = j;
                    for (int k = 0; k < bLength; k++) {// 继续遍历 a 和 b 后面的元素
                        if (i + k < aLength && j + k < bLength && a.charAt(i + k) == b.charAt(j + k)) {
                            String str = b.substring(startIndex, j + k + 1);
                            if (str.length() > res.length()) {
                                res = str;
                            }
                        }
                    }
                }
            }
        }
        return res;
    }
}

执行结果：

adfe

时间复杂度：

假设字符串 a 的长度为 n，字符串 b 的长度为 m，可见时间复杂度是 n 和 m 的函数。从代码结构来看，第一步需要两层的循环去查找共同出现的字符，这就是 $O(n\ast m)$。一旦找到了共同出现的字符之后，还需要再继续查找共同出现的字符串，这也就是又嵌套了一层循环。可见最终的时间复杂度是 $O(n\ast m\ast m)$，即 $O(n\ast m^2)$。

4.2 反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

示例 1：

输入：[“h”,“e”,“l”,“l”,“o”]
输出：[“o”,“l”,“l”,“e”,“h”]
示例 2：

输入：[“H”,“a”,“n”,“n”,“a”,“h”]
输出：[“h”,“a”,“n”,“n”,“a”,“H”]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-string

题解

使用前面章节讲到的递归进行实现

public class ReverseStringSolution {

    public static void main(String[] args) {
        char[] a = "hello".toCharArray();
        System.out.println("原字符串：" + Arrays.toString(a));
        reverseString(a);
        System.out.println("反转后：" + Arrays.toString(a));
    }

    public static void reverseString(char[] s) {
        reverseStr(s, 0, s.length - 1);
    }

    private static void reverseStr(char[] s, int left, int right) {
        if (left <= right) {
            char tmp = s[right];
            s[right--] = s[left];
            s[left++] = tmp;
            reverseStr(s, left, right);
        }
    }

}

执行结果：

原字符串：[h, e, l, l, o]
反转后：[o, l, l, e, h]

5.小结

字符串的逻辑结构和线性表极为相似，区别仅在于串的数据对象约束为字符集。但是，字符串的基本操作和线性表有很大差别：

• 在线性表的基本操作中，大多以“单个元素”作为操作对象

• 在字符串的基本操作中，通常以“串的整体”作为操作对象

• 字符串的增删操作和数组很像，复杂度也与之一样。但字符串的查找操作就复杂多了

6.参考

• 《重学数据结构与算法》- 公瑾
• 《数据结构与算法之美》- 王争