感知机算法的python实现
算法原理
这是《统计学习方法》对感知机算法原理的描述:

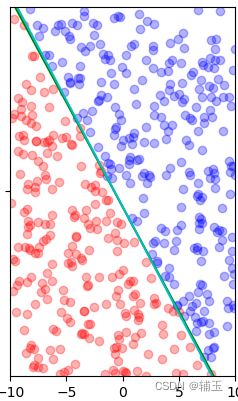
为简化问题难度,本文只讨论二维平面上点的线性可分。我们可以不用理会“超平面”这个概念的原意。在这个前提下,感知机要解决的问题是给出一条直线,将二维平面上的正实例点和负实例点线性分开,参照下图(蓝色为正实例点,红色为负实例点)。
可将算法逻辑表述如下:
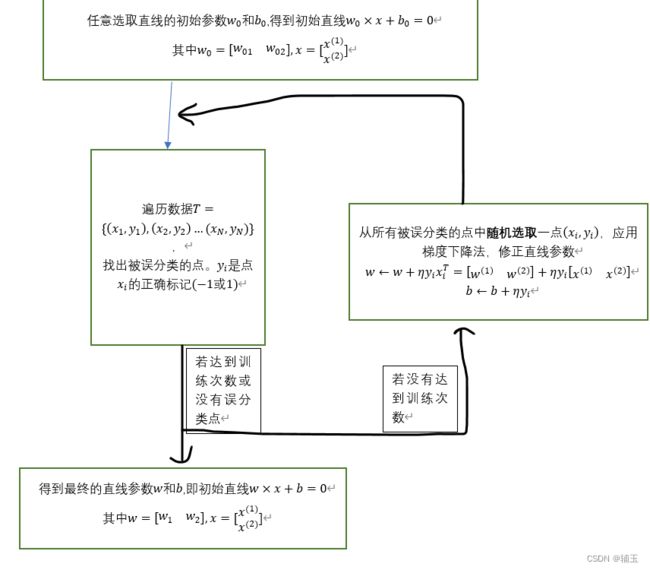
因为手头没有可以使用的现成数据,我们可以随机生成一些点并将其提前分好类,然后再训练这些点,得到分类直线wx+b=0。
完整代码及分块剖析
总体逻辑
分块剖析
# 导入数据包
import numpy as np #numpy为开源的python科学计算扩展库,用于处理任意维度数组和矩阵
import matplotlib.pyplot as plt #matplotlib库用于数据可视化,即画图
import random #导入随机数模块
from typing import List,Tuple
"""
import A as B 意为为简化命名,给A起了个别名B
typing模块的作用:类型检查,防止运行时出现参数和返回值类型不符合
List(列表)为python的基本数据结构,其中每个元素都被分配一个数字,这个数字就是它的位置或索引
Tuple(元组)为特殊的有序列表,它一旦被创建完,其对每个元素的指引不能被修改
"""
#定义随机点的生成函数
def sample_point(w:float,b:float,num:int)->Tuple[List[List[float]],List[float]]:
x, y=[], [] #x和y是列表
for _ in range(num): #若在循环体中不需要用到自定义变量,可将自定义变量写为下划线‘_’
p_x1 = np.random.random_sample(1) * 20 - 10
p_x2 = np.random.random_sample(1) * 20 - 10
if w*p_x1+b-p_x2>0: #若某点在理想直线上方
p_y=1 #将该点标记为正实例点
else:
p_y=-1 #否则将该点标记为负实例点
x.append([p_x1, p_x2]) #python允许列表的单个元素为列表
y.append(p_y)
return x, y
"""
:是参数的类型建议符,>是函数返回值的类型建议符,两者作用是标注参数和函数返回值类型,降代码阅读难度
numpy.random.random_sample()是生成一个[0,1)之间随机浮点数或N维浮点数组
"""
#随机生成一条直线,将该直线作为理想直线
w_ideal = np.random.random_sample(1)*10-5 #w_ideal范围在[-5,5]
b_ideal = np.random.random_sample(1)*10-5 #b_ideal范围在[-5,5]
x = np.linspace(-10, 10, 800) #linspace(s,e,n)从[s,e]内生成一个含有n个值的序列
line_ideal = w_ideal*x + b_ideal #绘制理想直线
#随机生成一些点,根据直线将这些点划分为2个区域
sample_x, sample_y = sample_point(w_ideal, b_ideal, 500) #随机生成500个点
#感知机函数
def perceptron(x, y, learning_rate, t)->Tuple[np.ndarray, List[int]]:
#初始化参数
theta = np.zeros((3,1))#生成一个2行1列的数组
error_list =[]#定义一个列表存储每次优化前误分类点的个数
#开始训练
for _ in range(t): #训练t次
error_count = 0 #每次训练开始时误分类点个数为0
error_index = [] #定义一个列表存储每个误分类点的索引以供后面随机选取
for i, x_i in enumerate(x): #遍历列表x
y_i = theta[0] * x_i[0]+theta[1] * x_i[1]+theta[2]
if y_i * y[i] <= 0: #若某点被分类错误
error_index.append(i) #将该点索引存入相应列表
error_count += 1 #误分类点个数加1
error_list.append(error_count) #将该次优化前误分类点个数存入error_list列表
if error_count > 0: #若有误分类点
i = random.choice(error_index) #则从误分类点列表中随机选取一点进行优化
theta[0] += learning_rate * y[i] * x[i][0]
theta[1] += learning_rate * y[i] * x[i][1]
theta[2] += learning_rate * y[i] * 1
return theta, error_list
"""
x是存储了每点坐标的列表,y是存储每点理想输出的列表,learning_rate为学习率,t为训练次数
ndarray为多维数组,List[int]表示List里的元素为int类型
函数perceptron返回的值是训练完成后得到的最终参数、每次优化前误分类点的个数
"""
#调用感知机进行训练
theta, error_list = perceptron(sample_x, sample_y, 0.5, 100)
#数据可视化
#先画训练前得到的随机点图和理想直线
plt.subplot(121) #将整个窗口分为1行2列,当前位置1
plt.xlim([-10,10]) #绘图的x轴范围在[-10,10]
plt.ylim([-10,10])
plt.plot(x,line_ideal, 'g', 'linewidth=10')
for i,p_x in enumerate(sample_x): #enumerate函数在遍历一个序列时,可同时得到每个元素和其索引
if sample_y[i] == 1:
plt.scatter(p_x[0], p_x[1], c='r', alpha=0.3)
else:
plt.scatter(p_x[0], p_x[1], c='b', alpha=0.3)
#求解训练完成后得到的参数
w_best = -theta[0] / theta[1]
b_best = -theta[2] / theta[1]
y_best = w_best * x + b_best #计算得到的直线的每点纵坐标
plt.plot(x, y_best, 'c', 'linewidth=10') #绘制得到的直线时,使用不同的颜色以便区分
plt.show()
完整代码
# 导入数据包
import numpy as np #numpy为开源的python科学计算扩展库,用于处理任意维度数组和矩阵
import matplotlib.pyplot as plt #matplotlib库用于数据可视化,即画图
import random #导入随机数模块
from typing import List,Tuple
"""
import A as B 意为为简化命名,给A起了个别名B
typing模块的作用:类型检查,防止运行时出现参数和返回值类型不符合
List(列表)为python的基本数据结构,其中每个元素都被分配一个数字,这个数字就是它的位置或索引
Tuple(元组)为特殊的有序列表,它一旦被创建完,其对每个元素的指引不能被修改
"""
#定义随机点的生成函数
def sample_point(w:float,b:float,num:int)->Tuple[List[List[float]],List[float]]:
x, y=[], [] #x和y是列表
for _ in range(num): #若在循环体中不需要用到自定义变量,可将自定义变量写为下划线‘_’
p_x1 = np.random.random_sample(1) * 20 - 10
p_x2 = np.random.random_sample(1) * 20 - 10
if w*p_x1+b-p_x2>0: #若某点在理想直线上方
p_y=1 #将该点标记为正实例点
else:
p_y=-1 #否则将该点标记为负实例点
x.append([p_x1, p_x2]) #python允许列表的单个元素为列表
y.append(p_y)
return x, y
"""
:是参数的类型建议符,>是函数返回值的类型建议符,两者作用是标注参数和函数返回值类型,降代码阅读难度
numpy.random.random_sample()是生成一个[0,1)之间随机浮点数或N维浮点数组
"""
#感知机函数
def perceptron(x, y, learning_rate, t)->Tuple[np.ndarray, List[int]]:
#初始化参数
theta = np.zeros((3,1))#生成一个2行1列的数组
error_list =[]#定义一个列表存储每次优化前误分类点的个数
#开始训练
for _ in range(t): #训练t次
error_count = 0 #每次训练开始时误分类点个数为0
error_index = [] #定义一个列表存储每个误分类点的索引以供后面随机选取
for i, x_i in enumerate(x): #遍历列表x
y_i = theta[0] * x_i[0]+theta[1] * x_i[1]+theta[2]
if y_i * y[i] <= 0: #若某点被分类错误
error_index.append(i) #将该点索引存入相应列表
error_count += 1 #误分类点个数加1
error_list.append(error_count) #将该次优化前误分类点个数存入error_list列表
if error_count > 0: #若有误分类点
i = random.choice(error_index) #则从误分类点列表中随机选取一点进行优化
theta[0] += learning_rate * y[i] * x[i][0]
theta[1] += learning_rate * y[i] * x[i][1]
theta[2] += learning_rate * y[i] * 1
return theta, error_list
"""
x是存储了每点坐标的列表,y是存储每点理想输出的列表,learning_rate为学习率,t为训练次数
ndarray为多维数组,List[int]表示List里的元素为int类型
函数perceptron返回的值是训练完成后得到的最终参数、每次优化前误分类点的个数
"""
#随机生成一条直线,将该直线作为理想直线
w_ideal = np.random.random_sample(1)*10-5 #w_ideal范围在[-5,5]
b_ideal = np.random.random_sample(1)*10-5 #b_ideal范围在[-5,5]
x = np.linspace(-10, 10, 800) #linspace(s,e,n)从[s,e]内生成一个含有n个值的序列
line_ideal = w_ideal*x + b_ideal #绘制理想直线
#随机生成一些点,根据直线将这些点划分为2个区域
sample_x, sample_y = sample_point(w_ideal, b_ideal, 500) #随机生成500个点
#调用感知机进行训练
theta, error_list = perceptron(sample_x, sample_y, 0.5, 100)
#数据可视化
#先画训练前得到的随机点图和理想直线
plt.subplot(121) #将整个窗口分为1行2列,当前位置1
plt.xlim([-10,10]) #绘图的x轴范围在[-10,10]
plt.ylim([-10,10])
plt.plot(x,line_ideal, 'g', 'linewidth=10')
for i,p_x in enumerate(sample_x): #enumerate函数在遍历一个序列时,可同时得到每个元素和其索引
if sample_y[i] == 1:
plt.scatter(p_x[0], p_x[1], c='r', alpha=0.3)
else:
plt.scatter(p_x[0], p_x[1], c='b', alpha=0.3)
#求解训练完成后得到的参数
w_best = -theta[0] / theta[1]
b_best = -theta[2] / theta[1]
y_best = w_best * x + b_best #计算得到的直线的每点纵坐标
plt.plot(x, y_best, 'c', 'linewidth=10') #绘制得到的直线时,使用不同的颜色以便区分
plt.show()




