Java实现二叉树的遍历(先序、中序和后序)
一、实验目的
1、掌握二叉树的特点及其存储方式;
2、掌握二叉树的创建;
3、掌握二叉树先序、中序、后序遍历的基本方法及应用;
4、掌握判断二叉树是否是完全二叉树的方法。
二、实验内容
1、用先序方法建立一棵二叉树;
2、实现输出二叉树先序、中序和后序遍历序列中第k个数据元素的操作;
3、实现判断二叉树是否是完全二叉树的操作。
三、实验步骤
1、二叉链表结点类的定义;
2、二叉树类的定义;
3、创建一棵二叉树;
4、实现输出以上二叉树先序、中序和后序遍历序列中第k个数据元素的操作;
5、判断二叉树是否是完全二叉树;
四、代码及运行结果
import java.util.*;
public class BiTree {
private BiTreeNode root;
public BiTree() {
this.root = null;
}
public BiTree(BiTreeNode root) {
this.root = root;
}
/*
public BiTree(String preOrder, String inOrder, int preIndex, int inIndex, int count) {
if (count > 0) {
char r = preOrder.charAt(preIndex);
int i = 0;
for (; i < count; i++)
if (r == inOrder.charAt(i + inIndex))
break;
root = new BiTreeNode(r);
root.lchild = new BiTree(preOrder, inOrder, preIndex + 1, inIndex, i).root;
root.rchild = new BiTree(preOrder, inOrder, preIndex + i + 1, inIndex + i + 1, count - i - 1).root;
}
}
*/
private static int index=0;
public BiTree(String preStr){
char c=preStr.charAt(index++);
if (c!='#'){
root=new BiTreeNode(c);
root.lchild=new BiTree(preStr).root;
root.rchild=new BiTree(preStr).root;
}
else {
root=null;
}
}
public Link preRootTraverse(){
Link l1=new Link();
Link link;
link=preRootTraverse(l1,root);
return link;
}
private Link preRootTraverse(Link link,BiTreeNode T){
if (T!=null){
try {
link.insert(link.length(), T.data);
} catch (Exception e) {
e.printStackTrace();
}
preRootTraverse(link,T.lchild);
preRootTraverse(link,T.rchild);
}
return link;
}
public Link inRootTraverse(){
Link l1=new Link();
Link link;
link=inRootTraverse(l1,root);
return link;
}
private Link inRootTraverse(Link link,BiTreeNode T){
if (T!=null){
inRootTraverse(link,T.lchild);
try {
link.insert(link.length(), T.data);
} catch (Exception e) {
e.printStackTrace();
}
inRootTraverse(link,T.rchild);
}
return link;
}
public Link postRootTraverse(){
Link l1=new Link();
Link link;
link=postRootTraverse(l1,root);
return link;
}
private Link postRootTraverse(Link link,BiTreeNode T){
if (T!=null){
postRootTraverse(link,T.lchild);
postRootTraverse(link,T.rchild);
try {
link.insert(link.length(), T.data);
} catch (Exception e) {
e.printStackTrace();
}
}
return link;
}
public boolean isCompleteBinaryTree(){
isCompleteBinaryTree(root);
return isCompleteBinaryTree(root);
}
private boolean isCompleteBinaryTree(BiTreeNode t) {
if (t == null) {
return true;
}
// 从当前节点开始,后面的节点是否都需要是叶子节点
boolean isLeafNode = false;
LinkedList queue = new LinkedList<>();
queue.offer(t);
// 宽度优先遍历二叉树
while (!queue.isEmpty()) {
BiTreeNode node = queue.poll();
// ①、左孩子为空,右孩子不为空的情况,直接返回false
if (node.rchild != null && node.lchild == null) {
return false;
}
// ②、如果后面的节点都应该是叶子节点,但是又有左孩子或右孩子,则直接返回false
if (isLeafNode && (node.lchild != null || node.rchild != null)) {
return false;
}
// ③、遇到第一个左右孩子不双全的节点,那么该节点后的所有节点都应该是叶子节点
if (node.lchild == null || node.rchild == null) {
isLeafNode = true;
}
// 压入左孩子到队列
if (node.lchild != null) {
queue.offer(node.lchild);
}
// 压入右孩子到队列
if (node.rchild != null) {
queue.offer(node.rchild);
}
}
// 其余情况都返回true
return true;
}
/*
public boolean isCompleteBinaryTree(){
isCompleteBinaryTree(root);
return isCompleteBinaryTree(root);
}
private boolean isCompleteBinaryTree(BiTreeNode t)
{
if(t==null){
return true;
}
LinkQueue q=new LinkQueue<>();
q.offer(t);
boolean isLeafOrLeft=false;
while(!q.isEmpty()){
BiTreeNode cur=q.poll();
if (isLeafOrLeft){
if (cur.lchild!=null||cur.rchild!=null){
return false;
}
}
else {
if(cur.lchild!=null &&cur.rchild!=null){//左右孩子都有
q.offer(cur.lchild);
q.offer(cur.rchild);
} else if(cur.lchild!=null){//只有左孩子
q.offer(cur.lchild);
isLeafOrLeft=true;
} else if(cur.rchild!=null){//只有右孩子
return false;
} else{//叶子结点
isLeafOrLeft=true;
}
}
}
return true;
}
*/
} public class BiTreeNode {
public Object data;
public BiTreeNode lchild,rchild;
public BiTreeNode(){
this(null);
}
public BiTreeNode(Object data){
this(data,null,null);
}
public BiTreeNode(Object data,BiTreeNode lchild,BiTreeNode rchild){
this.data=data;
this.lchild=lchild;
this.rchild=rchild;
}
}public class Link {
public Node head;
public Link() {
head = new Node();
}
public Object get(int i)throws Exception{
Node p=head.next;
int j=0;
while (p!=null&&ji||p==null){
throw new Exception("第i个元素不存在");
}
return p.data;
}
public void insert(int i, Object x) throws Exception {
Node p = head;
int j = -1;
while (p != null && j < i - 1) {
p = p.next;
++j;
}
if (j > i - 1 || p == null) {
throw new Exception("插入位置不合法");
}
Node s = new Node(x);
s.next = p.next;
p.next = s;
}
public void display() {
Node node = head.next;
while (node != null) {
System.out.print(node.data + " ");
node = node.next;
}
System.out.println();
}
public int length() {
Node p = head.next;
int length = 0;
while (p != null) {
p = p.next;
++length;
}
return length;
}
} public class Node{
public Object data;
public Node next;
public Node(){
this(null,null);
}
public Node (Object data){
this(data,null);
}
public Node(Object data,Node next){
this.data=data;
this.next=next;
}
}import java.util.Scanner;
public class Test {
public static void main(String[] args){
/*
String preOrder="ABCDFGE";
String inOrder="BAFDGCE";
BiTree T=new BiTree(preOrder,inOrder,0,0,preOrder.length());
*/
System.out.println("输入标明空子树的先序遍历序列以建立一个二叉树");
Scanner scanner=new Scanner(System.in);
String preStr=scanner.next();
BiTree T=new BiTree(preStr);
System.out.println("该二叉树的先序遍历序列是:");
Link l1;
l1=T.preRootTraverse();
l1.display();
System.out.println("该二叉树的中序遍历序列是:");
Link l2;
l2=T.inRootTraverse();
l2.display();
System.out.println("该二叉树的后序遍历序列是:");
Link l3;
l3=T.postRootTraverse();
l3.display();
System.out.println("输入想查找的二叉树先序遍历序列中第k个数据元素");
Scanner sc = new Scanner(System.in);
int k= sc.nextInt();
try {
System.out.println("二叉树先序遍历序列中第"+k+"个数据元素"+l1.get(k-1));
} catch (Exception e) {
e.printStackTrace();
}
try {
System.out.println("二叉树中序遍历序列中第"+k+"个数据元素"+l2.get(k-1));
} catch (Exception e) {
e.printStackTrace();
}
try {
System.out.println("二叉树后序遍历序列中第"+k+"个数据元素"+l3.get(k-1));
} catch (Exception e) {
e.printStackTrace();
}
boolean is=T.isCompleteBinaryTree();
if (is){
System.out.println("是完全二叉树");
}
else {
System.out.println("不是完全二叉树");
}
}
}
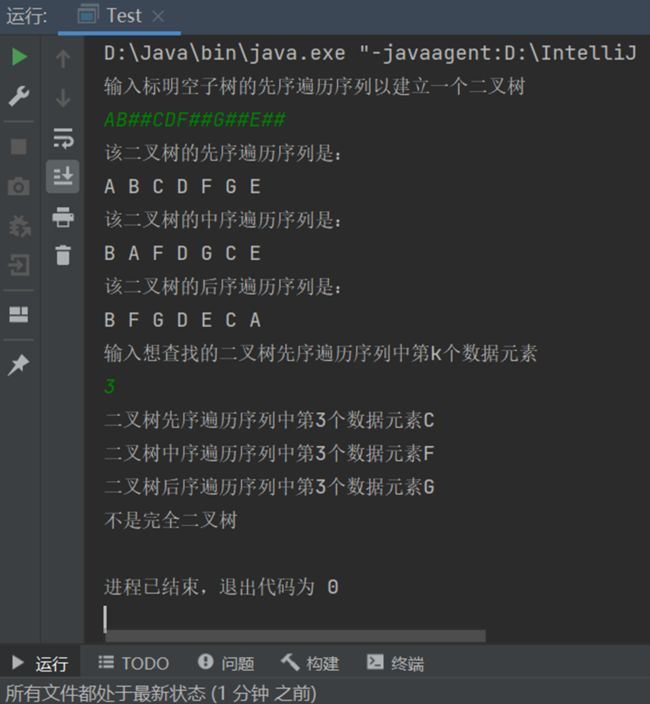
运行结果:
五、问题讨论
1、先序、中序、后序遍历二叉树的区别?
访问根结点及遍历左子树和右子树的先后次序不同。先根遍历是指每次进入一层递归调用时先访问根结点,然后依次对它的左、右子树执行递归进行调用;中根遍历是指在执行完左子树的递归调用后再访问根节点,然后对右子树执行递归调用;后根遍历则是指执行完左、右子树的递归调用后,最后访问根结点。
2、完全二叉树的特点是什么?
一棵具有n个结点的二叉树,它的逻辑结构与满二叉树的前n个结点的逻辑结构相同。