Codeforces Round 886 (Div. 4)

目录

A. To My Critics

B. Ten Words of Wisdom

C. Word on the Paper

D. Balanced Round

E. Cardboard for Pictures

F. We Were Both Children

G. The Morning Star

---

A. To My Critics

                                                        time limit per test1 second
                                                memory limit per test256 megabytes
                                                        inputstandard input
                                                        outputstandard output
Suneet has three digits a, b, and c.

Since math isn't his strongest point, he asks you to determine if you can choose any two digits to make a sum greater or equal to 10.

Output "YES" if there is such a pair, and "NO" otherwise.

Input
The first line contains a single integer tt (1≤t≤1000) — the number of test cases.

The only line of each test case contains three digits a, b, c (0≤a,b,c≤9).

Output

For each test case, output "YES" if such a pair exists, and "NO" otherwise.

You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).

Example

input

5
8 1 2
4 4 5
9 9 9
0 0 0
8 5 3

output

YES
NO
YES
NO
YES

Note

For the first test case, by choosing the digits 8 and 2 we can obtain a sum of 8+2=10 which satisfies the condition, thus the output should be "YES".

For the second test case, any combination of chosen digits won't be at least 1010, thus the output should be "NO" (note that we can not choose the digit on the same position twice).

For the third test case, any combination of chosen digits will have a sum equal to 1818, thus the output should be "YES".

思路

排序求两个最大的和是否大于10.

#include
#define int long long
using namespace std;
const int N=5;
int a[N];
int t;

void solve()
{
	int n=3;
	for(int i=0;i>a[i];
	sort(a,a+n);
	if(a[2]+a[1]>=10) puts("YES");
	else puts("NO");
}

signed main()
{
	cin>>t;
	while(t--) solve();
	return 0;
}

B. Ten Words of Wisdom

                                        time limit per test1 second
                                memory limit per test256 megabytes
                                                inputstandard input
                                                outputstandard output
In the game show "Ten Words of Wisdom", there are nn participants numbered from 11 to nn, each of whom submits one response. The ii-th response is aiai words long and has quality bibi. No two responses have the same quality, and at least one response has length at most 1010.

The winner of the show is the response which has the highest quality out of all responses that are not longer than 1010 words. Which response is the winner?

Input

The first line contains a single integer tt (1≤t≤1001≤t≤100) — the number of test cases.

The first line of each test case contains a single integer nn (1≤n≤501≤n≤50) — the number of responses.

Then nn lines follow, the ii-th of which contains two integers aiai and bibi (1≤ai,bi≤50) — the number of words and the quality of the ii-th response, respectively.

Additional constraints on the input: in each test case, at least one value of ii satisfies ai≤10ai≤10, and all values of bibi are distinct.

Output

For each test case, output a single line containing one integer x (1≤x≤n) — the winner of the show, according to the rules given in the statement.

It can be shown that, according to the constraints in the statement, exactly one winner exists for each test case.

Example

input

3
5
7 2
12 5
9 3
9 4
10 1
3
1 2
3 4
5 6
1
1 43

output

4
3
1

Note

In the first test case, the responses provided are as follows:

Response 1: 7 words, quality 2
Response 2: 12 words, quality 5
Response 3: 9 words, quality 3
Response 4: 9 words, quality 4
Response 5: 10 words, quality 1
We can see that the responses with indices 1, 3, 4, and 5 have lengths not exceeding 10 words. Out of these responses, the winner is the one with the highest quality.

Comparing the qualities, we find that:

Response 1 has quality 2.
Response 3 has quality 3.
Response 4 has quality 4.
Response 5 has quality 1.
Among these responses, Response 4 has the highest quality.

思路

求所有a<=10条件下b最大的编号。

#include
#define int long long
using namespace std;
int t;
int n;

void solve()
{
	cin>>n;
	int id=0,ans=-2e9;
	for(int i=1;i<=n;i++) 
	{
		int x,y;
		cin>>x>>y;
		if(x<=10&&ans>t;
	while(t--) solve();
	return 0;
}

C. Word on the Paper

                                                        time limit per test1 second
                                                memory limit per test256 megabytes
                                                                inputstandard input
                                                                outputstandard output
On an 8×8 grid of dots, a word consisting of lowercase Latin letters is written vertically in one column, from top to bottom. What is it?

Input

The input consists of multiple test cases. The first line of the input contains a single integer t (1≤t≤1000) — the number of test cases.

Each test case consists of 8 lines, each containing 8 characters. Each character in the grid is either . (representing a dot) or a lowercase Latin letter (a–z).

The word lies entirely in a single column and is continuous from the beginning to the ending (without gaps). See the sample input for better understanding.

Output

For each test case, output a single line containing the word made up of lowercase Latin letters (a–z) that is written vertically in one column from top to bottom.

Example

input

5
........
........
........
........
...i....
........
........
........
........
.l......
.o......
.s......
.t......
........
........
........
........
........
........
........
......t.
......h.
......e.
........
........
........
........
........
.......g
.......a
.......m
.......e
a.......
a.......
a.......
a.......
a.......
a.......
a.......
a.......

output

i
lost
the
game
aaaaaaaa

思路

遍历二维数组求所有小写字母构成的字符串。

#include
#define int long long
using namespace std;
const int N=55;
int a[N],b[N],c[N];
int t;
int n;

void solve()
{
	n=8;
	string ans;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			char x;
			cin>>x;
			if(x!='.') ans+=x;
		}
	cout<>t;
	while(t--) solve();
	return 0;
}

D. Balanced Round

                                        time limit per test2 seconds
                                memory limit per test256 megabytes
                                                inputstandard input
                                                outputstandard output
You are the author of a Codeforces round and have prepared nn problems you are going to set, problem ii having difficulty aiai. You will do the following process:

remove some (possibly zero) problems from the list;
rearrange the remaining problems in any order you wish.
A round is considered balanced if and only if the absolute difference between the difficulty of any two consecutive problems is at most k (less or equal than k).

What is the minimum number of problems you have to remove so that an arrangement of problems is balanced?

Input

The first line contains a single integer tt (1≤t≤1000) — the number of test cases.

The first line of each test case contains two positive integers nn (1≤n≤2⋅10^5) and kk (1≤k≤10^9) — the number of problems, and the maximum allowed absolute difference between consecutive problems.

The second line of each test case contains nn space-separated integers aiai (1≤ai≤10^9) — the difficulty of each problem.

Note that the sum of nn over all test cases doesn't exceed 2⋅10^5.

Output

For each test case, output a single integer — the minimum number of problems you have to remove so that an arrangement of problems is balanced.

Example

input

7
5 1
1 2 4 5 6
1 2
10
8 3
17 3 1 20 12 5 17 12
4 2
2 4 6 8
5 3
2 3 19 10 8
3 4
1 10 5
8 1
8 3 1 4 5 10 7 3

output

2
0
5
0
3
1
4

Note

For the first test case, we can remove the first 2 problems and construct a set using problems with the difficulties [4,5,6], with difficulties between adjacent problems equal to |5−4|=1≤1 and |6−5|=1≤1.

For the second test case, we can take the single problem and compose a round using the problem with difficulty 10.

思路

排好序后求最长连续之间的差值d(d<=k),然后n减去这个长度就是要求的值，

#include
#define int long long
using namespace std;
const int N=2e5+10;
int a[N],b[N],c[N];
int t;
int n;
int k;

void solve()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	sort(a+1,a+n+1);
	int cnt=1;
	vector v;
	for(int i=2;i<=n;i++)
	{
		int d=a[i]-a[i-1];
		if(d<=k) cnt++;
		else
		{
			v.push_back(cnt);
			cnt=1;
		}
	}
	if(cnt) v.push_back(cnt);
	sort(v.begin(),v.end());
	cout<>t;
	while(t--) solve();
	return 0;
}

E. Cardboard for Pictures

                                                time limit per test2 seconds
                                        memory limit per test256 megabytes
                                                        inputstandard input
                                                        outputstandard output
Mircea has nn pictures. The i-th picture is a square with a side length of sisi centimeters.

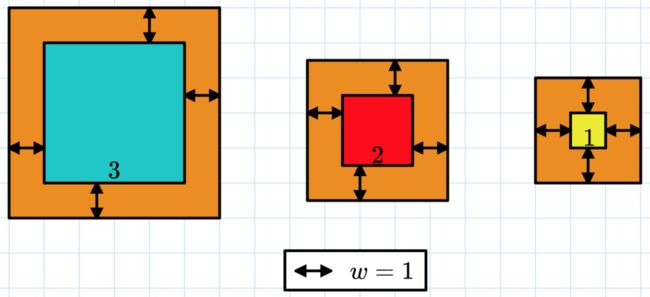
He mounted each picture on a square piece of cardboard so that each picture has a border of ww centimeters of cardboard on all sides. In total, he used cc square centimeters of cardboard. Given the picture sizes and the value cc, can you find the value of w?

A picture of the first test case. Here c=50=52+42+32, so w=1 is the answer.
Please note that the piece of cardboard goes behind each picture, not just the border.

Input

The first line contains a single integer t (1≤t≤1000) — the number of test cases.

The first line of each test case contains two positive integers nn (1≤n≤2⋅10^5) and cc (1≤c≤10^18) — the number of paintings, and the amount of used square centimeters of cardboard.

The second line of each test case contains nn space-separated integers sisi (1≤si≤10^4) — the sizes of the paintings.

The sum of nn over all test cases doesn't exceed 2⋅10^5.

Additional constraint on the input: Such an integer ww exists for each test case.

Please note, that some of the input for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).

Output

For each test case, output a single integer — the value of ww (w≥1w≥1) which was used to use exactly cc squared centimeters of cardboard.

Example
input

10
3 50
3 2 1
1 100
6
5 500
2 2 2 2 2
2 365
3 4
2 469077255466389
10000 2023
10 635472106413848880
9181 4243 7777 1859 2017 4397 14 9390 2245 7225
7 176345687772781240
9202 9407 9229 6257 7743 5738 7966
14 865563946464579627
3654 5483 1657 7571 1639 9815 122 9468 3079 2666 5498 4540 7861 5384
19 977162053008871403
9169 9520 9209 9013 9300 9843 9933 9454 9960 9167 9964 9701 9251 9404 9462 9277 9661 9164 9161
18 886531871815571953
2609 10 5098 9591 949 8485 6385 4586 1064 5412 6564 8460 2245 6552 5089 8353 3803 3764

output

1
2
4
5
7654321
126040443
79356352
124321725
113385729
110961227

Note

The first test case is explained in the statement.

For the second test case, the chosen ww was 22, thus the only cardboard covers an area of c=(2⋅2+6)2=102=100 squared centimeters.

For the third test case, the chosen ww was 44, which obtains the covered area c=(2⋅4+2)2×5=102×5=100×5=500 squared centimeters.

 思路

二分出满足条件的值。

#include
#define int long long
using namespace std;
const int N=2e5+10;
int s[N];
int t;
int n,c;
int k;

bool check(int mid)
{
	int cnt=0;
	for(int i=1;i<=n;i++)
	{
		cnt+=(2*mid+s[i])*(2*mid+s[i]);
		if(cnt>=c) return true;
	}
	return false;
}

void solve()
{
	memset(s,0,sizeof s);
	cin>>n>>c;
	for(int i=1;i<=n;i++) cin>>s[i];

	bool flag=false;
	int l=1,r=1e9;
	while(l>1;
		if(check(mid)) r=mid;
		else l=mid+1;
	}
	cout<>t;
	while(t--) solve();
	return 0;
}

F. We Were Both Children

                                                        time limit per test3 seconds
                                                memory limit per test256 megabytes
                                                                inputstandard input
                                                                outputstandard output
Mihai and Slavic were looking at a group of nn frogs, numbered from 1 to n, all initially located at point 0. Frog ii has a hop length of aiai.

Each second, frog ii hops aiai units forward. Before any frogs start hopping, Slavic and Mihai can place exactly one trap in a coordinate in order to catch all frogs that will ever pass through the corresponding coordinate.

However, the children can't go far away from their home so they can only place a trap in the first nn points (that is, in a point with a coordinate between 11 and nn) and the children can't place a trap in point 00 since they are scared of frogs.

Can you help Slavic and Mihai find out what is the maximum number of frogs they can catch using a trap?

Input

The first line of the input contains a single integer tt (1≤t≤100) — the number of test cases. The description of test cases follows.

The first line of each test case contains a single integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of frogs, which equals the distance Slavic and Mihai can travel to place a trap.

The second line of each test case contains nn integers a1,…,an (1≤ai≤10^9) — the lengths of the hops of the corresponding frogs.

It is guaranteed that the sum of nn over all test cases does not exceed 2⋅10^5.

Output

For each test case output a single integer — the maximum number of frogs Slavic and Mihai can catch using a trap.

Example

input

7
5
1 2 3 4 5
3
2 2 2
6
3 1 3 4 9 10
9
1 3 2 4 2 3 7 8 5
1
10
8
7 11 6 8 12 4 4 8
10
9 11 9 12 1 7 2 5 8 10

output

3
3
3
5
0
4
4

Note

In the first test case, the frogs will hop as follows:

Frog 1: 0→1→2→3→4→⋯
Frog 2: 0→2→4→6→8→⋯
Frog 3: 0→3→6→9→12→⋯
Frog 4: 0→4→8→12→16→⋯
Frog 5: 0→5→10→15→20→⋯
Therefore, if Slavic and Mihai put a trap at coordinate 4, they can catch three frogs: frogs 1, 2, and 4. It can be proven that they can't catch any more frogs.
In the second test case, Slavic and Mihai can put a trap at coordinate 2 and catch all three frogs instantly.

思路

遍历以i为约数开始的所有a数列中出现的最多的值。

#include
#define int long long
using namespace std;
const int N=2e5+10;
int a[N],c[N];
int t;
int n;
int k;

void solve() {
    cin >> n;
    vector cnt(n + 1, 0), mx(n + 1, 0);
    for(int i = 0; i < n; ++i) 
	{
        int x; cin >> x;
        if(x <= n) ++cnt[x];
    }
    for(int i = 1; i <= n; ++i) 
	{
        for(int j = i; j <= n; j += i) 
			mx[j] += cnt[i];
    }
    cout << *max_element(mx.begin(),mx.end()) << "\n";
}

signed main()
{
	cin>>t;
	while(t--) solve();
	return 0;
}

G. The Morning Star

                                                time limit per test2 seconds
                                        memory limit per test256 megabytes
                                                        inputstandard input
                                                        outputstandard output
A compass points directly toward the morning star. It can only point in one of eight directions: the four cardinal directions (N, S, E, W) or some combination (NW, NE, SW, SE). Otherwise, it will break.

The directions the compass can point.
There are nn distinct points with integer coordinates on a plane. How many ways can you put a compass at one point and the morning star at another so that the compass does not break?

Input
Each test contains multiple test cases. The first line contains the number of test cases tt (1≤t≤10^4). The description of the test cases follows.

The first line of each test case contains a single integer n (2≤n≤2⋅10^5) — the number of points.

Then n lines follow, each line containing two integers xi, yi(−10^9≤xi,yi≤10^9) — the coordinates of each point, all points have distinct coordinates.

It is guaranteed that the sum of nn over all test cases doesn't exceed 2⋅10^5.

Output

For each test case, output a single integer — the number of pairs of points that don't break the compass.

Example

input

5
3
0 0
-1 -1
1 1
4
4 5
5 7
6 9
10 13
3
-1000000000 1000000000
0 0
1000000000 -1000000000
5
0 0
2 2
-1 5
-1 10
2 11
3
0 0
-1 2
1 -2

output

6
2
6
8
0
Note
In the first test case, any pair of points won't break the compass:

The compass is at (0,0), the morning star is at (−1,−1): the compass will point SW.
The compass is at (0,0), the morning star is at (1,1): the compass will point NE.
The compass is at (−1,−1), the morning star is at (0,0): the compass will point NE.
The compass is at (−1,−1), the morning star is at (1,1): the compass will point NE.
The compass is at (1,1), the morning star is at (0,0): the compass will point SW.
The compass is at (1,1), the morning star is at (−1,−1): the compass will point SW.
In the second test case, only two pairs of points won't break the compass:

The compass is at (6,9), the morning star is at (10,13): the compass will point NE.
The compass is at (10,13), the morning star is at (6,9): the compass will point SW.

 思路

求4个方向的斜率中的值。

#include
#define int long long
using namespace std;
int t,n;

void solve() 
{
	map up,side,diag1,diag2; 
	cin>>n;
	while(n--)
	{
		int x,y;
		cin>>x>>y;
		up[x]++;
		side[y]++;
		diag1[x-y]++;
		diag2[x+y]++;
	}
	int ans=0;
	for(auto it:up) ans+=it.second*(it.second-1);
	for(auto it:side) ans+=it.second*(it.second-1);
	for(auto it:diag1) ans+=it.second*(it.second-1);
	for(auto it:diag2) ans+=it.second*(it.second-1);
	cout<>t;
	while(t--) solve();
	return 0;
}