【树】二叉树顺序结构

二叉树顺序存储方式，定义了数据域，左结点，右结点，和父节点

#define MAXLen 100
typedef char Data;

typedef struct ChainTree{
	Data NodeData;  //元素数据
	struct ChainTree *LsonNode; //左子树结点指针
	struct ChainTree *RsonNode; //右子树结点指针
	struct ChainTree *PerentNode; //父结点指针
}ChainTreeType;

ChainTreeType *root=NULL;

根据上面的数据结构的方式，我们来定义个完整的二叉树：
第一步：定义一个数据结构

#define MAXLen 20   //最大长度
typedef char Data;   //定义元素类型

typedef struct CBT{  //定义二叉树结点类型
	Data data;
	struct CBT *left;
	struct CBT *right;
}CBTType;

第二步：初始化二叉树,
在使用顺序表之前，首先要初始化二叉树，代码中只需要将一个结点设置为二叉树的根结点。那么我们需要首先申请内存，然后由确定一个根结点数据，并将指向左子树和右子树的指针设置为空，就完成了二叉树的初始化工作。

CBTType *InitTree(){
	CBTType *node;
	if(node=(CBTType*)malloc(sizeof(CBTType))) //申请内存空间
	{
		print("please enter data of root node:\n");
		scanf("%s",&node->data); //输入根节点数据
		node->left=NULL; // 左结点和右结点都设置为空
		node->right=NULL;
		if(node!=NULL){
			return node;
		}
		else{
			return NULL;
		}
	}
	return NULL;
}

第三步：添加数据,
添加结点就是在二叉树中添加结点数据。添加结点时除了要输入结点数据外，还需要指定其父结点，以及添加的结点时作为左子树还是作为右子树。我们输入参数treeNode为二叉树的根结点，传入根结点方便在代码中进行查找。代码中首先申请内存，然后由用户输入二叉树结点数据，并设置左右子树为空。接着指定其父结点，最后设置其作为左子树还是作为右子树。

void AddTreeNode(CBTType *treeNode) //添加结点
{
	CBTType *pnode, *parent;
	DATA data;
	char menusel; //定义操作符
	if(pnode=(CBTTYPE*)malloc(sizeof(CBTType)))//分配内存 
	{
		printf("please enter CBTTree data:\n");
		fflush(stdin);//stdin:标准输入流，fflush（stdin）清空输入缓存区。
		//fflush(stdout) 强制显示输出缓冲区，rewind(stdin) 也可以清空输入缓存区，可以屏蔽回车符号。
		scanf("%s",&pnode->data);
		pnode->left=NULL; //设置左右树为空
		pnode->right=NULL;
		
		printf("please enter parent data of CBTTree");
		fflush(stdin);
		scanf("%s", &data);
		parent=TreeFindNode(treeNode.data);//查找指定数的结点
		if(!parent){                       //如果没有找到
			printf("does not found parent node!");
			free(pnode);                   //释放创建的结点内存
			return;
		} 
		printf("1.add this node to left tree\n2.add this node to right tree\n");
		do
		{
			menusel=getch();               //输入选择项，操作符
			menusel-='0';
			if(menusel==1 || menusel==2)
			{
				if(parent==NULL){
					printf("the parent node does not exist, please set parent node first!";)
				}
				else{
					switch(menusel)
					{
						case 1:               //添加到左结点
							if(parent->left){  //左子树不为空
								printf("left node can't empty!");
							}
							else{
								parent->left = pnode;
							}
							break;
						case 2:                 //添加到右结点
							if(parent->right){  // 右结点不为空
								printf("Right node can't empty!'"); 
							}
							else{
								parent->right = pnode;
							}
							break;
						default:
							printf("invalid input!\n");
					}
				}
				
			}	
		}while(menusel!=1 && menusel!=2);
	} 
}

第四步：查找结点
查找结点就是遍历二叉树中的每一个结点，逐个比较数据，当找到目标数据时将返回该数据所在结点的指针。我们这里输入参数treeNode为待查找的二叉树的根结点，输入参数data为待查找的结点数据，代码中首先判断根结点是否为空，然后分别向左右子树递归查找。如果当前结点的数据与查找数据相等，则返回当前结点的指针。

CBTType *TreeFineNode(CNBType *treeNode, DATA data){
	CBTType *ptr;
	if(treeNode == NULL){
		return NULL;
	}
	else{
		if(treeNode->data==data){
			return treeNode;
		}
		else{                         //分别向左右子树递归查找。
			if(ptr==TreeFindNode(treeNode->left,data)){
				return ptr;
			}
			else if(ptr==TreeFindNode(treeNode->right,data)){
				return ptr;
			}
			else{
				return NULL;
			}
		}
	}
}

第5步：获取左子树/右子树
获取左子树就是返回当前结点的左子树结点的值，由于我们在二叉树结构中定义了相应的指针，
所以操作就比较简单了。其中参数treeNode为二叉树的一个结点。代码将返回该结点的左子树的指针。 右子树和左子树的做法相同。

CBTType *TreeleftNode(CBTType *treeNode)
{
	if(treeNode)
	{
		return treeNode->left; //返回值
	}
	else
	{
		return NULL;
	}
}

CBTType *TreerightNode(CBTType *treeNode)
{
	if(treeNode){
		return treeNode->right;
	}
	else
	{
		return NULL;
	}
}

第6步：判断空树
判断空树就是判断一个二叉树结构是否为空。如果是空树，则表示该二叉树结果中没有数据。
参数treeNode为待判断的二叉树的根结点。该函数检查二叉树是否为空，为空则返回1，否则返回0.

int TreeIsEmpty(CBTType *treeNode)
{
	if(treeNode){
		return 0;
	}
	else
	{
		return 1;
	}
}

第7步：计算二叉树的深度。
计算二叉树的深度就是计算二叉树中结点的最大层数，这里往往需要采用递归算法来实现, 另外还可以使用迭代的方法来实现。
递归方法：

1. 如果根节点为空，返回0。
2. 否则，递归计算左子树和右子树的深度。
3. 返回左右子树深度的较大值+1，即为整个树的深度。

int TreeDepth(CBTType *treeNode)
{
	int depleft,depright;
	if(treeNode==NULL)
	{
		return 0;   //对于空树，深度为0；
	}
	else
	{
		depleft=TreeDepth(treeNode->left); //左子树深度（递归调用）
		deprgiht=TreeDepth(treeNode->right); //右子树深度（递归调用）
		//return max(depleft, deprgiht) + 1;
		if(depleft>deprifht)
		{
			return depleft+1;
		}
		else{
			return depright+1;
		}
	}
}

迭代方法：

使用一个队列存储每一层的节点。
首先将根节点入队。
当队列不为空时，取出队列中所有的节点，并将它们的非空子节点入队。
每一轮结束后，深度+1。
1
/ \
2 3
/ \ /
4 5 6 7

首先将根节点(1, 1)压入栈中，其中1表示深度为1。

接着弹出栈顶节点(1, 1)，并将其子节点(2, 2)和(3, 2)分别压入栈中。

再弹出栈顶节点(3, 2)，不需要将其子节点压入栈中。

接着弹出栈顶节点(2, 2)，并将其子节点(4, 3)和(5, 3)分别压入栈中。

再依次弹出栈顶节点(5, 3)、(4, 3)，不需要将其子节点压入栈中。

最后栈为空，返回最大深度3。

int maxDepth(TreeNode* root) {    
	if(!root) return 0;    
	stack<pair<TreeNode*, int>> s; // pair中存放节点和深度    
	s.push(make_pair(root, 1));    
	int depth = 0;    
	while(!s.empty()) {        
		auto cur = s.top();        
		s.pop();        
		depth = max(depth, cur.second);        
		if(cur.first->right) s.push(make_pair(cur.first->right, cur.second+1));        
		if(cur.first->left) s.push(make_pair(cur.first->left, cur.second+1));    
	}    
	return depth;
}

make_pair 是 C++ STL 中的一个函数模板，用于创建一个 pair 对象，即将两个值（可以是不同类型）打包成一对。它的声明如下：

template<class T1, class T2>
constexpr pair<V1,V2> make_pair(T1&& t, T2&& u);

其中，T1 和 T2 可以是任意类型，t 和 u 是对应类型的参数，可以是左值或右值引用。make_pair 函数会根据 t 和 u 的类型自动推导出 pair 的类型，返回一个值为 pair 类型的对象。

constexpr是C++11引入的关键字，用于指示编译器在编译期间计算表达式的值，并将其用于编译时计算。它可以应用于函数、变量或者类的成员函数和静态成员变量，以及常量表达式。
当一个函数或变量被声明为constexpr时，它的值必须可以在编译期间计算，这意味着它不能有任何运行时的副作用，例如读取文件或从网络获取数据。其主要应用包括：
常量表达式：使用constexpr将变量或函数声明为常量表达式，可以在编译期间进行计算，并且被用作常量。
性能优化：使用constexpr可以告诉编译器在编译期间计算表达式，从而在运行时节省时间和资源。

例如，可以这样使用 make_pair 函数：

#include 
#include 
using namespace std;
int main() {    
	int a = 10;    
	double b = 3.14;    
	auto p = make_pair(a, b);    
	cout << p.first << " " << p.second << endl;  
	// 输出：10 3.14    
	return 0;
}

这段代码中，我们用 make_pair 函数将一个 int 类型的变量 a 和一个 double 类型的变量 b 打包成了一个 pair 对象 p，并输出了其中的两个值。

第八步：清空二叉树
清空二叉树就是将二叉树变成一个空树，这里也需要使用递归算法来实现。

void clearTree(CBTType *treeNode){
	if(treeNode)
	{
		clearTree(treeNode->left); //清空左子树
		clearTree(treeNode->right); //清空右子树
		free(treeNode);             //释放当前结点所占内存
		treeNode=NULL;
	}
}

第九步：显示结点数据。
显示结点数据就是显示当前结点的数据内容。
其中参数p为待显示的结点。

void TreeNodeData(CBTType *p)
{
	printf("%c", p->data);
}

遍历二叉树
遍历二叉树就是逐个查找二叉树中所有的结点，这是二叉树的基本操作，因为很多操作都需要首先遍历整个二叉树，由于二叉树的特殊结构，我们有多种方法来进行遍历。
按层遍历算法是最直观的遍历算法。首先处理第1层即根结点，再处理第1根结点的左右子树，
也即是第2层…就这样循环处理，就可以逐层遍历。
参数treeNode为需要遍历的二叉树根结点，而函数指针p是一个需要对结点进行操作的函数。
在整个代码处理过程中，首先从根结点开始，将每层的结点逐步进入队列，这样就可得到按层
遍历的效果。

二叉树按层遍历的过程，也叫做广度优先遍历，可以使用队列来实现。

具体步骤如下：

1. 首先将根节点入队。

2. 当队列不为空时，依次进行如下操作：

   弹出队首元素，并输出该元素的值。

   如果该元素有左子树，则将左子树入队。

   如果该元素有右子树，则将右子树入队。

3. 遍历完成后，队列中没有元素，算法结束。

假设有如下一棵二叉树：
1
/ \
2 3
/ \
4 5 6

按层遍历的过程为：
先访问根节点1，
然后按照从上到下、从左到右的顺序依次访问其左右子节点2、3，
再按照同样的方式依次访问2的左右子节点4、5、3的右子节点6。
因此，按层遍历的结果为：1, 2, 3, 4, 5, 6。

void LevelFree(CBTType *treeNode, void(*TreeNodeData)(CBTType *p)) //按层遍历
{
	CBTType *p;
	CBTType *q[MAXLEN];    //定义一个顺序栈
	int head=0, tail=0;
	
	if(treeNode)      //如果队首指针不为空
	{
		tail=(tail+1)%MAXLEN;  //计算循环队列队尾序号
		q[tail]=treeNode;    //将二叉树根指针进队
	}
	while(head!=tail)          //队列不为空，进行循环
	{
		head=(head+1)%MAXLEN;   //计算循环队列的队首序号
		p=q[head];              //获取队首元素
		TreeNodeData(p);        //处理队首元素
		if(p->left!=NULL)       //如果结点存在左子树
		{
			tail=(tail+1)%MAXLEN;  //计算循环队列的队尾序号
			q[tail]=p->left;       //将左子树指针进队
		}
		if(p->right!=NULL)          //如果结点存在右子树
		{
			tail=(tail+1)%MAXLEN;   //计算循环队列的队尾序号
			q[tail]=p->right;       //将右子树指针进队
		}
	}
}

我们也可以使用队列来实现：

#include 
#include 
using namespace std;
struct TreeNode {    
	int val;    
	TreeNode* left;    
	TreeNode* right;    
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
void levelOrder(TreeNode* root) {    
	if (root == NULL) {        
		return;    
	}    
	queue<TreeNode*> q;    
	q.push(root);    
	while (!q.empty()) {        
		TreeNode* cur = q.front();        
		q.pop();        
		cout << cur->val << " ";        
		if (cur->left) {            
			q.push(cur->left);        
			}        
		if (cur->right) {            
			q.push(cur->right);        
			}    
	}
}
int main() {    
	TreeNode* root = new TreeNode(1);    
	root->left = new TreeNode(2);    
	root->right = new TreeNode(3);    
	root->left->left = new TreeNode(4);    
	root->left->right = new TreeNode(5);    
	root->right->left = new TreeNode(6);    
	root->right->right = new TreeNode(7);    
	cout << "按层遍历结果：";    
	levelOrder(root);    
	return 0;
}

先序遍历算法
先序遍历算法就是先按中序遍历左子树，再访问根结点，最后按中序遍历右子树。
程序可以按照递归的思路来遍历整个二叉树。
参数treeNode为需要遍历的二叉树根结点，函数指针p是一个需要对结点进行操作的函数。

void DLRTree(CBTType *treeNode,void(*TreeNodeData)(CBTType *p)) //先序遍历
{
	if(treeNode)
	{
		TreeNodeData(treeNode);  //显示结点的数据
		DLRTree(treeNode->left,TreeNodeData);
		DLRTree(treeNode->right,TreeNodeData); 
	}
}

中序遍历算法
中序遍历就是先访问根结点，在按先序遍历左子树，最后按先序遍历右子树。

void LDRTree(CBTType *treeNode,void(*TreeNodeData)(CBTType *p)) //中序遍历
{
	if(treeNode)
	{
		LDRTree(treeNode->left,TreeNodeData);  //中序遍历左子树
		TreeNodeData(treeNode);                //显示结点数据
		LDRTree(treeNode->right,TreeNodeData);  //中序遍历右子树
	}
}

后序遍历算法：
后序遍历算法就是先按后序遍历左子树，再按后序遍历右子树，最后访问根结点。

void LRDTree(CBTType *treeNode,void(*TreeNodeData)(CBTType *p)) //后序遍历
{
	if(treeNode)
	{
		LRDTree(treeNode->left, TreeNodeData);  //后序遍历左子树
		LRDTree(treeNode->right,TreeNodeData);  //后序遍历右子树
		TreeNodeData(treeNode);                 //显示结点数据
	}
}

二叉树操作实例

#include
#include
#include
#include
#include
#define MAXTSIZE 1000
using namespace std;

typedef struct BiTNode
{
    char data; // 结点数据域 
    struct BiTNode *lchild,*rchild; // 左右孩子指针 
}BiTNode,*BiTree;


void CreateBiTree(BiTree &T) // 先序遍历建立二叉链表 
{
    char ch;
    cin>>ch;
    if(ch=='#')
        T=NULL;
    else
    {
        T=(BiTNode *)malloc(sizeof(BiTNode));
        T->data=ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
}

void travel1(BiTree T) // 先序遍历 
{
    if(T)
    {
        printf("%c",T->data);
        travel1(T->lchild);
        travel1(T->rchild);
    }
}

void travel2(BiTree T) // 中序遍历 
{
    if(T)
    {
        travel2(T->lchild);    
        printf("%c",T->data);
        travel2(T->rchild);
    }
}

void travel3(BiTree T) // 后序遍历 
{
    if(T)
    {
        travel3(T->lchild);
        travel3(T->rchild);
        printf("%c",T->data);
    }
}

int NodeCount(BiTree T)//统计二叉树中结点的个数
     {
     if(T==NULL)  return 0; //如果是空树，则结点个数为0, 递归结束
	 else return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
	 } 
	  
int count(BiTree T) // 计算叶子结点的个数 
{
    if(T==NULL)  return 0;
    int cnt=0;
    if((!T->lchild)&&(!T->rchild))
    {
        cnt++;
    }
    int leftcnt=count(T->lchild);
    int rightcnt=count(T->rchild);
    cnt+=leftcnt+rightcnt;
    return cnt;
}

int Depth(BiTree T) // 计算二叉树的深度 
{
    if(T==NULL)    return 0;
    else
    {
        int m=Depth(T->lchild);
        int n=Depth(T->rchild);
        return m>n?(m+1):(n+1);
    }
}

void exchange(BiTree T,BiTree &NewT) // 交换左右子树 
{
    if(T==NULL)
    {
        NewT=NULL;
        return ;
    }
    else
    {
        NewT=(BiTNode *)malloc(sizeof(BiTNode));
        NewT->data=T->data;
        exchange(T->lchild,NewT->rchild); // 复制原树的左子树给新树的右子树 
        exchange(T->rchild,NewT->lchild); // 复制原树的右子树给新树的左子树 
    }
}
int NodeNumber_1(BiTree T)  //统计二叉树的度为1的结点个数； 
{
	int i=0;
	if(T)
	{
		if( (T->lchild==NULL&&T->rchild!=NULL) ||(T->lchild!=NULL&&T->rchild==NULL))
		{
			i=1+NodeNumber_1(T->lchild)+NodeNumber_1(T->rchild);
		}
		else
		{
			i=NodeNumber_1(T->lchild)+NodeNumber_1(T->rchild);
		} 
	}
	return i;
}
int main()
{
    puts("**************************");
    puts("1. 建立二叉树"); 
    puts("2. 先序遍历二叉树");
    puts("3. 中序遍历二叉树");
    puts("4. 后序遍历二叉树");
    puts("5. 计算结点个数"); 
    puts("6. 计算叶子结点个数"); 
    puts("7. 计算二叉树的深度"); 
    puts("8. 统计二叉树的度为1的结点个数；");
    puts("9. 交换二叉树的左右子树");  
    puts("0. 退出");
    puts("**************************");
    BiTree Tree,NewTree;
    int choose;
    while(~scanf("%d",&choose),choose)
    {
        switch(choose)
        {
            case 1:
                puts("以 '#' 为左/右子树空的标志!"); 
                CreateBiTree(Tree);
                break;
            case 2:
                printf("先序遍历结果为："); 
                travel1(Tree);
                puts("");
                break;
            case 3:
                printf("中序遍历结果为："); 
                travel2(Tree);
                puts("");
                break;
            case 4:
                printf("后序遍历结果为："); 
                travel3(Tree);
                puts("");
                break;
            case 5:
                printf("结点个数为：%d\n",NodeCount(Tree));
                break;
            case 6:
                printf("叶子结点个数为：%d\n",count(Tree));
                break;
            case 7:
                printf("二叉树的深度为：%d\n",Depth(Tree));
                break;
            case 8:
                printf("度为1的结点个数：%d\n",NodeNumber_1(Tree));
                break;
            case 9:
                exchange(Tree,NewTree);
                Tree=NewTree;
                puts("交换成功！\n"); 
                break;
        }
    }
    system("pause");
    return 0;
}

【基础题1】求二叉树的最大层数(最大深度)

递归法
1.确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
代码如下：

int getDepth(TreeNode* node)

2.确定终止条件：如果为空节点的话，就返回0，表示高度为0。
代码如下：

if (node == NULL) return 0;

3.确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
代码如下：

int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右
int depth = 1 + max(leftDepth, rightDepth); // 中
return depth;

#include 
using namespace std;
	
typedef struct CBT{
	char data;
	struct CBT *rightchild;
	struct CBT *leftchild;
}CBTType, *CBTTree;

void createCBTTree(CBTTree &Tree){
	char ch;
	cin>>ch;
	if(ch=='#') Tree=NULL;
	else{
		Tree=(CBTType *)malloc(sizeof(CBTType));
		Tree->data=ch;
		createCBTTree(Tree->rightchild);
		createCBTTree(Tree->leftchild);
	}
}

int GetDepth(CBTTree Tree){
	if(Tree==NULL) return 0;
	else{
		int leftDepth=GetDepth(Tree->rightchild);
		int rightDepth=GetDepth(Tree->leftchild);
		int depth = 1 + max(leftDepth, rightDepth); 
		return depth;
	}
}

int main(){
	CBTTree tree;
	createCBTTree(tree);
	printf("%d", GetDepth(tree));
}

输入：abc##de#g##f### （前序）
输出：5

【基础题2】二叉树的最小深度

#include 
using namespace std;
	
typedef struct CBT{
	char data;
	struct CBT *rightchild;
	struct CBT *leftchild;
}CBTType, *CBTTree;


void createCBTTree(CBTTree &Tree){
	char ch;
	cin>>ch;
	if(ch=='#') Tree=NULL;
	else{
		Tree=(CBTType *)malloc(sizeof(CBTType));
		Tree->data=ch;
		createCBTTree(Tree->rightchild);
		createCBTTree(Tree->leftchild);
	}
}

int SmallestDepth(CBTTree bt){
	if(bt==NULL)
		return 0;	
	if(bt->leftchild==NULL)
		return SmallestDepth(bt->rightchild)+1;
	if(bt->rightchild==NULL)
		return SmallestDepth(bt->leftchild)+1;	
	int m =	SmallestDepth(bt->leftchild)+1;
	int n =	SmallestDepth(bt->rightchild)+1;
	return m<n?m:n;
}

int main(){
	CBTTree tree;
	createCBTTree(tree);
	printf("%d",SmallestDepth(tree));
}

输入：A B # # C D # # #（前序）
输出：2

【基础题3】平衡树_Balanced Binary Tree (Easy)(AVL)

【基础题4】 两节点的最长路径

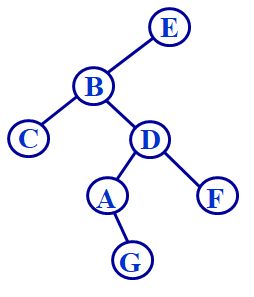
输入 EBC##DA#G##F###
输出：4
路径为：E->B->D->A->G->NULL

#include
#include 
#define MAX  200
typedef char TElemType;
typedef int status; 
typedef struct BiNode
{
	TElemType data;
	struct BiNode *lchild;
	struct BiNode *rchild;
}BiNode,*BiTree;
void CreateBiTree(BiTree &T)//二叉树的先序创建 
{
	TElemType ch;
	scanf("%c",&ch);
	if(ch=='#')
		T=NULL;
	else 
	{
		T=(BiNode*)malloc(sizeof(BiNode));
		if(!T)
			exit(-1);
		T->data=ch;
		CreateBiTree(T->lchild);
		CreateBiTree(T->rchild);
	}
}
void longest_path(BiTree T,int *path,int &len,int *longestpath,int &longest_len)
{
	if(T!=NULL)
	{
		if(T->lchild==NULL&&T->rchild==NULL)//当遇到叶子结点时，该条路径完毕 
		{
			path[len]=T->data;
			if(len>longest_len)//如果长于longest_len就替换 
			{
				for(int j=0;j<=len;j++)
				{
					longestpath[j]=path[j];
				}
				longest_len=len;//longest_len更新 
			}
		}
		else//当遇到的不是叶子结点时，该条路径继续 
		{
			path[len++]=T->data;
			longest_path(T->lchild ,path,len,longestpath,longest_len);
			longest_path(T->rchild ,path,len,longestpath,longest_len);
			len--;
		}
	}
}
int main()
{
	BiTree T;
	printf("创建树输入树T的先序序列(其中使用#代表空节点)\n");
	CreateBiTree(T);
	int path[MAX]={0};
	int longestpath[MAX]={0};
	int len=0;
	int longest_len=0;
	longest_path(T,path,len,longestpath,longest_len);
	printf("第一条最长的路径长度为：%d\n",longest_len);
	printf("路径为："); 
	for(int i=0;i<=longest_len;i++)
	{
		
		printf("%c ->",longestpath[i]);
	}
	printf("NULL");
	
}

【基础题5】翻转树

【基础题6】 归并两棵树

【基础题7】判断路径和是否等于一个数

【基础题8】 统计路径和等于一个数的路径数量

【基础题9】树的对称

【基础题10】求二叉树的镜像

【例题1】普通二叉树（简化版）

题目描述

您需要写一种数据结构，来维护一些数（ 都是 $10^9$ 以内的数字）的集合，最开始时集合是空的。其中需要提供以下操作，操作次数 $q$ 不超过 $10^4$：

1. 查询 $x$ 数的排名（排名定义为比当前数小的数的个数 $+1$。若有多个相同的数，应输出最小的排名）。
2. 查询排名为 $x$ 的数。
3. 求 $x$ 的前驱（前驱定义为小于 $x$，且最大的数）。若未找到则输出 $-2147483647$。
4. 求 $x$ 的后继（后继定义为大于 $x$，且最小的数）。若未找到则输出 $2147483647$。
5. 插入一个数 $x$。

输入格式

第一行是一个整数 $q$，表示操作次数。

接下来 $q$ 行，每行两个整数 $op,x$，分别表示操作序号以及操作的参数 $x$。

输出格式

输出有若干行。对于操作 $1,2,3,4$，输出一个整数，表示该操作的结果。

样例 #1

样例输入 #1

7
5 1
5 3
5 5
1 3
2 2
3 3
4 3

样例输出 #1

2
3
1
5

[例题2] 求先序排列

题目描述

给出一棵二叉树的中序与后序排列。求出它的先序排列。（约定树结点用不同的大写字母表示，且二叉树的节点个数 $ \le 8$）。

输入格式

共两行，均为大写字母组成的字符串，表示一棵二叉树的中序与后序排列。

输出格式

共一行一个字符串，表示一棵二叉树的先序。

样例 #1

样例输入 #1

BADC
BDCA

样例输出 #1

ABCD

提示

【题目来源】

NOIP 2001 普及组第三题

[例题3]二叉树问题

题目描述

如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

• 深度：$4$
• 宽度：$4$
• 结点 8 和 6 之间的距离：$8$
• 结点 7 和 6 之间的距离：$3$

其中宽度表示二叉树上同一层最多的结点个数，节点 $u,v$ 之间的距离表示从 $u$ 到 $v$ 的最短有向路径上向根节点的边数的两倍加上向叶节点的边数。

给定一颗以 1 号结点为根的二叉树，请求出其深度、宽度和两个指定节点 $x,y$ 之间的距离。

输入格式

第一行是一个整数，表示树的结点个数 $n$。
接下来 $n-1$ 行，每行两个整数 $u,v$，表示树上存在一条连接 $u,v$ 的边。
最后一行有两个整数 $x,y$，表示求 $x,y$ 之间的距离。

输出格式

输入三行，每行一个整数，依次表示二叉树的深度、宽度和 $x,y$ 之间的距离。

样例 #1

样例输入 #1

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

样例输出 #1

4
4
8

提示

对于全部的测试点，保证 $1\le u,v,x,y\le n\le 100$，且给出的是一棵树。

[例题4]医院设置

题目描述

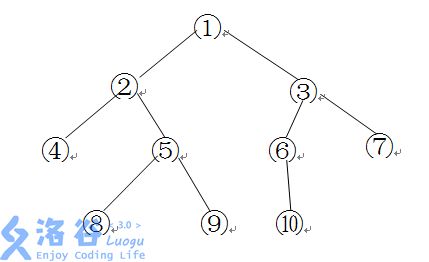
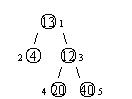
设有一棵二叉树，如图：

其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 $1$。如上图中，若医院建在1 处，则距离和 $=4+12+2\times 20+2\times 40=136$；若医院建在 $3$ 处，则距离和 $=4\times 2+13+20+40=81$。

输入格式

第一行一个整数 $n$，表示树的结点数。

接下来的 $n$ 行每行描述了一个结点的状况，包含三个整数 $w,u,v$，其中 $w$ 为居民人口数，$u$ 为左链接（为 $0$ 表示无链接），$v$ 为右链接（为 $0$ 表示无链接）。

输出格式

一个整数，表示最小距离和。

样例 #1

样例输入 #1

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

样例输出 #1

81

提示

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n\le 100$，$0\le u,v\le n$，$1\le w\le 10^5$。

【例题5】淘汰赛

题目描述

有 $2^n$（$n\le 7$）个国家参加世界杯决赛圈且进入淘汰赛环节。已经知道各个国家的能力值，且都不相等。能力值高的国家和能力值低的国家踢比赛时高者获胜。1 号国家和 2 号国家踢一场比赛，胜者晋级。3 号国家和 4 号国家也踢一场，胜者晋级……晋级后的国家用相同的方法继续完成赛程，直到决出冠军。给出各个国家的能力值，请问亚军是哪个国家？

输入格式

第一行一个整数 $n$，表示一共 $2^n$ 个国家参赛。

第二行 $2^n$ 个整数，第 $i$ 个整数表示编号为 $i$ 的国家的能力值（$1\le i\le 2^n$）。

数据保证不存在平局。

输出格式

仅一个整数，表示亚军国家的编号。

样例 #1

样例输入 #1

3
4 2 3 1 10 5 9 7

样例输出 #1

1