利用遗传算法解决旅行商问题（GA-TSP）—— Python代码实现

旅行商问题

旅行商问题是指一个旅行商从某个城市出发，依次到达所有城市，使得总路程最短

遗传算法

编码方案

在旅行商问题中，编码方案采取整数编码，即染色体上的每个基因均表示城市的编号，染色体即表示一种旅行商路径。

上述例子中，即表示一种旅行商的路径为7->1->0->4->5->6->3->2

适应度

适应度即表示一个个体对环境的适应能力，适应能力越好的个体应当被保留下来进行繁衍，故适应度越高，对环境的适应能力越高，在每次选择时，应当选择适应度较高的个体进行保留。

在旅行商问题中，每个个体的适应度为路径的总成本大小：
$$fitness=distence(route)$$
以上述个体$7-1-0-4-5-6$为例，该个体的适应度即为$$fitness=dis(7->1)+dis(1->0)+dis(0->4)+dis(4->5)+dis(4->5)+dis(5->6)+dis(6->3)+dis(3->2)+dis(2->7)$$

即为整条路径的总距离长度

交叉算子

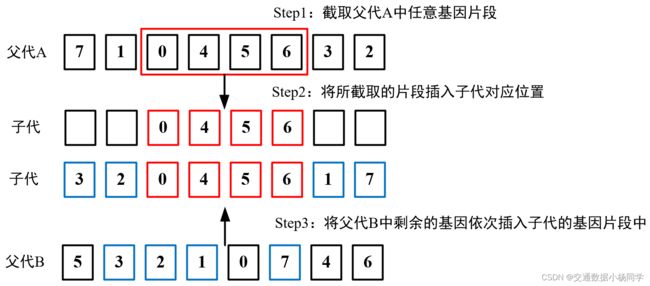
顺序交叉

此处采用顺序交叉（Order Crossover, OX）。顺序交叉是一种遗传算法中常用的交叉方法，它用于解决排列问题。在这种交叉方法中，首先从一个父代基因组中随机截取一段基因片段，并将其复制到子代基因组的对应位置上。然后，从另一个父代基因组中选择剩余的基因，按照其在父代基因组中出现的顺序填充到子代基因组中的空位上。这样可以保证子代基因组中基因的顺序与父代基因组相同。

个体选择

轮盘赌选择

轮盘赌选择法（roulette wheel selection）是一种最简单也是最常用的选择方法。在该方法中，各个个体的选择概率和其适应度值成比例，适应度越大，选中概率也越大。轮盘赌选择法的过程如下：

1. 计算每个个体的被选中概率$p(x_i)$。
2. 计算每个部分的累积概率$q(x_i)$。
3. 随机生成一个数组$m$，数组中的元素取值范围在0和1之间，并将其按从小到大的方式进行排序。
4. 若累积概率$q(x_i)$大于数组中的元素$m[i]$，则个体$x(i)$被选中，若小于$m[i]$，则比较下一个个体$x(i+1)$直至选出一个个体为止。
5. 若需要转中$N$个个体，则将步骤3重复$N$次即可

锦标赛选择

锦标赛选择法的基本思想是每次从种群中随机取出一定数量的个体，然后选择其中最好的一个进入子代种群。重复该操作，直到新的种群规模达到原来的种群规模。具体的操作步骤如下：

1. 确定每次选择的个体数量$N$（二元锦标赛选择即选择2个个体）。
2. 从种群中随机选择$N$个个体（每个个体被选择的概率相同），根据每个个体的适应度值，选择其中适应度值最好的个体进入下一代种群。
3. 重复步骤2多次（重复次数为种群的大小），直到新的种群规模达到原来的种群规模

精英选择法

精英选择法的基本思想是：在每一代中，将种群中适应度最高的若干个体直接复制到下一代种群中，以保留当前种群中的优秀基因。精英选择法可以防止遗传算法在进化过程中出现“早熟”现象，即算法过早地收敛到局部最优解而无法继续搜索全局最优解。精英选择法的步骤如下：

1. 在每一代中，计算种群中每个个体的适应度值。
2. 从种群中选择适应度值最高的若干个体。
3. 将这些个体直接复制到下一代种群中。
4. 使用其他选择方法（如轮盘赌选择、锦标赛选择等）从剩余个体中选择其他个体进入下一代种群，直到新的种群规模达到原来的种群规模。

变异算子

逆序交叉

此处采用逆序交叉，首先从个体中随机选择两个位置，然后将这两个位置之间的元素（包括这两个位置）逆序。最后返回变异后的个体。

利用Python编写的GA-TSP算法

class TSP_GA:
    def __init__(self,
                 iteration,
                 cost_mat,
                 pop_size,
                 mutation_rate,
                 elite_rate,
                 cross_rate):
        self.iteration = iteration # 迭代次数
        self.cost_mat = cost_mat # 成本矩阵
        self.cities = self.cost_mat.shape[0]  # 城市个数
        self.pop_size = pop_size # 种群数量
        self.mutate_rate = mutation_rate # 变异率
        self.elite_rate = elite_rate # 精英率

    def initial_population(self): # 种群初始化
        population = []
        for i in range(self.pop_size):
            cities_list = list(range(self.cities))
            random.shuffle(cities_list)
            population.append(cities_list)
        return population

    def fitness(self, individual): # 计算每个个体的适应度
        route_cost = 0
        for i in range(len(individual) - 1):
            start = individual[i]
            end = individual[i + 1]
            route_cost += self.cost_mat[start][end]
        route_cost += self.cost_mat[individual[-1]][individual[0]]
        return route_cost

    @staticmethod
    def __crossover(parent_a, parent_b): # 交叉
        """
        :param parent_a: 父代基因A
        :param parent_b: 父代基因B
        :return:
        """
        child = [None] * len(parent_a)  # 创建一个子代个体
        start_index, end_index = random.sample(range(len(parent_a)), 2)  # 随机生成两个索引点，用于截取基因片段
        if start_index > end_index:
            start_index, end_index = end_index, start_index
        child[start_index:end_index] = parent_a[start_index:end_index]  # 截取父代基因A中的片段，并赋给子代基因的对应位置
        remaining_genes = [gene for gene in parent_b if gene not in child]  # 从另一个父代基因组中选择剩余的基因
        i = 0
        for gene in remaining_genes:
            while child[i] is not None:  # 找到子代基因组中的空位
                i += 1
            child[i] = gene  # 将基因填充到子代基因组中
        return child  # 返回子代基因组

    def select_elites(self, population, fitnesses): # 精英选择
        # 计算被选出精英个体的数量
        num_elites = int(len(population) * self.elite_rate)  # 精英数量

        # 根据适应度对种群进行排序
        sorted_population = [individual for _, individual in sorted(zip(fitnesses, population))]

        # 选取适应度大的前几个
        elites = sorted_population[:num_elites]

        return elites

    def select_two_parents(self, population, fitnesses): #
        total_fitness = sum(fitnesses)
        selection_probability = [fitness / total_fitness for fitness in fitnesses]

        # 选择父代 A
        parent_a_index = random.choices(range(len(population)), weights=selection_probability, k=1)[0]
        parent_a = population[parent_a_index]

        # 选择父代 B
        population_without_a = population[:parent_a_index] + population[parent_a_index + 1:]
        fitnesses_without_a = fitnesses[:parent_a_index] + fitnesses[parent_a_index + 1:]
        total_fitness = sum(fitnesses_without_a)
        selection_probability = [fitness / total_fitness for fitness in fitnesses_without_a]
        parent_b_index = random.choices(range(len(population_without_a)), weights=selection_probability, k=1)[0]
        parent_b = population_without_a[parent_b_index]

        return parent_a, parent_b


    def displacement_mutation(self, individual):
        """
        置换变异
        :param individual: 个体
        """
        i, j = sorted(random.sample(range(len(individual)), 2))
        k = random.randint(0, len(individual) - (j - i + 1))
        genes = individual[i:j + 1]
        del individual[i:j + 1]
        individual[k:k] = genes
        return individual



    def solve(self):
        population = self.initial_population()  # init polpulation
        best_fitness = []
        for i in range(self.iteration):  # iteration
            fitnesses = [self.fitness(individual) for individual in population]  # 求解每个个体的适应度并保存为列表
            next_population = self.select_elites(population, fitnesses)  # 精英选择
            while len(next_population) < self.pop_size:
                parent_a, parent_b = self.select_two_parents(population, fitnesses)
                child_a = self.__crossover(parent_a, parent_b)  # 交叉，生成子代个体a
                child_b = self.__crossover(parent_b, parent_a)  # 交叉，生成子代个体b
                if random.random() < self.mutate_rate:
                    child_a = self.displacement_mutation(child_a)  # 变异
                if random.random() < self.mutate_rate:
                    child_b = self.displacement_mutation(child_b)  # 变异
                next_population.append(child_a)  # 将子代基因组添加到新的种群中
                next_population.append(child_b)
            population = next_population
            fitnesses = [self.fitness(individual) for individual in population]  # 求解每个个体的适应度并保存为列表
            best_fitness.append(min(fitnesses))
            print('当前迭代进度:{}/{},最佳适应度为:{}'.format(i, self.iteration, min(fitnesses)))
        fitnesses = [self.fitness(individual) for individual in population]
        best_individual = population[fitnesses.index(min(fitnesses))]
        return best_individual, min(fitnesses), best_fitness

调用函数

TSP= TSP_GA(teration = 10000,
            cost_mat = distence_matrix,
            pop_size = 150,
            mutation_rate = 0.05,
            elite_rate = 0.4,
            cross_rate = 0.7) # 实例化，初始化参数
            
TSP_RESULT = TSP.solve() # 调用TSP_GA中的 solve求解函数

测试数据

ID	X	Y
1	1150	1760
2	630	1660
3	40	2090
4	750	1100
5	750	2030
6	1030	2070
7	1650	650
8	1490	1630
9	790	2260
10	710	1310
11	840	550
12	1170	2300
13	970	1340
14	510	700
15	750	900
16	1280	1200
17	230	590
18	460	860
19	1040	950
20	590	1390
21	830	1770
22	490	500
23	1840	1240
24	1260	1500
25	1280	790
26	490	2130
27	1460	1420
28	1260	1910
29	360	1980
centered	centered	centered

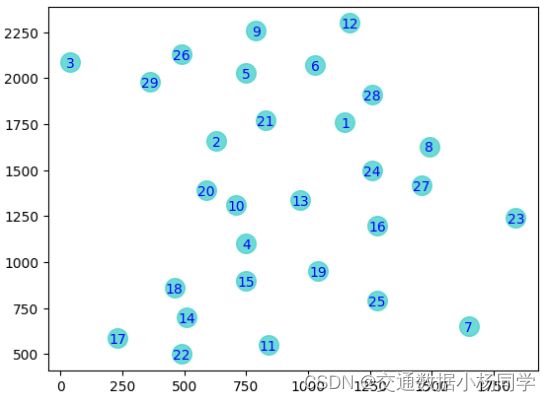
共有29个城市，依次编号为1-29

可视化

data = pd.read_csv('data.csv', header=None) # 测试数据集
data_dic = list(data.itertuples(index=False, name=None))
distances = squareform(pdist(data_dic)) # 生成距离矩阵
for point in data_dic:
    label, x, y = point
    plt.scatter(x, y,c='darkturquoise',s=220)
    plt.text(x, y, label, ha='center', va='center_baseline',fontdict={'size': 10, 'color': 'black'})

共有29个城市，依次编号为1-29

算法求解结果

此处由于城市数量过多，所以收敛的可能比较慢，在使用过程中需要根据实际需要调整变异概率、交叉概率以及不同算子，使得每次迭代所得到的种群多样性更丰富，进而使得算法尽快的收敛。