数据结构:迷宫问题(深度优先搜索)

先说一下开辟二维数组和一维数组的问题

假如说我要开辟一个一维数组,像DevC++是支持这样写代码的

#include
using namespace std;
int main()
{
	int n;
	cin>>n;
	int a[n];
	return 0;
 } 

我们可以输入一个变量n来开辟多大内存的数组

但是visual stdio编译器是不支持用变量来开辟数组的,那我们就需要去申请内存,就需要用到了malloc函数,头文件是

在visual stdio来申请一维数组,我们用malloc来申请想要大小的内存,假如说我想要存放int类型的数组,我们申请了之后用指针去指向这个内存,所以我们用int*来接收

#include
#include
using namespace std;
int main()
{
	int n;
	cin >> n;
	int* a = (int*)malloc(sizeof(int) * n);
	return 0;
}

在visual stdio来申请二维数组的过程,如图

我先去开辟一个一片空间去存放指针的地址,里面的指针存放的是一个数组,这样就可以来动态申请一个二维数组的了,要注意的是接收这片空间要用二级指针(里面存放的是一级指针)

#include 
#include
using namespace std;
int main()
{
	int n, m;
	cin >> n, m;
	int** a = (int**)malloc(sizeof(int*) * n);//二级指针,存放一级指针数组的地址
	for (int i = 0; i < n; i++)
	{
		a[i] = (int*)malloc(sizeof(int) * m);//将数组中的地址指向一个一维数组
	}
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			cin >> a[i][j];//一个一个的输入数组元素的值
		}
	}
	for (int i = 0; i < n; i++)
	{
		free(a[i]);//先释放掉一维数组的空间
	}
	free(a);//再释放一级指针数组
	a = NULL;
	return 0;
}

为了保证我们创建二维数组成功我们可以先写一个打印函数

void Print(int** a, int n, int m)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			cout<< a[i][j]<<" ";//一个一个的输入数组元素的值
		}
		cout << endl;
	}
}

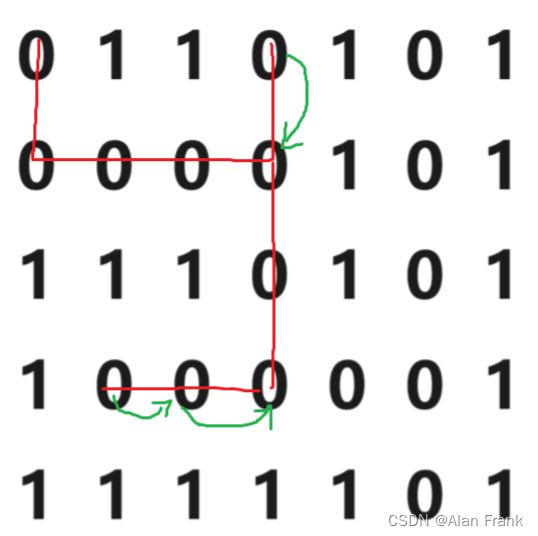
我们开始走迷宫,其实就是一个深度优化搜索的思想,就和之前的二叉树一样,我们先找完左树之后回溯到父节点,如果有右孩子就会走右孩子的节点,这个迷宫也一样,先按照一条路先走,如果这条路到最后走不通,那就回溯到上一个岔口处,走另一条路,知道找到出口或者都走完了找不到为止,我们画一个图

正确道路应该是上述这样的

但是我们编程的时候就让它去按照上下左右去找路,如果上能走那就一直走上,不能走再走下,如果下也不能走,就走左右,如果都不能走就回到上一个岔路口

注意我们设置的是上下左右,能走上先走上

就像这样上不能走了,就回到上一个岔路口,接着就该走下了

走着走着我们发现下面被墙挡住了,那我们就该走左了

左路不同就回到上一个岔路口处,接着就该往右走了

最后这样就算走出迷宫了

这就是我们说的深度优先搜索(一直往下找,找不到就换路,走别的路,还是沿着这条路往下走),一般这种dfs(深度优先搜索)用递归来解决

typedef struct Postion
{
	int row;
	int col;
}PT;
bool IsPath(int** a, int n, int m, PT pos)
{
	if (pos.row >= 0 && pos.row < n && pos.col >= 0 
		&& pos.col < m && a[pos.row][ pos.col] == 0)
	{
		return true;
	}
	else {
		return false;
	}
}
bool GetPath(int** a, int n, int m, PT cur)
{
	if (cur.row == n - 1 && cur.col == m - 1)
	{
		return true;
	}
	//探测cur位置的上下左右四个方向
	PT next = cur;
	a[cur.row][ cur.col] = 2;//避免走回头路
	//上
	next = cur;
	
	next.row -= 1;
	if (IsPath(a, n, m, next))
	{
		GetPath(a, n, m, next);
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPath(a, n, m, next))
	{
		GetPath(a, n, m, next);
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPath(a, n, m, next))
	{
		GetPath(a, n, m, next);
	}
	//右
	next = cur;
	next.col += 1;
	if (IsPath(a, n, m, next))
	{
		GetPath(a, n, m, next);
	}
}

我们先去定义一个结构体去存我们走的坐标,行和列都是从0开始的,然后我们定义了一个函数GetPath用了递归的方法,IsPath判断这条路能不能走通是用来,能走通就返回true我们就接着递归沿着这条路走,不能就换下一个方向

下一个重要的问题是我们需要打印坐标,我们就需要一个栈,因为我要走的坐标先出栈,如果不能通就出栈

stacks1;
bool GetPath(int** a, int n, int m, PT cur)
{
	s1.push(cur);
	if (cur.row == n - 1 && cur.col == m - 1)
	{
		return true;
	}
	//探测cur位置的上下左右四个方向
	PT next = cur;
	a[cur.row][ cur.col] = 2;//避免走回头路
	//上
	next = cur;
	
	next.row -= 1;
	if (IsPath(a, n, m, next))
	{
		GetPath(a, n, m, next);
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPath(a, n, m, next))
	{
		GetPath(a, n, m, next);
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPath(a, n, m, next))
	{
		GetPath(a, n, m, next);
	}
	//右
	next = cur;
	next.col += 1;
	if (IsPath(a, n, m, next))
	{
		GetPath(a, n, m, next);
	}
	s1.pop();
	return false;
}

我们先定义一个s1的栈,不管能不能走通我们先给他进栈,如果几个方向都不能走,就在false之前给他出栈,最后栈中剩下的就是能走到出口的坐标,但是这时候如果我们要打印栈,是反方向的,我们需要一个栈去把我们存放反方向坐标的栈给他倒过来

我们就这样来做

stacks2;
		int num = s1.size();
		for (int i = 0; i 

下面是完整代码

#include
#include
#include
#include
#include 
#include
#include
using namespace std;
typedef struct Postion
{
	int row;
	int col;
}PT;


bool IsPath(int** a, int n, int m, PT pos)
{
	if (pos.row >= 0 && pos.row < n && pos.col >= 0 
		&& pos.col < m && a[pos.row][ pos.col] == 0)
	{
		return true;
	}
	else {
		return false;
	}
}
stacks1;
bool GetPath(int** a, int n, int m, PT cur)
{
	s1.push(cur);
	if (cur.row == n - 1 && cur.col == m - 1)
	{
		return true;
	}
	//探测cur位置的上下左右四个方向
	PT next = cur;
	a[cur.row][ cur.col] = 2;//避免走回头路
	//上
	next = cur;
	
	next.row -= 1;
	if (IsPath(a, n, m, next))
	{
		if (GetPath(a, n, m, next))
		{
			return true;
		}
	}

	//下
	next = cur;
	next.row += 1;
	if (IsPath(a, n, m, next))
	{
		if (GetPath(a, n, m, next))
		{
			return true;
		}
	}

	//左
	next = cur;
	next.col -= 1;
	if (IsPath(a, n, m, next))
	{
		if (GetPath(a, n, m, next))
		{
			return true;
		}
	}
	//右
	next = cur;
	next.col += 1;
	if (IsPath(a, n, m, next))
	{
		if (GetPath(a, n, m, next))
		{
			return true;
	  	}
	}
	s1.pop();
	return false;
}
void Print(int** a, int n, int m)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			cout << a[i][j] << " ";//一个一个的输入数组元素的值
		}
		cout << endl;
	}
}
int main()
{
	int n = 0, m= 0;
	cin >> n>>m;
	cin.ignore();
	int** a = (int**)malloc(sizeof(int*) * n);//二级指针,存放一级指针数组的地址
	for (int i = 0; i < n; i++)
	{
		a[i] = (int*)malloc(sizeof(int) * m);//将数组中的地址指向一个一维数组
	}
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			cin >> a[i][j];//一个一个的输入数组元素的值
		}
	}
	
	/*Print(a, n, m);*/
	
	if (GetPath(a, n, m, { 0,0 }))
	{
		stacks2;
		int num = s1.size();
		for (int i = 0; i