C++数据结构:排序(上)

目录

插入排序

(1)直接插入排序

(2)希尔排序

选择排序

(1)直接选择排序

(2)堆排序

冒泡排序

归并排序

---

插入排序

(1)直接插入排序

假若说我这边有一个数组为{9,8,7,6,5,4,3,2,1,0}我想将这个数组从逆序变为顺序排列,我们先说说直接插入排序是怎么排的,再来用代码实现

我们把扑克牌一张一张的从下面拿到手上,我们一边抽牌一边把手中的牌变为有序,直接插入排序就跟这种情况差不多

就是像这样的,我们开始将9看作一个有序的数组,然后我们将8插入进去,插入完之后,我们就将前两个数变成有序的了,然后我们再把8 9看成一个数组,将后面一个元素7插入进去,就变成有序的7 8 9依次进行这样的操作我们就将数组变成有序数组了

我们来说说代码

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n-1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				end--;
			}
			else {
				break;
			}
		}
		a[end + 1] = tmp;
	}
}
int main()
{
	int a[] = { 9,8,7,6,5,4,3,2,1,0 };
	int n = sizeof(a) / sizeof(int);
	for (int i = 0; i < (sizeof(a) / sizeof(int)); i++)
	{
		cout << a[i] << " ";
	}
	return 0;
}

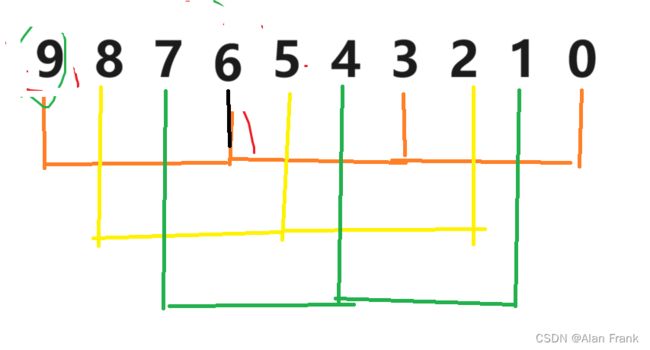
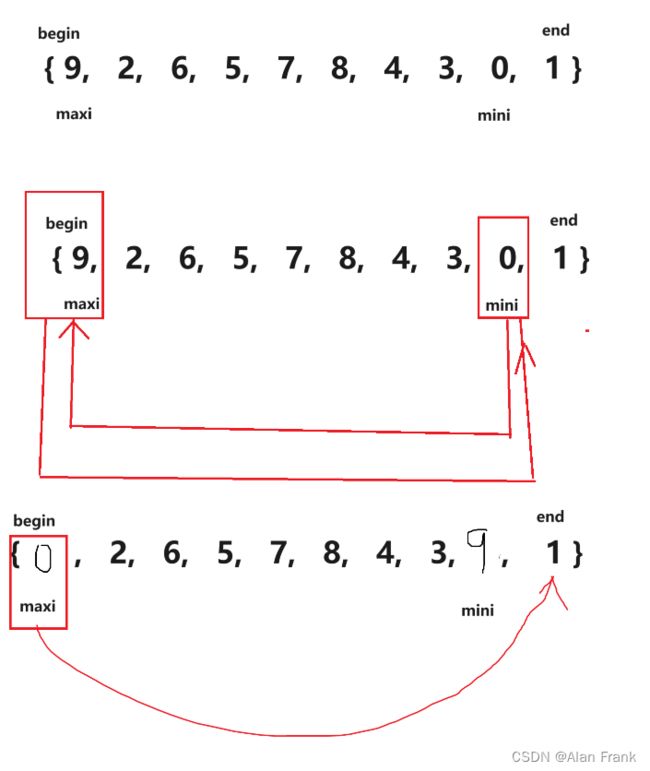
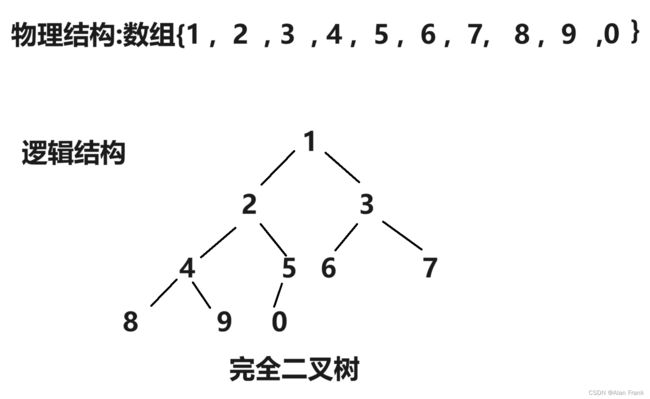
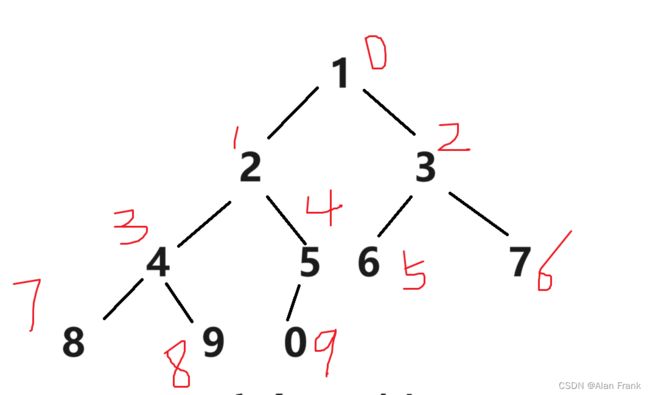
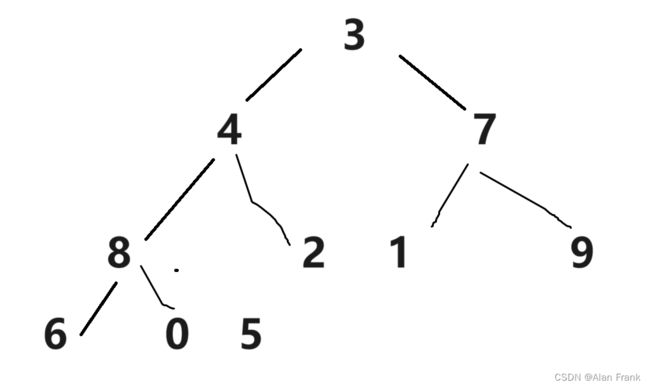
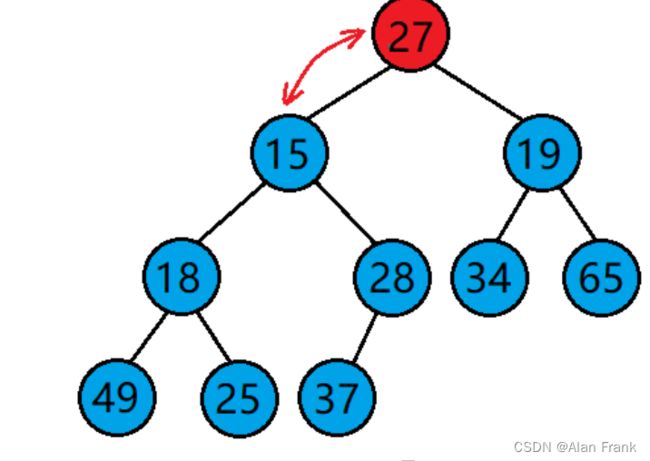
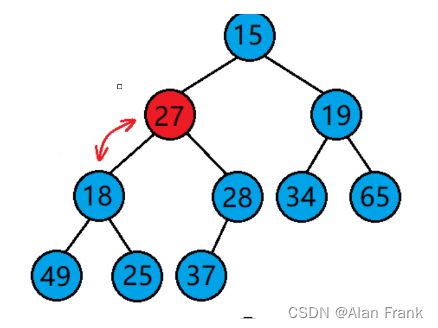
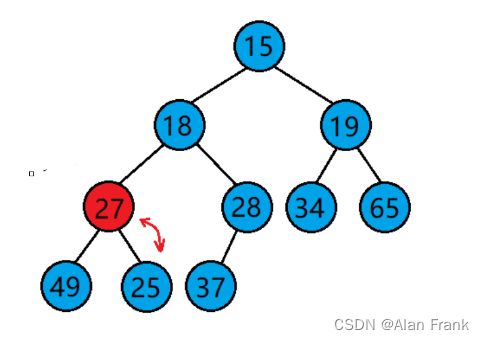
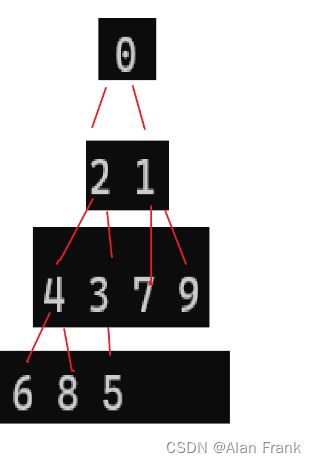
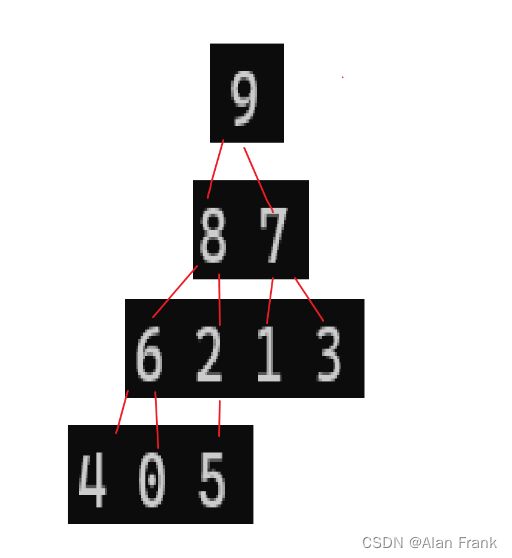
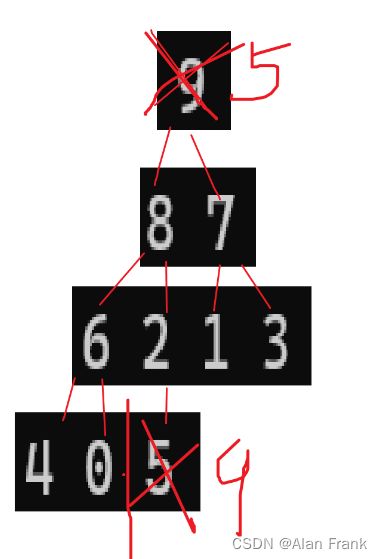
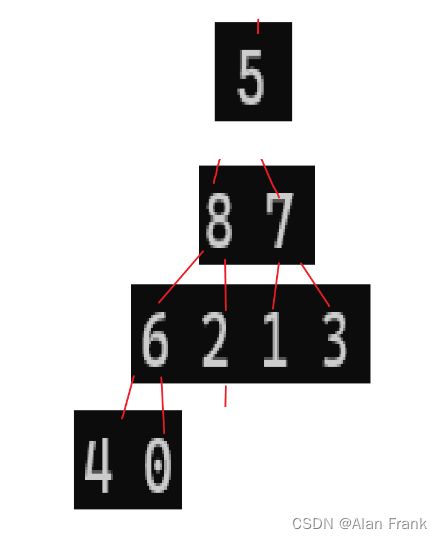
我们具体讲解一下代码,我们先拿第一次9里面放8来说,我们先把end放到我们指定数组的最后一个位置上就是9的位置,end+1自然就是我们插入进去的元素的位置,我们先拿一个tmp变量来保存end+1位置上的元素,因为我们比较完end和end+1位置上的元素之后,如果end上的元素比end+1上的元素大,end上的那个元素就会放到end+1上,会将end+1上的元素覆盖,我们先比较9和8,9比8大,9放到end+1的位置上,然后end向后面走去找下一个元素跟8比较但是后面没有了,那就把8放到end+1的位置上,强调一下是end+1,应为比较完end就向后面走了,相当于end+1的位置就空出来了(实际上是那个9),把8放进去第一次插入也就结束了.为什么i

因为n表示我们的数组的个数,实际最大索引为n-1,我们end是表示的有序数组中最后一个元素,所以end到n-2停止下来就行

(2)希尔排序

希尔排序其实是直接插入排序的一种优化排序,我们先来说一说直接插入排序最坏的情况,其实就是我上面提到了{9,8,7,6,5,4,3,2,1,0}数组整个是逆序的,让你排成顺序,第一个元素插入需要交换1次,第二个元素插入需要交换2次,.....,第n-1次元素插入进去需要交换n-1次,把他们加起来就是一个等差数列求和呀,(n-1)*(n-2)/2时间复杂度就是O(n^2),直接插入排序就会显得很是麻烦,效率很低,就出现了希尔排序

希尔排序怎么排的呢?我们就是对原始数组不断进行预排序,我们将间距为gap的元素看作是一组的,

就是像这样,我们把gap先来设置成3,我们就把9,6,3,0看作是一组的,将8,5,2看组是一组的,将7,4,1看组是一组的了,然后对他们每一组来进行排序,让后排完之后,我们将gap减小,再进行分组排序,当gap一直小到1的时候,其实就是直接插入排序了,但是这个时候经过前面一系列的预排序,我们将这个数组已经排成几乎有序的状态,再进行gap为1的排序效率就会很高.

代码实现

#include
using namespace std;
void ShellSort(int* a, int n)//希尔排序  
{
	int gap = n;
	while (gap >= 1)
	{
		gap = gap / 2;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0) {
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else {
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
	cout << count << endl;
}
int main()
{
	int a[] = { 9,8,7,6,5,4,3,2,1,0 };
	int n = sizeof(a) / sizeof(int);
	ShellSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < (sizeof(a) / sizeof(int)); i++)
	{
		cout << a[i]<<" ";
	}
	return 0;
}

一开始我们先将gap设置为数组的长度,进入while循环之后gap变为原来的二分之一,然后就相当于直接插入排序,但是要说一个特殊的地方就是循环变量i,从0开始不用说,结束是在n-gap-1的索引上结束,每回都是+1,多组数据一块排序.

选择排序

(1)直接选择排序

我们通过一个动图来看看什么是直接选择排序

假如说我现在有一个数组{2,6,5,7,8,4,9,3,0,1}我们用直接选择排序的方法来排序

我们先设定一个begin和end,在begin和end中找到一个最大的数和一个最小的数,让最小的数和begin交换位置,最大的数和end交换位置,然后交换完之后begin往后移动一个位置,end往前移动一个位置,当begin和end碰面的时候我们让他们停止下来,我们看看具体的代码实现

#include
using namespace std;
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void SelectSort(int* a,int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		int maxi = begin;
		int mini = begin;
		for (int i = begin; i <= end; i++)
		{
			if (a[maxi] < a[i])
			{
				maxi = i;
			}
			if (a[mini] > a[i])
			{
				mini = i;
			}
		}
		Swap(&a[begin], &a[mini]);
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}
int main()
{
	int a[] = { 2,6,5,7,8,4,9,3,0,1 };
	int n = sizeof(a) / sizeof(int);
	SelectSort(a, n);
	for(int i=0;i

但是有时候会出现问题,假如说我的数组是{ 9,2,6,5,7,8,4,3,0,1 },

出现的结果不是排好序的,而是

我画一张图,来看一看

因为mini指向的最小值会和begin上的元素进行交换,但是maxi对应的最大值正好在begin上,这样0就会跑到第一位上,9就会到原来0的位置上

maxi和mini对应的下标值不变,此时要是再将maxi上的位置放到end上,就相当于把0放到了end上

void SelectSort(int* a,int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		int maxi = begin;
		int mini = begin;
		for (int i = begin; i <= end; i++)
		{
			if (a[maxi] < a[i])
			{
				maxi = i;
			}
			if (a[mini] > a[i])
			{
				mini = i;
			}
		}
		Swap(&a[begin], &a[mini]);
		if (maxi == begin)//加这三行代码判断一下就行
		{
			maxi = mini;
		}
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}

如果begin和maxi重合,那我们在第一次交换玩之后就修改一下maxi指向,因为最小值和begin交换了,那我们就让maxi指向最小值的那个位置

(2)堆排序

堆排序逻辑结构是一个完全二叉树,物理结构上是一个数组

我们看看是怎么个事,用一个画图

我们在图中标注出元素在数组中的索引

通过观察父节点和子节点的索引之间的关系,我们可以得出:左孩子=父亲*2+1;右孩子=父亲*2+2

父亲 = (左孩子或者右孩子-1)/2   我们知道一个孩子就能求它的父亲

堆:分成大堆和小堆

大堆要求:树中所有的父亲都大于等于孩子

小堆要求:树中所有的父亲都小于等于孩子

我们把堆变成大堆和小堆之后不会将堆排成有序但是变成大堆之后根节点就是最大的了,变成小堆之后根节点就是最小的了

在进行排序之前我们先要去建堆(可以是大堆也可以是小堆),假如我们有一个数组{3,4,7,8,2,1,9,6,0,5},我们画出他的逻辑图,我们对这个树进行调整

先说一下向下调整算法  有一个前提:假如说我要建小堆,得要保证这个跟节点的左右子树都是小堆才能进行向下调整

27为根节点,他的左右子树都是小堆,我们可以向下调整,先找到左右孩子中较小的一个交换位置,然后交换完后如图

交换完之后我们接着找左右孩子中较小的一个然后进行交换,一直换到叶节点或者27放到了两个子节点都比它大的位置上去

这就是我们说的向下调整算法,一定要注意向下调整的前提:左右子树一定是堆(大堆或者小堆)

代码如下

#include
using namespace std;
void Swap(int* a, int* b)
{
	int tmp = 0;
	tmp = *a;
	*a = *b;
	*b = tmp;
}
void AjustDown(int* a, int n, int root)
{
	int parent = root;
	int child = parent * 2 + 1;
	while (child < n-1)
	{
		if (child + 1 && a[child + 1] < a[child])
		{
			child += 1;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else {
			break;
		}
	}
}

但是如果不是根节点的左右子树不是堆,那我们就不能直接使用向下调整算法了,那怎么办?

那我们就倒着去调,叶节点没有子节点,叶节点不用调,这就需要我们找到倒数的第一个有孩子的节点,也好找,孩子=2*父亲+1,倒过来我们知道孩子的小标为n-1,那么父亲就是(n-1-1)/2,然后找到了之后我们反着去向下调整,这样就能得到一个小堆或大堆

int main()
{
	int a[] = { 3,4,7,8,2,1,9,6,0,5 };
	//建堆
	int n = sizeof(a) / sizeof(int);
	for (int i = (n - 1-1) / 2; i >= 0; i--)
	{
		AjustDown(a, n, i);
	}
	for (int j = 0; j < n; j++)
	{
		printf("%d ", a[j]);
	}
	return 0;
}

得到结果是

我们来画一下它的逻辑图

说明我们把数据排成了小堆

如果说我们想搞成大堆,我们只要改一下向下调整的符号就行,上代码了很详细了已经

void AjustDown(int* a, int n, int root)
{
	int parent = root;
	int child = parent * 2 + 1;
	while (child < n-1)
	{
		if (child + 1 && a[child + 1] > a[child])
		{
			child += 1;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else {
			break;
		}
	}
}

如果说我要将我给的数组进行顺序排序的话,我们应该建大堆还是小队呢?很多人会想着建小堆,但是事实上是要建立一个大堆的,建小堆的话我们将最小值放到了根节点那,要是再接着调整的话,我们还需要再次建立一个堆,这个堆不包括上个树的根节点,然后进行向下调整找到最小的,这样的话不是不行,会让我们的时间复杂度大大增加

想要进行顺序排序,那就建立一个大堆

然后我们将9和最后一个元素就是5交换位置

交换完位置之后,我们发现最大的就已经放到数组的末尾了.我们接着对前n-1进行向下调整找到次大的数

前n-1个元素形成的堆

我们进行向下调整后,得到

然后交换位置后,将数组n-1再-1重复上面的操作就可以得到顺序的结果了

while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AjustDown(a, end, 0);
		end--;
	}
	for (int j = 0; j < n; j++)
	{
		printf("%d ", a[j]);
	}

冒泡排序

#include
using namespace std;
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void BulleSort(int *a,int n)
{
	for (int j = 0; j < n; j++)
	{
		for (int i = 0; i < n - j-1; i++)
		{
			Swap(&a[i], &a[i + 1]);
		}
	}
}
int main()
{

	int a[] = { 9,8,7,4,5,6,3,2,1,0 };
	int n = sizeof(a) / sizeof(int);
	BulleSort(a, n);
	for (int i = 0; i < n; i++)
	{
		cout << a[i] << " ";
	}
	return 0;
}

冒泡排序实际上就是前后交换,要想排升序,就是把大的交换到前面

冒泡排序是可以进行优化的

#include
using namespace std;
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void BulleSort(int *a,int n)
{
	
	for (int j = 0; j < n; j++)
	{
		int flag = 0;
		for (int i = 0; i < n - j-1; i++)
		{
			Swap(&a[i], &a[i + 1]);
			flag = 1;
		}
		if (flag == 0)
		{
			break;
		}
	}
}
int main()
{

	int a[] = { 9,8,7,4,5,6,3,2,1,0 };
	int n = sizeof(a) / sizeof(int);
	BulleSort(a, n);
	for (int i = 0; i < n; i++)
	{
		cout << a[i] << " ";
	}
	return 0;
}

我们想设置一个flag变量,如果冒着冒着发现冒其中一趟的时候,没有进行交换(说明这个时候数据已经有序了,不用再接着冒了)flag仍然等于0,那就直接跳出循环就得了

归并排序

#include
#include
#include
#include
#include
using namespace std;
int a[] = { 7,8,9,6,5,4,1,2,3,0 };
int* help = (int*)malloc(sizeof(int) * (sizeof(a) / sizeof(int)));
void merage(int a[], int begin, int mid, int end)
{
	int left = begin;
	int right = mid + 1;
	int current = begin;
	for (int i = 0; i <= end; i++)
	{
		help[i] = a[i];
	}
	while (left <= mid && right <= end)
	{
		if (help[left] > help[right])
		{
			a[current] = help[left];
			left++;
			current++;
		}
		else if (help[left] <= help[right])
		{
			a[current] = help[right];
			right++;
			current++;
		}
	}
	while (left <= mid)
	{
		a[current] = help[left];
		left++;
		current++;
	}
	while (right <= end)
	{
		a[current] = help[right];
		right++;
		current++;
	}
}
void merageSort(int a[], int begin, int end)
{
	if (begin < end)
	{
		int mid = (begin + end) / 2;
		merageSort(a, begin, mid);
		merageSort(a, mid + 1, end);
		merage(a, begin, mid, end);
	}
}
int main()
{
	int n = sizeof(a) / sizeof(int);
	merageSort(a, 0, n - 1);
	for (int i = 0; i < n; i++)
	{
		cout << a[i] << " ";
	}
	return 0;
}