计数排序 详解 C代码

1.计数排序作为一个排序算法有以下几个特点:

(1)不基于比较

(2)稳定排序

(3)时间复杂度O(n)

(4)只能用在数据范围不大的场景(这个问题在举例以后会在讨论)

2.算法思路

        (1) 假设有 10 个学生,分数区间在 0~9 ,对应下图原数组

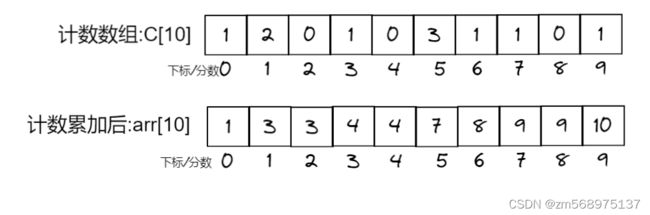
        (2) 现在数组下标为 0~9, 学生分数区间也是 0~9, 我们暂时先将 分数 对应成 下标 创建一个新数组C[10],然后将10个同学的分数,以相同分数计数,并将计数后的结果 填入到 新数组中去,如下图

我们看下计数数组C是什么意思,

C[0] = 1,意思是:分数为0的学生有 1 个

C[1] = 2,意思是:分数为1的学生有 2 个

.....以此类推

C[9] = 1,意思是:分数为9的学生有 1 个

        (3) 现在我们需要从左往右,依次保留前一次累加的值在向后 累加 ,如下图

 我们来看下 计数累加后的新数组 arr[10],

arr[1] = C[0] + C[1] = 1 + 2 =3 

arr[2] = arr[1] +C[2] = C[0] + C[1] + C[2] = 1 + 2  + 0 = 3

arr[3] = arr[2] +C[3] = C[0] + C[1] + C[2] +C[3] = 1 + 2 + 0 + 1 = 4

.......以此类推

arr[9] = C[0] + ...+C[9] = 10

(4)有了arr数组后,我们就可以排序了,思路是:

        1)首先创建一个 和 原数组 一样大小的数组:dst,用来存储排序后的结果

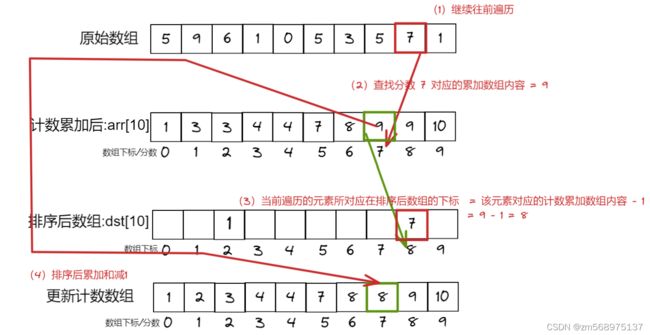
        2)从原数组的最后1个数据往前遍历,比如开始要排序的数据是数组的最后一个元素  1 

        3)然后将 1 作为arr数组中的下标并找其对应的值,即arr[1] = 3

        4)将找到的值 减 1 就是最终在排序后数组的下标 ,即 dst[3-1]=1,得到 dst[2] = 1

        5)将arr数组对应的值减1,即arr[1]=3-1=2

        6)开始循环向前遍历

        运行流程如下图: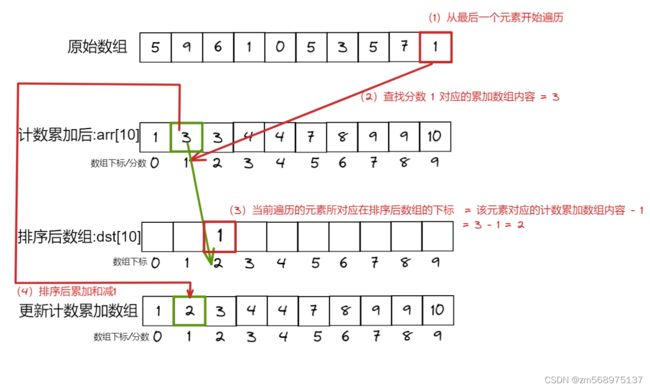

第一次循环

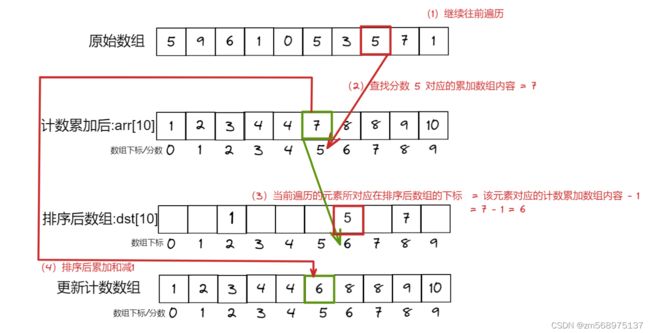
 第二次循环

 第三次排序

后面以此类推即可...........

实现代码如下:

#include 
using namespace std;

void count_sort(int* a, int n, int* dst)
{
	//对每个分数进行计数
	int* arr = new int[n] {0};
	for (int i = 0; i < n; i++)
	{
		int point = a[i];
		arr[point]++;
	}
	//累加求和
	for (int i = 1; i < n; i++)
		arr[i] += arr[i-1];
	//开始从最后一个元素排序
	for (int i = n - 1; i >= 0; i--)
	{
		//确定排序后的索引位置
		int sorted_index = arr[a[i]] - 1;
		//赋值
		dst[sorted_index] = a[i];
		//计数-1
		arr[a[i]] --;
	}
	delete[] arr;
	arr = nullptr;
}

int main()
{
	int a[10] = { 5,9,6,1,0,5,3,5,7,1 };
	for (const auto& val : a)
		cout << val << ",";
	cout << endl;
	int dst[10] = {0};

	count_sort(a, 10, dst);

	for (const auto& val : dst)
		cout << val << ",";
	return 0;
}

大佬们应该发现了,上述代码有点问题,开始为了便于理解,对数据区间的选择做了一些假设,如果我们将数据想的复杂一些,比如:

(1)如果我们的数据区间不是从0开始,比如我们要排序的是50~150分区间同学的成绩,那又该如何呢?

(2)我们排序的前提是需要创建一个计数数组,数组的大小是数据区间的大小,那如果数据的区间是1W或者更大,我们就得创建这么大的数组么?

针对上述的问题,我们需要进行代码的优化

优化思路:

(1)先找到数据的最小,最大值,即min和max

(2)将计数数组arr的大小设置成 max-min+1

(3)后续定位计数数组arr的下标的方式为 : 当前遍历的分数 - min

修改代码如下:

#include 
#include 
#include 
using namespace std;

void count_sort(int* a, int n, int* dst)
{
	//找到最小和最大值
	int min_point = *std::min_element(a, a + n);
	int max_point = *std::max_element(a, a + n);
	int point_range = max_point - min_point + 1;
	//根据区间大小分配arr的数组大小
	int* arr = new int[point_range] {0};
	//对每个分数进行计数
	for (int i = 0; i < n; i++)
	{
		int point = a[i];
		arr[point - min_point]++;
	}
	//累加求和
	for (int i = 1; i < point_range; i++)
		arr[i] += arr[i - 1];
	//开始从最后一个元素排序
	for (int i = n - 1; i >= 0; i--)
	{
		//确定排序后的索引位置
		int sorted_index = arr[a[i] - min_point] - 1;
		//赋值
		dst[sorted_index] = a[i];
		//计数-1
		arr[a[i] - min_point] --;
	}
	delete[] arr;
	arr = nullptr;
}

int main()
{
	std::default_random_engine e;
	std::uniform_int_distribution range(50, 150); 
	int a[10] = {0};
	cout << "原始数组:" << endl;
	for (int i = 0; i < 10; i++)
	{
		a[i] = range(e);	//产生50~150的随机数
		cout << a[i] << ",";
	}
	cout << endl;
	int dst[10] = { 0 };

	count_sort(a, 10, dst);
	cout << "排序后:" << endl;
	for (const auto& val : dst)
		cout << val << ",";
	return 0;
}

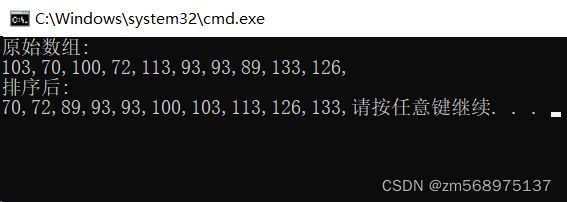
运行结果如下:

 

好了,最后我们在来讨论一下,为什么说计数排序 适用 在数据范围不大的场景

看了上述的实现以后我们思考以下两种假设情况:

        (1)我们有1000W个学生,每个学生的成绩范围是0~150 分

        (2)我们有1000W个学生,每个学生的成绩范围是0~1024w 分

如果我们对第一种情况使用计数排序,那么计数数组的大小=150 Bytes

如果我们对第二种情况使用计数排序,那么计数数组的大小=97 MB

数据范围越大,申请的空间 和 累加计数的次数都会往上增加,反而没有其他排序快

最后总结一下:

(1)计数排序之所以从后向前遍历,因为这样才能让原数组中靠后的数据,在排序后的数组中也靠后,达到稳定排序的目的

(2)计数排序不适用于 数据范围 比 待排序数据 大 很多的场景

(3)只能用于非负整数的数据范围(因为数组下标只能是整数)

        1)如果是小数,如1.81 , .2.35,可以将数据同时乘以1000之类的转换成整数

        2)如果是其他类型,要在不改变其相对大小的情况下,转换成非负整数