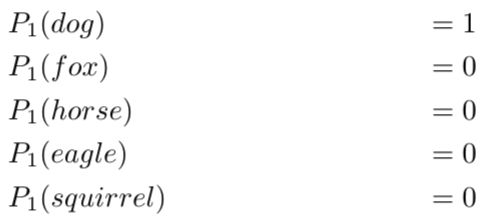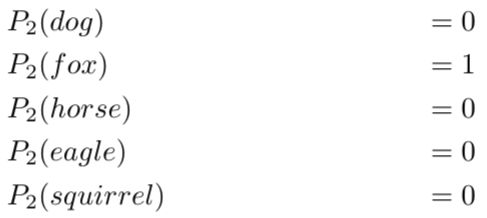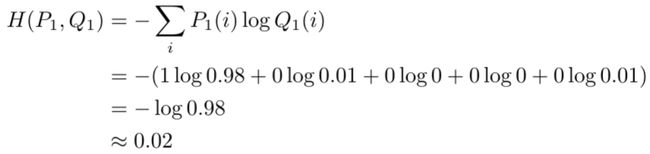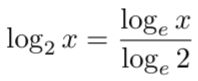为什么要用“交叉熵”做损失函数
大家好啊,我是董董灿。
今天看一个在深度学习中很枯燥但很重要的概念——交叉熵损失函数。
作为一种损失函数,它的重要作用便是可以将“预测值”和“真实值(标签)”进行对比,从而输出 loss 值,直到 loss 值收敛,可以认为神经网络模型训练完成。
那么这个所谓的“交叉熵”到底是什么,为什么它可以用来作为损失函数呢?
1、熵与交叉熵
“交叉熵”包含了“交叉”和“熵”这两部分。
关于“熵”的描述在理解熵的本质一文中有更详细的说明。总的来说,熵可以用来衡量一个随机变量的不确定性,数学上可表示为:
H(i) = - ∑ P(i) * log(P(i))
对于上面的公式,我们稍微变一下形,将负号和 log(P(i)) 看做一个变量,得到:
PP(i) = -log(p(i))
那么熵的公式就可以写作:
H(i) = ∑ P(i) * PP(i)
此时熵的公式中,P(i) 和 PP(i) 是服从相同的概率分布。因此,熵H(i)就变成了事件 PP(i) 发生的数学期望,通俗理解为均值。
熵越大,表示事件发生的不确定性越大。
而交叉熵是用于比较两个概率分布之间的差异,对于两个概率分布 P 和 Q 而言,交叉熵定义为:
H(i) = ∑ P(i) * Q(i)
此时,P(i) 和 Q(i) 服从两种不同的概率分布,交叉熵的“交叉”就体现在这。
其中 P(i) 为真实分布,也就是训练过程中标签的分布;Q(i) 为预测分布,也就是模型每轮迭代输出的预测结果的分布。
交叉熵越小,表示两个概率分布越接近。
从而模型预测结果就越接近真实标签结果,说明模型训练收敛了。
关于更细节的数学原理,可以查看熵的本质,不过我们也可以不用深究,理解上述结论就可以。
2、交叉熵作为损失函数
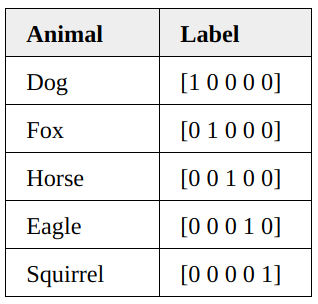
假设有一个动物图像数据集,其中有五种不同的动物,每张图像中只有一只动物。
我们将每张图像都使用 one-hot 编码来标记动物。对one-hot编码不清楚的可以移步这里有个你肯定能理解的one-hot。
上图是对动物分类进行编码后的表格,我们可以将一个one-hot 编码视为每个图像的概率分布,那么:
第一个图像是狗的概率分布是 1.0 (100%)。
对于第二张图是狐狸的概率分布是1.0(100%)。
以此类推,此时,每个图像的熵都为零。
换句话说,one-hot 编码标签 100% 确定地告诉我们每张图像有哪些动物:第一张图片不可能 90% 是狗,10% 是猫,因为它100%是狗。
因为这是训练的标签,是固定下来的确定分布。
现在,假设有一个神经网络模型来对这些图像进行预测,在神经网络执行完一轮训练迭代后,它可能会对第一张图像(狗)进行如下分类:
该分类表明,第一张图像越 40%的概率是狗,30%的概率是狐狸,5%的概率是马,5%的概率是老鹰,20%的概率是松鼠。
但是,单从图像标签上看,它100%是一只狗,标签为我们提供了这张图片的准确的概率分布。
那么,此时如何评价模型预测的效果呢?
我们可以计算利用标签的one-hot编码作为真实概率分布 P,模型预测的结果作为 Q 来计算交叉熵:
结果明显高于标签的零熵,说明预测结果并不是很好。
继续看另一个例子。
假设模型经过了改良,在完成一次推理或者一轮训练后,对第一张图得到了如下的预测,也就是说这张图有98%的概率是狗,这个标签的100%已经差的很少了。
我们依然计算交叉熵:
可以看到交叉熵变得很低,随着预测变得越来越准确,交叉熵会下降,如果预测是完美的,它就会变为零。
基于此理论,很多分类模型都会利用交叉熵作为模型的损失函数。
在机器学习中,由于多种原因(比如更容易计算导数),对数 log 的计算大部分情况下是使用基数 e 而不是基数 2 ,对数底的改变不会引起任何问题,因为它只改变幅度。
最近开通另一个计算机视觉从入门到调优的专栏,感兴趣的小伙伴可以查看:计算机视觉从入门到调优