Morris遍历的图示理解以及代码实现
文章目录
- Morris遍历的图示理解以及代码实现
-
- 1、遍历规则
- 2、复杂度分析
- 3、代码实现以及分析
- 4、Morris遍历实现前中后序遍历
Morris遍历的图示理解以及代码实现
1、遍历规则
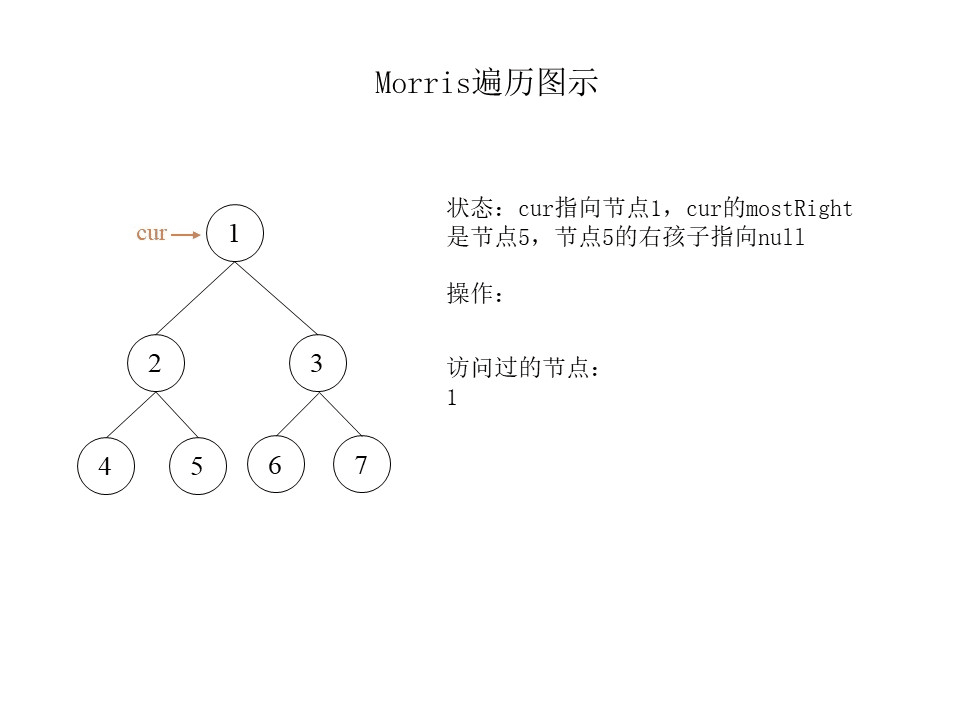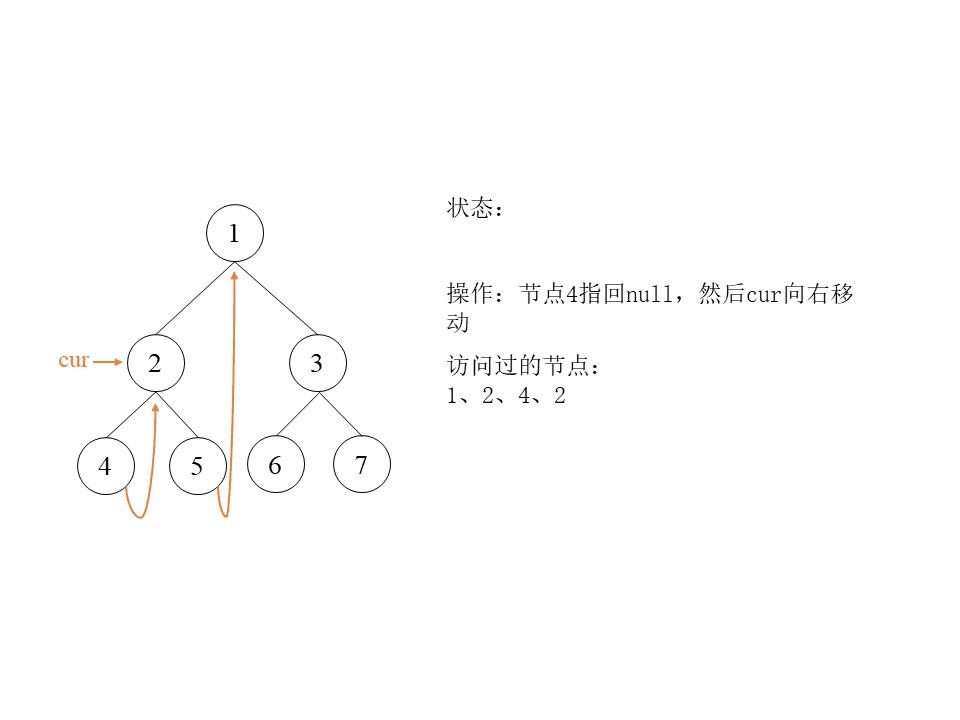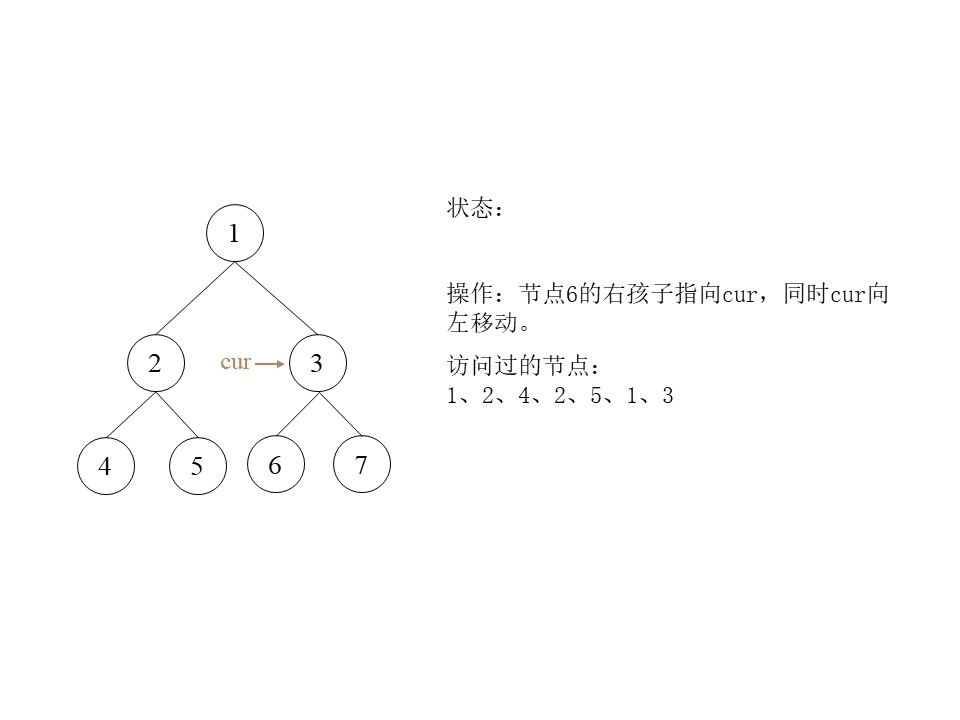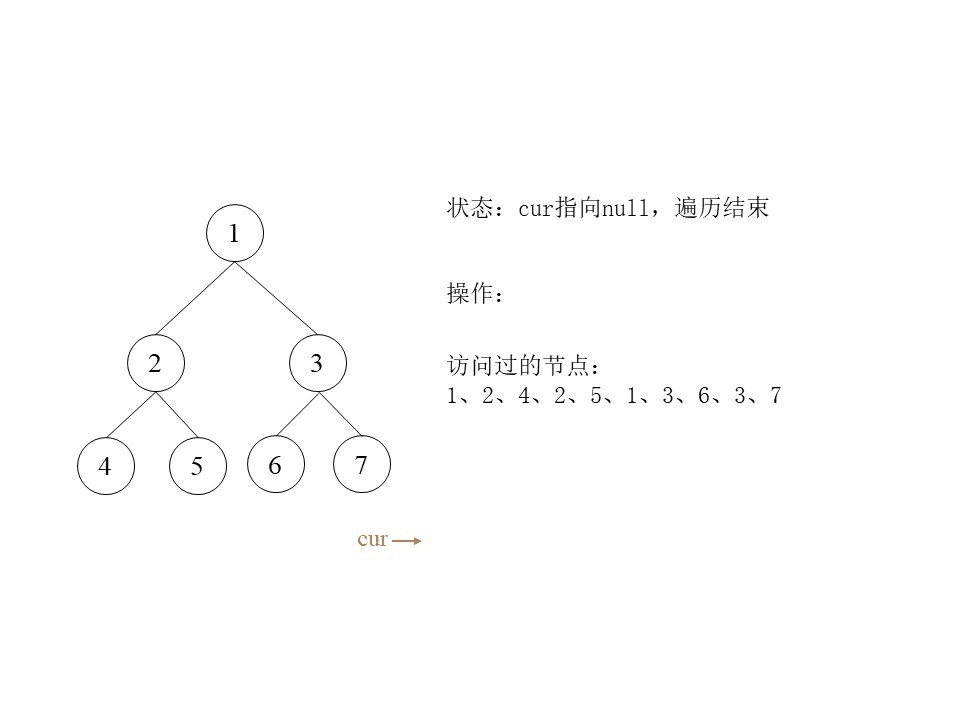
假设当前正在遍历的节点是cur,那么cur的移动规则如下:
- 如果cur没有左孩子,则cur向右移动,即
cur = cur.right。 - 如果cur有左孩子,找到cur左子树上最右边的节点,将这个节点记为mostRight,根据mostRight的情况继续分为下面两种情况:
- 如果mostRight的右孩子为null,则让mostRight的右孩子指向cur,然后cur向左移动,即
cur = cur.left。 - 如果mostRight的右孩子指向cur,则让mostRight的右孩子指回null,然后cur向右移动,即
cur = cur.right。
- 如果mostRight的右孩子为null,则让mostRight的右孩子指向cur,然后cur向左移动,即
2、复杂度分析
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 1 ) O(1) O(1)。这里就体现出了Morris遍历的神奇的地方,二叉树的递归和非递归遍历都要借助栈来实现遍历整棵树,所以空间复杂度为 O ( h ) O(h) O(h),其中 h h h 指的是二叉树的最大高度,但是Morris遍历没有用到栈,仅仅是使用节点的引用来实现遍历整棵树,所以空间复杂度为 O ( 1 ) O(1) O(1)。
解释一下为什么递归和非递归遍历需要用到栈。递归写法中虽然没有显式用到栈,但是本质上还是用栈实现的。因为二叉树中只有父节点指向子节点的指针,遍历的过程中,如果想从子节点回到父节点怎么办,这里使用栈这种数据结构,先把父节点入栈,访问子节点,访问完成后,父节点出栈,就相当于从子节点回到了父节点。
Morris遍历也需要遍历整棵二叉树,那么Morris遍历中是如何做到从子节点回到父节点的呢。从Morris遍历的规则可以知道,Morris遍历是通过mostRight的右孩子的指向来从子节点回到父节点的。
3、代码实现以及分析
public class MorrisTraversal {
public static void morrisTraversal(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
if (cur.left == null) {
cur = cur.right;
} else {
// 首先找到mostRight的位置
mostRight = cur.left;
while (mostRight.right != null
&& mostRight.right != cur) {
mostRight = mostRight.right;
}
// 根据mostRight的右孩子指向谁,分为两种情况
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
} else if (mostRight.right == cur) {
mostRight.right = null;
cur = cur.right;
}
}
}
return;
}
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
简要解释:根据上面的动态图示,可以看到cur指针在遍历完成之后指向null,所以代码中第一层循环while (cur != null){}的循环体内是对二叉树的完整遍历。基本是按照Morris遍历的规则来组织代码的,其中可能会有疑惑的地方是在寻找mostRight位置的循环条件while (mostRight.right != null && mostRight.right != cur) {},因为mostRight的右孩子的指向可能有两种情况,如下所示:
第一种情况:cur指针第一次指向节点1,此时的mostRight是节点5,节点5的右孩子指向null。

第二种情况:cur指针第二次指向节点1,第二次的含义是遍历完了节点1的左子树,通过图中橘黄色的引用回到了节点1,所以是第二次指向。此时mostRight是节点5,节点5的右孩子指向cur。

4、Morris遍历实现前中后序遍历
给出Morris遍历的前中后序遍历代码之前,先理解一下二叉树的递归遍历代码。如下所示:
public class Solution {
public void treeTraversal(TreeNode root) {
if (root == null) {
return;
}
// 1 {code block}
treeTraversal(root.left);
// 2 {code block}
treeTraversal(root.right);
// 3 {code block}
}
}
二叉树递归遍历的前中后序遍历非常相似,原因就在于上述遍历代码,对于root这个节点,一共访问了三次,分别是注释标出来的三个地方,假如注释的方法有相关代码,必定会得到执行,所以把访问当前节点的代码,即System.out.print(root.val + " "),分别放在注释的三个地方就可以实现对二叉树的前、中、后序遍历。
递归遍历中对每个节点都访问三次,那么Morris遍历中对每个节点访问几次呢?上面的图示中,遍历完成之后,得到的遍历序列是1、2、4、2、5、1、3、6、3、7,可以发现有左孩子的节点1、2、3遍历了两次(上面分析代码的时候有图示讲解了为什么会遍历两次),对于没有左孩子的节点4、5、6、7遍历了一次,因为这四个节点没有左孩子,也就不会遍历到左子树上去,所以只会遍历一次。这段分析可以解释为什么Morris遍历的时间复杂度是 O ( n ) O(n) O(n) ,因为每个节点最多被遍历两次。
接下来就可以分析Morris遍历的前中后序遍历了。
1)前序遍历:第一次遍历到某个节点的时候,将其打印输出。
public class MorrisTraversal {
public static void morrisPre(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
if (cur.left == null) {
// 打印输出
System.out.print(cur.val + " ");
cur = cur.right;
} else {
mostRight = cur.left;
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
// 打印输出
System.out.print(cur.val + " ");
cur = cur.left;
} else if (mostRight.right == cur) {
mostRight.right = null;
cur = cur.right;
}
}
}
return;
}
}
代码中有两个地方含有打印输出语句。第一处是在cur没有左子树的时候,直接打印cur,然后cur向右移动;第二处是在cur有左子树,在cur向左移动之前,此时是第一次遍历当前节点,故打印cur。
2)中序遍历:
public class MorrisTraversal {
public static void morrisIn(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
if (cur.left == null) {
// 打印输出
System.out.print(cur.val + " ");
cur = cur.right;
} else {
mostRight = cur.left;
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
} else if (mostRight.right == cur) {
mostRight.right = null;
// 打印输出
System.out.print(cur.val + " ");
cur = cur.right;
}
}
}
System.out.println();
return;
}
}
中序遍历的两处打印输出语句,一处是在cur没有左子树的时候,直接打印cur;第二处是在cur有左子树,把当前节点的左子树遍历完了,cur向右移动之前,此时是第二次遍历到该节点,打印cur。
3)后序遍历:
Morris中,对一个节点最多只会遍历两次,那么怎么做到后序遍历呢?做法是这样的:对于没有左子树的节点,这些节点只会遍历一次,不用关心这些节点。对于含有左子树的节点,这些节点会被遍历两次,在第二次遍历的时候逆序打印左子树的右边界。最后在函数退出之前再单独逆序打印整棵树的右边界。
下图展示了一个节点A的左子树的右边界,逆序打印的话就是E、D、C、B。因为此时是第二次遍历到节点A,所以会存在节点E(此时的mostRight)的右孩子指向节点A的指向,但是代码中先将节点E的右孩子置为null,之后再打印的。

如何做到逆序打印呢?做法是类似链表的翻转,翻转之后再把指向调整回来即可。
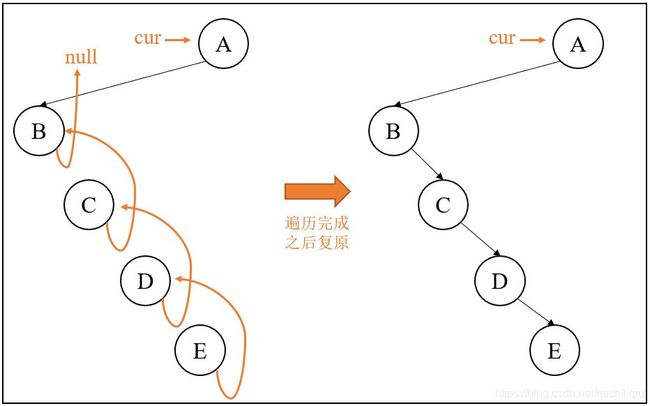
代码如下:
public class MorrisTraversal {
public static void morrisPost(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
if (cur.left == null) {
cur = cur.right;
} else {
mostRight = cur.left;
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
} else if (mostRight.right == cur) {
mostRight.right = null;
// 逆序打印cur左子树的右边界
printEdge(cur.left);
cur = cur.right;
}
}
}
// 逆序打印整棵树的右边界
printEdge(root);
System.out.println();
return;
}
private static void printEdge(TreeNode node) {
TreeNode tail = reverseEdge(node);
TreeNode cur = tail;
while (cur != null) {
System.out.print(cur.val + " ");
cur = cur.right;
}
reverseEdge(tail);
}
private static TreeNode reverseEdge(TreeNode node) {
TreeNode pre = null;
TreeNode cur = node;
TreeNode next = null;
while (cur != null) {
next = cur.right;
cur.right = pre;
pre = cur;
cur = next;
}
return pre;
}
}
参考资料:牛客网左老师算法课程