基于CUDA的Transformer Encoder并行化

　　写在前面：视觉Transformer模型的研究使得深度学习在分类、目标检测和语义分割等视觉任务上取得了非常好的应用，然而，因为其模型参数量大的特点，训练和推理的速度都受到了严峻的挑战，因此，并行化视觉Transformer模型具有很大的意义。本文首先根据对视觉Transformer模型的结构分析，尝试对Transformer Encoder部分进行基于CUDA C编程的并行化设计。然后，根据Transformer Encoder的结构将其分成一个个小的算子，基于CUDA C代码对这些算子实现了并行化的设计。最后，对实现的Transformer Encoder CUDA C并行化代码在RTX 3050上进行了测试。希望能给使用CUDA做算子开发小项目的你一点启示和帮助。

---

文章目录

Vision Transformer模型简单回顾

Transformer Encoder结构（以ViT-B/16为例）

层归一化（Layer Norm）

多头注意力机制（Multi-Head Attention）

Dropout/DropPath

设计过程

LayerNorm和残差结构并行化

Multi-Head Attention并行化

MLP Block并行化

实验

实验环境

实验过程和数据

总结

---

Vision Transformer模型简单回顾

　　2019年开始，自然语言处理（NLP）领域抛弃了循环神经网络（RNN）序列依赖的问题，开始采用Attention is All you need的Transformer结构，其中的Attention是一种可以让模型专注于重要的信息并能够充分学习和吸收的技术。在NLP领域中，伴随着各种语言Transformer模型的提出使得多项语言处理任务的精度和模型深度开始飞速提升。由于基于Transformer的预训练语言模型非常成功，研究者开始探索其在视觉领域的应用。2020年10月，Google创新性的设计了用于分类的Vision Transformer模型—ViT。此后视觉Transformer模型的研究进入了快车道。下图1是原论文中作者给出的关于Vision Transformer的模型总体框架图，

图1 Vision Transformer模型总体框架图

　　从图1中可以看出，Vision Transformer模型主要由三部分组成：第一部分为Linear Projection of Flattened Patches，也被称为Embedding层，主要用于将输入的图片数据转化为适合Transformer结构处理的形式。第二部分为Transformer Encoder部分，它是整个ViT模型的核心板块，在图1右侧给出了更加详细的结构，它主要由层归一化（Layer Norm）、多头注意力机制（Multi-Head Attention）、Dropout/DropPath、MLP Block四部分组成用于学习输入图像数据的特征。第三部分为MLP Head，它是最终用于分类的层结构。

本设计主要面向Transformer Encoder并行化，下面重点介绍一下Transformer Encoder结构。

Transformer Encoder结构（以ViT-B/16为例）

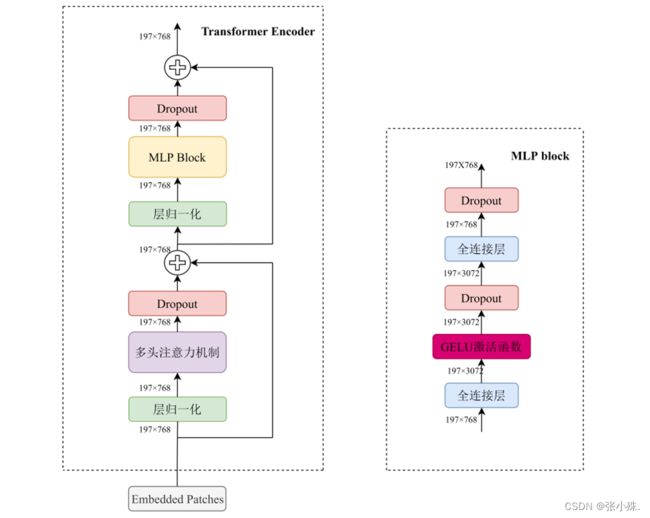
　　Transformer Encoder其实就是将Encoder Block 重复堆叠L次，Encoder Block结构图如下图2所示，主要由层归一化（Layer Norm）、多头注意力机制（Multi-Head Attention）、Dropout/DropPath、MLP Block四部分组成。

图2 Transformer Encoder结构图

层归一化（Layer Norm）

　　这是一种主要针对NLP领域提出的归一化方法，这里是对每个token进行归一化处理。目前的归一化层主要有BN、LN、IN、GN和SN五种方法，它解决了深度神经网络内部协方差偏移问题，是一种将深度神经网络之间的数据进行归一化的算法，使得深度学习的训练过程中梯度变化趋于稳定，从而使网络在训练时达到快速收敛的目的。将输入的图像shape记为[N, C, H, W]，这些方法的主要不同之处是，BatchNorm是在Batch上进行的，对NHW做归一化，对于较小的Batch Size没有太大的作用；LayerNorm是在通道方向上进行的，对CHW归一化，对RNN有很大的作用；InstanceNorm是在图像的像素上进行的，对HW做归一化，主要用在风格化迁移等方面；GroupNorm首先将Channel进行分组，然后再做归一化；SwitchableNorm是将BN、LN、IN结合并给予权重，让网络自己去学习归一化层应当使用的方法。

多头注意力机制（Multi-Head Attention）

　　通过多个注意力机制的并行组合，将独立的注意力输出串联起来，预期维度得到线性地转化。直观看来，多个注意头允许对序列的不同部分进行注意力运算。

Dropout/DropPath

　　在学习深度学习模型时，由于模型的参数过多、样本数量过少，导致了模型的过度拟合。在神经网络的训练中，常常会碰到一些问题。该方法具有较低的训练数据损失，具有较高的训练准确率。但是，测试数据的损失函数比较大，导致预测的准确性不高。

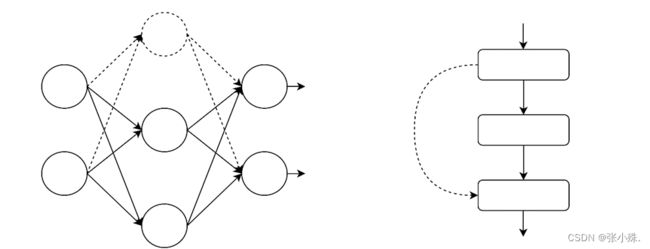
　　Dropout能在一定程度上减轻过度拟合，并能在某种程度上实现正规化。其基本原理是：在前向传播前进的过程中，使一个神经元的激活值以 p的概率不能工作，这在下面的图5中可以看到。停止工作的神经元用虚线表示，与该神经元相连的相应传播过程将不在存在。这使得模型更加一般化，因为它不会依赖于一些局部特征。

　　DropPath类似于Dropout，不同的是Dropout 是对神经元随机“失效”，而DropPath是随机“失效”模型中的多分支结构。例如如下图3右图所示，若x为输入的张量，其通道为[B,C,H,W]，那么DropPath的含义为一个Batch_size中，在经过多分支结构时，随机有drop_prob的样本，不经过主干，而直接经过分支（图中虚线）进行恒等映射。这在一定程度上使模型泛化性更强。

图3 Dropout和DropPath示意图

MLP Block

　　如图2右侧所示，MLP Block由全连接层、GELU激活函数、Dropout组成，以ViT-B/16为例，第一个全连接层会把输入节点个数翻4倍（197, 768）—> （197, 3072），第二个全连接层会还原回原节点个数（197, 3072）—> （197, 768）。

设计过程

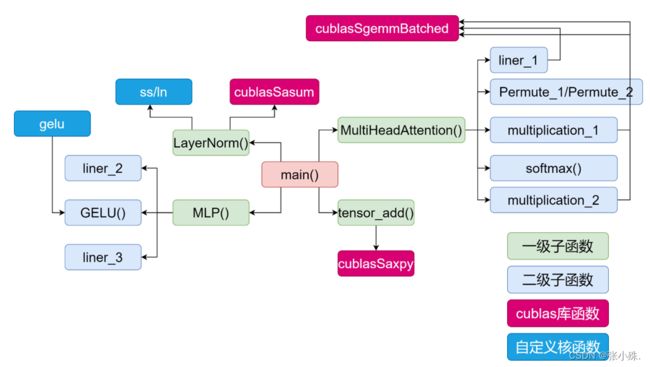
　　基于CUDA C编程根据Transformer Encoder的结构和特性对其实现并行化推理。对于Transformer Encoder结构，前文中已经分析过，它是由层归一化、多头注意力机制和MLP block组成的，因此，本文的设计也是逐一对其使用CUDA C编程实现并行化。其整体框架图如下图4所示。

图4 整体设计框架

LayerNorm和残差结构并行化

　　对于LayerNorm来说，它根据输入的tensor进行一系列的计算然后输出，并不改变tensor的维度信息，具体的，例如输入一个B*M*N的tensor张量，我们需要对每一个Batch的数据即M*N进行一系列计算（先求的这些数据的平均值和方差），然后使用式（2-4）进行层归一化计算。所以本文的对于Layer Norm的并行化思路具体如下。

　　首先，对于张量的形式，我们使用Vector进行存储，如下代码所示

std::vector> tensor(batch_count, std::vector(M * N));

　　这样我们就可以依次对每一个batch的数据进行操作，然后，我们需要先求的M*N数据的均值和方差，核心代码如下所示：

//先求和
cublasSasum(handle, 197 * 768, d_A[i], 1, &sum);
//求方差
ss << <160, 1024 >> > (d_A_copy[i], 197 * 768, sum / (197 * 768));
cublasSasum(handle, 197 * 768, d_A_copy[i], 1, &S);

　　如上代码所示，本文首先根据cublas库中的cublasSasum函数，实现每一个batch数据的求和，根据求和的结果sum很容易可以知道均值，然后使用设计的ss核函数来求得每一个数据减去均值的值存储在d_A_copy[i]中，最后使用cublas库中的cublasSasum函数对d_A_copy[i]求和得到方差S。ss核函数代码如下：

_global__ void ss(float* x, int n, float avg) {
    int ix = threadIdx.x + blockDim.x * blockIdx.x;
    if (ix < n)
        x[ix] = pow(x[ix] - avg, 2);
}

　　得到均值和方差之后，我们国家LN的计算方法设计核函数ln来实现最后的并行化过程，调用代码如下所示：

ln << <160, 1024 >> > (d_A[i], 197 * 768, sum / (197 * 768), S );

　　ln内核代码如下：

__global__ void ln(float* x, int n, float avg, float S) {
    int ix = threadIdx.x + blockDim.x * blockIdx.x;
    if (ix < n)
        x[ix] = (x[ix]-avg)/sqrt(S+ 1e-5);
}

　　这样我们便实现了layerNorm的并行化。

　　对于残差结构的并行化，它实质上是两个tensor相加的过程，在具体的推理过程中，分成两路，一路经过一系列的结构，一路不经过，最后两路相加。具体实现的过程中，本文定义了一个tensor_copy，记录每一次分路之前的tensor值，然后再相加的地方实现tensor_copy和tensor的相加，在代码中，我们使用了cublas库中的cublasSaxpy函数实现两个tensor的相加。

　　同时，本文注意到对于tensor相加来说，其本身的计算量就不是很高，如果逐个批次相加，其内核函数的开销将占用很大一部分时间，因此，本文首先将二维的vector张量转化为一维，然后实现相加，核心代码如下：

cublasSaxpy(cublasH, A.size(), &alpha, d_A, incx, d_B, incy)

　　其中alpha 是相加时的放缩系数，在文本中等于1。d_A和d_B是两个加载到device内存上的一维张量，incx和incy分别是d_A和d_B相加时的间隔距离，在本文中都等于1。

　　这样我们便实现了残差结构的并行化。

Multi-Head Attention并行化

　　对于Multi-Head Attention的并行化，本文首先根据其结构（见图5）将其分成了六个部分，分别为liner_1（计算b1=tensor*w1+b1，得到的b1（B×197×2304）为结果）、Permute_1(将b1（B×197×2304）划分得到qkv（3×B×8×197×96）)、multiplication_1(计算qk=([email protected]) ×1/sqrt(Dk))、softmax(对qk进行softmax操作)、multiplication_2(计算qk@v,将结果存到q中)以及Permute_2(将q（B×8×197×96）转化为B×197×768赋值给tensor);最后得到最终的结果。整体代码如下所示；

void MultiHeadAttention() {
    //计算b1=tensor*w1+b1，得到的b1（B×197×2304）为结果
    liner_1(768, 2304);
    //将b1（B×197*2304）划分得到qkv（3×B×8×197×96）
    Permute_1();
    //qk=([email protected])*1/sqrt(Dk)
    multiplication_1();
    //对qk进行softmax操作
    softmax();
    //计算qk@v,将结果存到q中
    multiplication_2();
    //将q（B×8×197×96）转化为B×197×768赋值给tensor
    Permute_2();
}

图5 Multi-Head Attention结构图

　　将其分成了六个部分，我们对其逐一实现并行化，其中，对于liner层以及矩阵乘法操作来说，都可以表示成下式的形式：

　　对于liner_1来说，使得上式中的α、β=1即可以实现liner层的操作，对于multiplication_1来说，我们使得α=1/sqrt(Dk)，β=0来实现这一过程，同时，在multiplication_1中B矩阵需要转置，这只需要在使用之前进行处理即可，对于multiplication_2来说，使得上式中的α=1、β=0即可以实现liner层的操作multiplication_2的操作。而在cublas中，正好提供了这样一个操作，即cublasSgemmBatched，但是需要注意的是，因为要实现的逐批次操作，因此，在调用函数之前需要进行比较复杂的操作将数据表示成二维指针的形式加载到GPU内存中，以multiplication_1为例其内存转化如下所示代码。

    /* step 2: copy data to device */
    for (int i = 0; i < m_batch_count; i++) {
        CUDA_CHECK(
            cudaMalloc(reinterpret_cast(&d_A[i]), sizeof(data_type) * Q[i].size()));
        CUDA_CHECK(
            cudaMalloc(reinterpret_cast(&d_B[i]), sizeof(data_type) * K[i].size()));
        CUDA_CHECK(
            cudaMalloc(reinterpret_cast(&d_C[i]), sizeof(data_type) * QK[i].size()));
    }

    CUDA_CHECK(
        cudaMalloc(reinterpret_cast(&d_A_array), sizeof(data_type*) * batch_count));
    CUDA_CHECK(
        cudaMalloc(reinterpret_cast(&d_B_array), sizeof(data_type*) * batch_count));
    CUDA_CHECK(
        cudaMalloc(reinterpret_cast(&d_C_array), sizeof(data_type*) * batch_count));

    for (int i = 0; i < m_batch_count; i++) {
        CUDA_CHECK(cudaMemcpyAsync(d_A[i], Q[i].data(), sizeof(data_type) * Q[i].size(),
            cudaMemcpyHostToDevice, stream));
        CUDA_CHECK(cudaMemcpyAsync(d_B[i], K[i].data(), sizeof(data_type) * K[i].size(),
            cudaMemcpyHostToDevice, stream));
        CUDA_CHECK(cudaMemcpyAsync(d_C[i], QK[i].data(), sizeof(data_type) * QK[i].size(),
            cudaMemcpyHostToDevice, stream));
    }

    CUDA_CHECK(cudaMemcpyAsync(d_A_array, d_A.data(), sizeof(data_type*) * batch_count,
        cudaMemcpyHostToDevice, stream));
    CUDA_CHECK(cudaMemcpyAsync(d_B_array, d_B.data(), sizeof(data_type*) * batch_count,
        cudaMemcpyHostToDevice, stream));
    CUDA_CHECK(cudaMemcpyAsync(d_C_array, d_C.data(), sizeof(data_type*) * batch_count,
        cudaMemcpyHostToDevice, stream));
    /* step 3: compute */
    cublasSgemmBatched(cublasH, transa, transb, m, n, k, &alpha, d_A_array, lda,
        d_B_array, ldb, &beta, d_C_array, ldc, batch_count);

    /* step 4: copy data to host */
    for (int i = 0; i < m_batch_count; i++) {
        CUDA_CHECK(cudaMemcpyAsync(QK[i].data(), d_C[i], sizeof(data_type) * QK[i].size(),
            cudaMemcpyDeviceToHost, stream));
    }

　　对于liner_1、multiplication_1、multiplication_2其对应的核函数接口如下代码所示

cublasSgemmBatched(cublasH, transa, transb, m, n, k, &alpha, d_A_array, lda,
       d_B_array, ldb, &beta, d_C_array, ldc, batch_count);

　　在具体的实现过程中，三个操作的具体参数都会有所不同，例如，以multiplication_1为例其参数如下所示。

    const int m = 197;
    const int n = 197;
    const int k = 96;
    const int lda = m;
    const int ldb = n; //k转置了
    const int ldc = m;
    const int m_batch_count = batch_count*8;

    const data_type alpha = 1 / pow(24,-0.5); //放缩系数
    const data_type beta = 0;

    data_type** d_A_array = nullptr;
    data_type** d_B_array = nullptr;
    data_type** d_C_array = nullptr;

    std::vector d_A(m_batch_count, nullptr);
    std::vector d_B(m_batch_count, nullptr);
    std::vector d_C(m_batch_count, nullptr);

    cublasOperation_t transa = CUBLAS_OP_N;
    cublasOperation_t transb = CUBLAS_OP_T; //k转置

　　然后对于softmax()和Permute，我们根据其具体的流程编写了相应的代码实现过程，这样我们便实现了Multi-Head Attention的并行化。

MLP Block并行化

　　对于MLP Block来说，其结构如图2.4所示，我们将其分成了三个部分依次并行实现，即liner_2（计算b2=tensor*w2+b2，得到的b2（B×197×3072）为结果）、GELU(对b2进行GELU操作)、liner_3（计算b3=b2*w3+b3，得到的b3（B×197×768）为结果）。最后得到最终的结果。整体代码如下所示；

void MLP() {
    //计算b2=tensor*w2+b2，得到的b2（B×197×3072）为结果
    liner_2(768,3072);
    //对b2进行GELU操作
    GELU();
    //计算b3=b2*w3+b3，得到的b3（B×197×768）为结果
    liner_3(3072,768);
    //将结果赋值给tensor
    tensor = b3;
}

　　对于liner层，我们根据之前在Multi-Head Attention中实现的方法进行实现，对于GELU来说，我们编写了gelu内核函数进行并行实现。

　　调用代码如下所示：

gelu << <608, 1024 >> > (d_A[i], b2[i].size());

　　ln内核代码如下：

__global__ void gelu(float* x, int n)
{
    int ix = threadIdx.x + blockDim.x * blockIdx.x;
    if (ix < n)
        x[ix] = 0.5 * x[ix] * (1 + tanh(sqrt(2 / 3.1415926) + 0.004715 * pow(x[ix], 3)));
        
}

　　这样我们便实现了MLP Block的并行化。

实验

实验环境

　　对于前文基于CUDA C编程根据Transformer Encoder的结构和特性对其实现并行化推理代码，我们对其性能进行测试，首先，实验的硬件环境如下表1、表2所示，软件环境如下表3所示.

表1 实验硬件环境（CPU）

型号	核心数	主频
R7-5800H	8	3.2GHz

表2 实验硬件环境（GPU）

型号	RTX 3050
计算能力	8.6
显存大小	4.96MB
CUDA Cores	2.48
GPU最大时钟频率	1.06GHz

表3 实验软件版本

CUDA	11.2
Microsoft Visual Studio	2019
PyTorch	1.10.2
Python Gcc	3.9 8.1.0

　　另外，对于实验过程中的一些参数设置，其中Batch_count=8；Input_tensor= B*197*768；在测量时间之前都会对对GPU进行充分warm up，并使用CUDA内置计时函数多次测试取平均值。

实验过程和数据

　　首先，我们根据上文中对Transformer Encoder的结构划分而得到的各个部分单独测试，并与pytorch GPU实现作比较，具体的，共有8个部分的测试，具体为LayerNorm、liner_1、multiplication_1、multiplication_2、liner_2、GELU、liner_3和Tensor_add，具体的测试结果如下表4所示。

表4 各部分运行时间测试

算子名称	CUDA C时间（ms）	pytorch时间（ms）
LayerNorm	4.65	0.1098
liner_1	0.33	1.2238
multiplication_1	0.61	0.5785
multiplication_2	0.53	0.47
liner_2	0.56	1.5905
GELU	14.75	0.99
liner_3	0.57	1.5716
Tensor_add	0.002496	0.73

　　从上表4中，我们可以看到，本文实现的算子中大部分都比pytorch GPU实现的较快，但是依然存在一些算子的并行化时间并不好，例如对于LayerNorm和GELU的实现，相比较于pytorch GPU的实现依然有很大的距离。

　　接着，本文对整个代码进行了运行测试，具体数据如下表5所示。

表5 CUDA C整体测试

完整CUDA C代码时间	202.44ms
去除GPU计算部分的完整C代码时间	180.61ms
GPU推理时间+cheek	21.83ms

表6 CUDA C和pytorch实现对比表

实现方法	时间	加速比
CUDA C	21.83ms	-
Pytorch CPU	208.62ms	9.56X
Pytorch GPU	13.30ms	0.61X

　　从上表中可以看到，本文实现的Transformer Encoder的结构并行化推理相比较于pytorch的CPU实现速度快9.56倍，相比较于pytorch的GPU实现速度快0.61倍，也就是说达到了其61%的速度，对于上述的并行化过过程中，我们也可以看到，依然存在一些不足，如表4中，LayerNorm和GELU的实现相比较于pytorch的实现都比较慢，依然存在很大的提升空间。

总结

　　本次实验为基于CUDA的Transformer Encoder并行化推理设计，本文首先根据其结构对其进行划分，将大问题转化为小问题，然后逐次编写CUDA C代码进行解决，具体的，本文首先将Transformer Encoder分为Layer Norm、Multi-Head Attention、MLP Block和残差结构四个部分，接着又对Multi-Head Attention、MLP Block进行了细分，对于Multi-Head Attention的并行化，将其分成了六个部分，分别为liner_1（计算b1=tensor*w1+b1，得到的b1（B×197×2304）为结果）、Permute_1(将b1（B×197×2304）划分得到qkv（3×B×8×197×96）)、multiplication_1(计算qk=([email protected]) ×1/sqrt(Dk))、softmax(对qk进行softmax操作)、multiplication_2(计算qk@v,将结果存到q中)以及Permute_2(将q（B×8×197×96）转化为B×197×768赋值给tensor);最后得到最终的结果。对于MLP Block来说，其结构如图2.4所示，将其分成了三个部分依次并行实现，即liner_2（计算b2=tensor*w2+b2，得到的b2（B×197×3072）为结果）、GELU(对b2进行GELU操作)、liner_3（计算b3=b2*w3+b3，得到的b3（B×197×768）为结果）。最后得到最终的结果。

　　然而，本文的实现仅仅只是使用CUDA实现了Transformer Encoder并行化推理设计，对于实现的内核函数并没有进行特定的优化，这一点有待进一步探索。

        完整版的代码受限于篇幅原因，可以通过Github获取，下面是链接：

https://github.com/zly5/OpenMP-and-PThread_Matrix-Multiplication.githttps://github.com/zly5/OpenMP-and-PThread_Matrix-Multiplication.git