代码随想录训练营第二十一天 | 530二叉搜索树的最小绝对差 501二叉搜索树中的众数 236二叉树的最近公共祖先
题目链接:530. 二叉搜索树的最小绝对差 - 力扣(Leetcode)501. 二叉搜索树中的众数 - 力扣(Leetcode)236. 二叉树的最近公共祖先 - 力扣(LeetCode)
530 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
输入:root = [4,2,6,1,3] 输出:1
自写——中序
class Solution:
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
cur_minus = 0
def _traversal(root):
nonlocal cur_minus
if not root:
return 0
self.getMinimumDifference(root.left)
minus = abs(root.val - root.left.val)
if minus > cur_minus:
cur_minus = minus
self.getMinimumDifference(root.right)
_traversal(root)
return cur_minus问题:缺少一个pre记录前一个节点;
参考代码
class Solution:
def getMinimumDifference(self, root: TreeNode) -> int:
res = []
r = float("inf")
def buildaList(root): //把二叉搜索树转换成有序数组
if not root: return None
if root.left: buildaList(root.left) //左
res.append(root.val) //中
if root.right: buildaList(root.right) //右
return res
buildaList(root)
for i in range(len(res)-1): // 统计有序数组的最小差值
r = min(abs(res[i]-res[i+1]),r)
return r501 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树
输入:root = [1,null,2,2] 输出:[2]
参考代码
class Solution:
def __init__(self):
self.pre = TreeNode()
self.count = 0
self.max_count = 0
self.result = []
def findMode(self, root: TreeNode) -> List[int]:
if not root: return None
self.search_BST(root)
return self.result
def search_BST(self, cur: TreeNode) -> None:
if not cur: return None
self.search_BST(cur.left)
# 第一个节点
if not self.pre:
self.count = 1
# 与前一个节点数值相同
elif self.pre.val == cur.val:
self.count += 1
# 与前一个节点数值不相同
else:
self.count = 1
self.pre = cur
if self.count == self.max_count:
self.result.append(cur.val)
if self.count > self.max_count:
self.max_count = self.count
self.result = [cur.val] # 清空self.result,确保result之前的的元素都失效
self.search_BST(cur.right)236 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例:
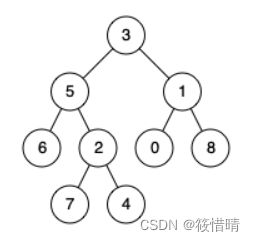
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3
后序遍历(左右中)就是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
思路:若找到一个节点,其左子树出现q/p,右子点出现p/q,那么该节点就是p和q的最近公共祖先。关键是自底向上遍历和回溯,将结果一层层向上返回直到根节点。
统共可以分为两种情况:一是p和q都在叶子节点,无论是根节点的左子树还是右子树里,如示例中p为7,q为8;二是p或q在叶子结点,另一个在其中一个根节点上,如示例中p为7,q为2。
第一种情况时,如果一个根节点的左右节点都不为空,则这个根节点就是p和q的最近公共祖先,因为他已经接受到确为p和q的左右节点的返回值了,同时具备这两个返回值的根节点就是最近公共祖先。同理,第二种情况时,如果检测到p或q为其中一个根节点,那也无需检查其子节点了。但这两个情况的前提是,已经遍历完整棵二叉树,要使用递归函数的返回值(也就是代码中的left和right)做逻辑判断。
class Solution:
"""二叉树的最近公共祖先 递归法"""
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root or root == p or root == q:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left and right:
return root
if left:
return left
return right