【数据结构】非递归实现二叉树的前 + 中 + 后 + 层序遍历(听说面试会考？)

个人主页：@Weraphael
✍作者简介：目前学习C++和算法
✈️专栏：数据结构
希望大家多多支持，咱一起进步！
如果文章对你有帮助的话
欢迎 评论 点赞 收藏 加关注✨

---

一、需要使用到的代码

1.1 二叉树的基本实现

二叉树的基本实现在以往博客已经详细讨论过了，这里直接给出本篇博客的所需用到的源代码。【数据结构】二叉树的链式结构（笔记总结）

#include 
#include 
#include 

typedef int DataType;

typedef struct BinaryTree
{
    DataType _data;
    struct BinaryTree *_left;
    struct BinaryTree *_right;
} BinaryTree;

// 创建结点
BinaryTree *CreateNode(DataType x)
{
    BinaryTree *newnode = (BinaryTree *)malloc(sizeof(BinaryTree));
    if (newnode == NULL)
    {
        printf("CreateNode failed\n");
        return NULL;
    }
    newnode->_left = NULL;
    newnode->_right = NULL;
    newnode->_data = x;

    return newnode;
}

// 建树
BinaryTree *CreateTree()
{
    // 假定树的模型如下所示
    //    1
    //  2   3
    // 4  5    6
    BinaryTree *node1 = CreateNode(1);
    BinaryTree *node2 = CreateNode(2);
    BinaryTree *node3 = CreateNode(3);
    BinaryTree *node4 = CreateNode(4);
    BinaryTree *node5 = CreateNode(5);
    BinaryTree *node6 = CreateNode(6);

    node1->_left = node2;
    node1->_right = node3;
    node2->_left = node4;
    node2->_right = node5;
    node3->_right = node6;

    return node1;
}

// 递归实现前序遍历
void PreOrder(BinaryTree *root)
{
    if (root == NULL)
        return;

    printf("%d ", root->_data);
    PreOrder(root->_left);
    PreOrder(root->_right);
}

// 递归实现中序遍历
void InOrder(BinaryTree *root)
{
    if (root == NULL)
        return;

    InOrder(root->_left);
    printf("%d ", root->_data);
    InOrder(root->_right);
}

// 递归实现后序遍历
void PostOrder(BinaryTree *root)
{
    if (root == NULL)
        return;

    PostOrder(root->_left);
    PostOrder(root->_right);
    printf("%d ", root->_data);
}

在以上源代码中，我另外给出了递归实现遍历的版本，目的是为了和非递归(迭代)版进行对比。

1.2 栈

// 需要存储的数据类型是二叉树结构体的指针！
typedef BinaryTree *DataType1;

typedef struct stack
{
    DataType1 *_a;
    int size;
    int capacity;
} stack;

void StackInit(stack *st)
{
    st->_a = (DataType1 *)malloc(sizeof(DataType1) * 4); // 假设默认大小为4
    if (st->_a == NULL)
    {
        printf("st->_a malloc failed\n");
        return;
    }
    st->capacity = 4;
    st->size = 0;
}

// 入栈
void PushStack(stack *st, DataType1 val)
{
    if (st->capacity == st->size)
    {
    	// 每次扩大两倍
        DataType1 *newcapacity = (DataType1 *)realloc(st->_a, sizeof(DataType1) * 4 * 2); 
        if (newcapacity == NULL)
        {
            printf("st->_a realloc failed\n");
            return;
        }
        st->_a = newcapacity;
        st->capacity *= 2;
    }

    st->_a[st->size] = val;
    st->size++;
}

// 判断栈是否为空
bool StackEmpty(stack *st)
{
    return st->size == 0;
}

// 出栈
void PopStack(stack *st)
{
    if (StackEmpty(st))
    {
        printf("stack is empty\n");
        return;
    }
    st->size--;
}

// 访问栈顶元素
DataType1 StackTop(stack *st)
{
     return st->_a[st->size - 1];
}

栈是后面前、中、后序遍历所需要的。但是需要注意的是：栈需要存储的数据类型是二叉树结构体的指针。为什么？在后面会详细说明。

1.3 队列

// 需要存储的数据类型是二叉树结构体的指针
typedef BinaryTree *QueueType;
typedef struct QueueNode
{
    QueueType _val;
    struct QueueNode *_next;
} QueueNode;

typedef struct Queue
{
    QueueNode *tail;
    QueueNode *head;
} Queue;

// 初始化队列
void InitQueue(Queue *q)
{
    q->tail = q->head = NULL;
}

// 插入元素
void PushQueue(Queue *q, QueueType x)
{
    QueueNode *newnode = (QueueNode *)malloc(sizeof(QueueNode));
    if (newnode == NULL)
    {
        printf("newnode create failed\n");
        return;
    }
    newnode->_next = NULL;
    newnode->_val = x;

    if (q->head == NULL)
    {
        if (q->tail != NULL)
            return;
        q->head = q->tail = newnode;
    }
    else
    {
        q->tail->_next = newnode;
        q->tail = newnode;
    }
}

// 判断队列是否为空
bool QueueEmpty(Queue *q)
{
    return (q->head == NULL) && (q->tail == NULL);
}

// 队头元素
QueueType FrontQueue(Queue *q)
{
    return q->head->_val;
}

// 出队列
void PopQueue(Queue *q)
{
    if (QueueEmpty(q))
    {
        printf("Queue is empty\n");
        return;
    }

    if (q->head->_next == NULL)
    {
        free(q->head);
        q->head = q->tail = NULL;
    }
    else
    {
        QueueNode *next = q->head->_next;
        free(q->head);
        q->head = next;
    }
}

队列是为层序遍历所准备的。同理地，队列存储的数据类型同样也要是二叉树结构体指针。

为了快速实现二叉树的遍历，以上栈和队列的细节代码并不完整。详细的可以参考往期博客：点击跳转

话不多说，现在进入正题！

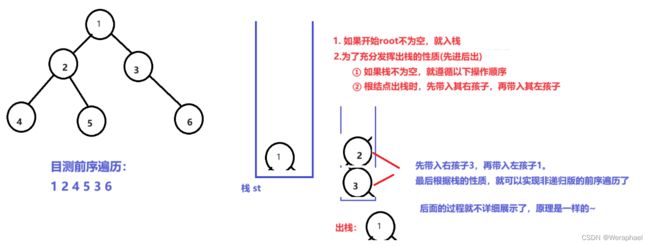
二、非递归实现二叉树的前序遍历

2.1 思路

请看下图

最后回过头来讲讲为什么栈的存储的类型要是二叉树结构体的指针？

通过上图，我们总结了：结点出栈，需要带入其左右孩子。因此，如果不是其结构体指针，那么也就无法将root的左右孩子入栈了。注意：也不能存结构体。因为一个结构体太大了，而指针的大小只有4/8字节

2.2 代码实现

// 非递归实现前序遍历
void PreOrder_nonR(BinaryTree *root)
{
	// 1. 需要一个赋值栈
    stack st;
    StackInit(&st);
	
	// 2. 如果根结点不为空入栈
    if (root != NULL)
    {
        PushStack(&st, root);
    }
    
    while (!StackEmpty(&st))
    {
    	// 记录栈顶元素
        BinaryTree *top = StackTop(&st);
		// 3. 出栈后带入其左右孩子
        PopStack(&st);
        printf("%d ", top->_data);
        // ！要注意顺序：先带右孩子，再带左孩子 
        if (top->_right)
            PushStack(&st, top->_right);

        if (top->_left)
            PushStack(&st, top->_left);
    }
}

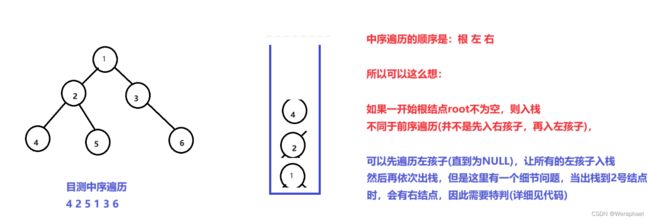
三、非递归实现二叉树的前序遍历

3.1 思路

请看下图

3.2 代码实现

void InOrder_nonR(BinaryTree *root)
{
	// 1. 需要一个辅助栈
    stack st;
    StackInit(&st);
    
    // 如果一开始根结点为NULL
    // 直接返回
    if (root == 0)
        return;

    // 2.遍历左孩子，将其全部入栈
    BinaryTree *cur = root;
    while (cur)
    {
        PushStack(&st, cur);
        cur = cur->_left;
    }

    while (!StackEmpty(&st))
    {
    	// 出栈打印
        BinaryTree *top = StackTop(&st);
        PopStack(&st);
        printf("%d ", top->_data);

        // 特判:出栈结点存在右孩子
        if (top->_right)
        {
        	// 将其入栈
            PushStack(&st, top->_right);
            // 然后还要特殊判断这个右孩子有没有左孩子
            // 因为我们要保证 先左 再根 再右
            BinaryTree *cur2 = top->_right;
            while (cur2->_left)
            {
                PushStack(&st, cur2->_left);
                cur2 = cur2->_left;
            }
        }
    }
}

四、后序遍历

4.1 思路

后序遍历我就不画图了，本人一开始写非递归后序遍历写了好久，都失败了(太菜了)。直到我看到一个视频，才知道原来后序遍历这么简单！

首先可以参考前序遍历(根左右)。因此，我们只要将前序遍历的代码逻辑的遍历顺序左和右对调一下，就变成根右左，最后再对其逆序，就是左右根，也就是后序遍历的结果了

4.2 代码实现

void PostOrder_nonR(BinaryTree *root)
{
    int res[6]; // 为了逆序
    int i = 0; // 用于遍历res数组
    memset(res, 0, sizeof(int));

    stack st;
    StackInit(&st);

    if (root != NULL)
    {
        PushStack(&st, root);
    }
    while (!StackEmpty(&st))
    {
        BinaryTree *top = StackTop(&st);
        PopStack(&st);
        res[i++] = top->_data;
		
		// 将前序遍历的代码逻辑的遍历顺序对调
        if (top->_left)
            PushStack(&st, top->_left);
        if (top->_right)
            PushStack(&st, top->_right);
    }
	// 最后逆序输出即可
    for (int k = i - 1; k >= 0; k--)
    {
        printf("%d ", res[k]);
    }
    printf("\n");
}

五、层序遍历

5.1 思路

层序遍历顾名思义就是一层一层遍历，那么就不能使用栈，得使用队列。

步骤：使用一个队列，出一个结点，带入它的孩子结点

• 如果树不为空，就先让根结点入队列
  

• 然后出队列（打印1），再把1的左孩子和右孩子带入队列
  

• 接着让2出队列，再把2的孩子入队列
  

• 同理，再让4出队列，把它的孩子入队列
  

• 最后如果队列为空，即完成层序遍历
  

5.2 代码实现

void LevelOrder(BinaryTree *root)
{
	// 1. 需要辅助队列
    Queue q;
    InitQueue(&q);
	
	// 如果一开始根结点root不为空
	// 则入队列
    if (root != NULL)
        PushQueue(&q, root);
	
	// 然后出双亲结点，带入子结点
    while (!QueueEmpty(&q))
    {
        BinaryTree *front = FrontQueue(&q);
        PopQueue(&q);

        printf("%d ", front->_data);
		
		// 带入子结点
        if (front->_left)
            PushQueue(&q, front->_left);

        if (front->_right)
            PushQueue(&q, front->_right);
    }
}

5.3 整个测试结果

六、总结

对于数据结构，还是得建议多画画图。最后我不将所有的代码整合到一块，读者只需理解，最好自己实现一遍。