线性表，栈和队列（数据结构c++）

目录

1.线性表：

2.栈

I.顺序栈

II.链栈

3.队列

I.循环队列

II.链队列

---

1.线性表：

（1）定义：

简称表，是n（n>=0）个具有相同类型的数据元素的有限序列。

（2）线性表有两种储存结构，分别是顺序储存结构——顺序表，链接储存结构——链表。

本篇文章我们着重讨论链表中的单链表。

下面代码是基于类模板的单链表的实现：

#include
using namespace std;
template        //因为不确定类型，这里我们用类模板
struct Node
{
	T data;
	Node* next;
};
template
class LinkList
{
public:
	LinkList();                  //无参构造
	LinkList(T a[], int n);      //有参构造
	~LinkList();                 //析构函数
	int Length();                //求链表长度
	T Get(int i);  //按位查找
	int Locate(T x);//按值查找
	void Insert(int i, T x);//插入操作
	T Delete(int i);
	void PrintList(); //遍历操作
private:
	Node* first;
};
template
LinkList::LinkList()
{
	first = new Node;    //生成头结点
	first->next = NULL;
}
//template
//LinkList::LinkList(T a[],int n)  //头插法
//{
//	first = new Node;    //初始化一个空链表
//	first->next = NULL;
//	for (int i = 0; i < n; i++)
//	{
//		Node* s = new Node;
//		s->data = a[i];
//		s->next = first->next;
//		first->next = s;
//	}
//}
template
LinkList::LinkList(T a[], int n)  //尾插法
{
	first = new Node;    //生成头结点
	Node* r = first;           //尾指针初始化
	for (int i = 0; i < n; i++)
	{
		Node* s = new Node;
		s->data = a[i];
		r->next = s;
		r = s;
	}
	r->next = NULL;
}
template
LinkList::~LinkList()
{
	while (first != NULL)
	{
		Node* q = first; //暂存被释放结点
		first = first->next;
		delete q;
	}
}
template
int LinkList::Length()
{
	Node* p = first->next;
	int count = 0;
	while (p != NULL)
	{
		p = p->next;
		count++;
	}
	return count;
}
template
T LinkList::Get(int i)   //按位查找
{
	Node* p = first->next;
	int count = 1;
	while (p != NULL && count < i)
	{
		p = p->next;
		count++;

	}
	if (p == NULL) throw"位置"; //抛出异常
	else
		return p->data;
}
template
int LinkList::Locate(T x)  //按值查找
{
	Node* p = first->next;
	int count = 1;
	while (p != NULL)
	{
		if (p->data == x)
			return count;
		else
		{
			p = p->next;
			count++;
		}
	}
	return 0;  //退出循环表明查找失败

}
template
void LinkList::Insert(int i, T x)  //插入操作
{
	Node* p = first;
	int count = 0;
	while (p != NULL && count < i - 1)
	{
		p = p->next;
		count++;
	}
	if (p == NULL)
		throw"位置";
	else
	{
		Node* s = new Node;
		s->data = x;
		s->next = p->next;
		p->next = s;
	}
}
template
T LinkList::Delete(int i)  //删除操作
{
	Node* p = first;
	int count = 0;
	while (p != NULL && count < i - 1)
	{
		p = p->next;
		count++;
	}
	if (p == NULL || p->next == NULL)
		throw"位置";
	else
	{
		Node* q = p->next;
		int x = q->data;     //暂存被删结点
		p->next = q->next;
		delete q;
		return x;
	}
}
template
void LinkList::PrintList()  //遍历操作
{
	Node* p = first->next;
	while (p != NULL)
	{
		cout << p->data << " ";
		p = p->next;
	}
	cout << endl;
}
void test01()
{

	int a[10];
	for (int i = 0; i < 10; i++)
		cin >> a[i];
	LinkList p(a, 10);
	cout << "按位查找第2个元素:" << p.Get(2) << endl;
	cout << "按值查找:" << p.Locate(3) << endl;
	cout << "插入操作（插入11到第二个元素的位置）" << endl;
	p.Insert(2, 11);
	p.PrintList();
	cout << "删除操作（删除第5个元素）" << endl;
	p.Delete(5);
	p.PrintList();
	cout << "链表长度为：" << endl;
	cout << p.Length();
}
int main()
{
	test01();
	return 0;
}

 输入：10 9 8 7 6 5 4 3 2 1

输出结果：

按位查找第2个元素:9
按值查找:8
插入操作（插入11到第二个元素的位置）
10 11 9 8 7 6 5 4 3 2 1
删除操作（删除第5个元素）
10 11 9 8 6 5 4 3 2 1
链表长度为：
10

2.栈

（1）栈也是线性表。

（2）定义：限定仅在表尾进行插入和删除操作的线性表，允许插入和删除的一段称为栈顶，另一端为栈底，不含任何元素的栈称为空栈。

（3）栈中的元素具有先进后出的特征。与一叠盘子类似：

 你要拿下面的盘子就需要先拿走上面的盘子。你最下面盘子是最先放的，但是要最后才能拿出来。栈也是如此，先进后出。

（4）栈的储存结构也有顺序栈和链栈。

I.顺序栈

下面代码是顺序栈的简单实现：

#include
using namespace std;
const int StackSize = 10;   //定义数组的最大长度
template
class SeqStack
{
public:
	SeqStack() { top = -1; };  //top=-1表示栈空
	~SeqStack() {};            //因为没用动态内存分配，所以析构函数为空
	void Push(T x);  //入栈
	T Pop();         //出栈
	T GetTop()       //得到栈顶元素
	{
		if (top != -1)
			return data[top];
	}
	int Empty()       //判断是否为空
	{
		if (top == -1)
			return 1;
		else
			return 0;
	}
private:
	T data[StackSize];
	int top;
};
template
void SeqStack::Push(T x)
{
	if (top == StackSize - 1)      //栈满
		throw"上溢";
	else
	{
		data[++top] = x;
	}
}
template
T SeqStack::Pop()
{
	if (top == -1)      //栈空
		throw"下溢";
	T x = data[top--];

	return x;
}
void test01()
{
	SeqStack p;
	for (int i = 0; i < 5; i++)
	{
		p.Push(i);
		cout << "入栈元素:" << i << endl;
	}
	cout << "栈顶元素为：";
	cout << p.GetTop()<

输出结果：

入栈元素:0
入栈元素:1
入栈元素:2
入栈元素:3
入栈元素:4
栈顶元素为：4
出栈操作:4 3 2 1 0

II.链栈

下面是链栈的简单实现：

#include
using namespace std;
template
struct Node
{
	T data;
	Node* next;
};
template
class LinkList
{
public:
	LinkList() { top = NULL; };
	~LinkList();
	void Push(T x);   //入栈
	T Pop();          //出栈
	T GetTop()        //得到栈顶元素
	{
		if (top != NULL)
			return top->data;
	}
	int Empty()
	{
		if (top == NULL) return 1;
		else return 0;
	}
private:
	Node* top;       //栈顶指针
};
template
LinkList::~LinkList()
{
	while (top != NULL)
	{
		Node* q = top; //暂存被释放结点
		top = top->next;
		delete q;
	}
}
template
void LinkList::Push(T x)   //入栈
{
	Node* p = new Node;
	p->data = x;
	p->next = top;
	top = p;
}
template
T LinkList::Pop()     //出栈
{
	if (top == NULL)
		throw"下溢";
	T x = top->data;
	Node* p = top;
	top = top->next;
	delete p;
	return x;
}
void test01()
{
	LinkList p;
	for (int i = 1; i <= 10; i++)
	{
		p.Push(i);
		cout << "入栈元素：" << i << endl;
	}
	cout << "栈顶元素：";
	cout << p.GetTop() << endl;
	cout << "元素出栈:";
	for (int i = 1; i <= 10; i++)
		cout << p.Pop() <<" ";
}
int main()
{
	test01();
	return 0;
}

输出结果：

入栈元素：1
入栈元素：2
入栈元素：3
入栈元素：4
入栈元素：5
入栈元素：6
入栈元素：7
入栈元素：8
入栈元素：9
入栈元素：10
栈顶元素：10
元素出栈:10 9 8 7 6 5 4 3 2 1

3.队列

(1)定义：

只允许在一端进行插入操作，在另一端进行删除操作的线性表。允许插入（也称入队，进队）的一段称为队尾，允许删除（也称出队）的一端称为队头。

（2）队列元素特征：先进先出。

就和在食堂排队一样，先来排在前面的先打饭，后来的后打饭。

 就如下图描述的一样：

 （3）队列有顺序储存结构和链接储存结构

顺序储存结构：

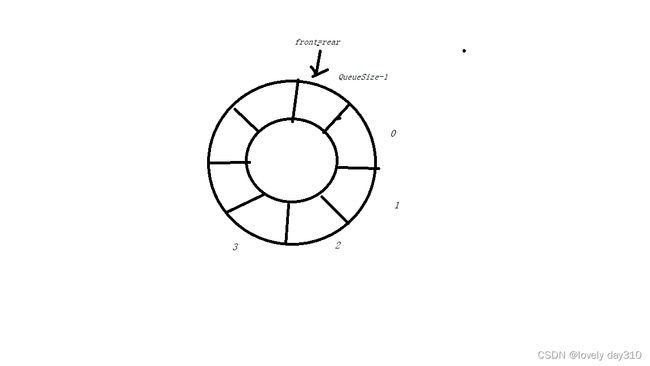
I.循环队列

这里我们讨论循环队列。如果不是循环队列那么我们队列中每个元素出对后，后面的元素都有移动一个，这样出队操作的时间开销较大。

循环队列简图如下：

 代码如下：

#include
using namespace std;
const int QueueSize = 100;
template
class CirQueue
{
public:
	CirQueue() { front = rear = QueueSize - 1; };
	~CirQueue() {};
	void EnQueue(T x);      //入队
	T DeQueue();  //出队
	T GetQueue(); //取队头元素（并不删除）
	bool isEmpty();     //判断队列是否为空
	bool isFull();      //判断队列是否满
private:
	int front, rear;
	T data[QueueSize];

};
template
void CirQueue::EnQueue(T x)   //入队
{
	if ((rear + 1) % QueueSize == front) throw"上溢";
	rear = (rear + 1) % QueueSize;
	data[rear] = x;                //在队尾插入元素
}
template
T CirQueue::DeQueue()   //出队
{
	if (rear == front) throw"下溢";
	front = (front + 1) % QueueSize;
	return data[front];
}
template
T CirQueue::GetQueue()   //取队头元素
{
	if (rear == front) throw"下溢";
	int i = (front + 1) % QueueSize;      //因为在这个代码中规定队头指针指向为空
	return data[i];
}
template
bool CirQueue::isEmpty()
{
	if (front == rear)
		return true;
	else
		return false;
}
template
bool CirQueue::isFull()
{
	if ((rear + 1) % QueueSize == front)
		return true;
	else
		return false;
}
void test01()
{
	CirQueue p;
	for (int i = 1; i <= 10; i++)
	{
		p.EnQueue(i);
		cout << "入队元素：" << i << endl;
	}
	cout << "取队头元素:";
	cout << p.GetQueue() << endl;
	cout << "出队";
	for (int i = 1; i <= 10; i++)
	{
		cout << p.DeQueue() << " ";
	}

}
int main()
{
	test01();
	return 0;
}

输出结果：

入队元素：1
入队元素：2
入队元素：3
入队元素：4
入队元素：5
入队元素：6
入队元素：7
入队元素：8
入队元素：9
入队元素：10
取队头元素:1
出队1 2 3 4 5 6 7 8 9 10 

在上述代码中数组要空一格，也就是要浪费一个数组元素空间，其中front指向空的那一格。目的是为了更好的判断队列是否为满,将队空与队满的条件分开。

队列满的条件是：（rear+1）%QueueSize=front；

队列空的条件是：rear=front；

II.链队列

代码如下：

#include
using namespace std;
template
struct Node
{
	T data;
	Node* next;
};
template
class ListQueue
{
public:
	ListQueue();
	~ListQueue();
	void EnQueue(T x);      //入队
	T DeQueue();  //出队
	T GetQueue(); //取队头元素（并不删除）
	bool isEmpty();     //判断队列是否为空
private:
	Node* front, * rear;

};
template
ListQueue::ListQueue()
{
	Node* s = new Node;
	s->next = NULL;
	front = rear = s;
}
template
ListQueue::~ListQueue()
{
	while (front->next != NULL)
	{
		Node* p = front->next;
		front->next = p->next;
		delete p;
	}
}
template
void ListQueue::EnQueue(T x)   //入队
{
	Node* s = new Node;
	s->data = x;
	s->next = NULL;
	rear->next = s;
	rear = s;

}
template
T ListQueue::DeQueue()   //出队
{
	if (rear == front) throw"下溢";
	Node* s = front->next;
	T x = s->data;
	front->next = s->next; //摘链
	if (s->next == NULL) rear = front;  //判断出队前队列长度是否为1；
	delete s;
	return x;
}
template
T ListQueue::GetQueue()   //取队头元素
{
	if (rear == front) throw"下溢";
	Node* s = front->next;
	return s->data;
}
template
bool ListQueue::isEmpty()
{
	if (front == rear)
		return true;
	else
		return false;
}
void test01()
{
	ListQueue p;
	for (int i = 1; i <= 10; i++)
	{
		p.EnQueue(i);
		cout << "入队元素：" << i << endl;
	}
	cout << "队头元素：" << p.GetQueue() << endl;
	cout << "出队:"<

输出结果：

入队元素：1
入队元素：2
入队元素：3
入队元素：4
入队元素：5
入队元素：6
入队元素：7
入队元素：8
入队元素：9
入队元素：10
队头元素：1
出队:

1 2 3 4 5 6 7 8 9 10

结语：博主也是程序小白，上述代码或语言描述肯定会存在一些问题，希望各位大佬能帮忙指出。一起进步。

如果本篇文章对您有 帮助，希望您能留下您宝贵的点赞。

参考书籍：数据结构（c++版）（第二版）（清华大学出版社）