hdu 1159 Common Subsequence
//开始DP之旅,先来道简单的
Problem Description
A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = <x1, x2, ..., xm> another sequence Z = <z1, z2, ..., zk> is a subsequence of X if there exists a strictly increasing sequence <i1, i2, ..., ik> of indices of X such that for all j = 1,2,...,k, xij = zj. For example, Z = <a, b, f, c> is a subsequence of X = <a, b, c, f, b, c> with index sequence <1, 2, 4, 6>. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.
The program input is from a text file. Each data set in the file contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct. For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.
The program input is from a text file. Each data set in the file contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct. For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.
Sample Input
abcfbc abfcab programming contest abcd mnp
Sample Output
4 2 0
Source
Recommend
/********************
求字符串 A 和 字符串 B 最长公共子序列(序列可以不连着)
用 一个二维数组 num[][] 存 当前最大的子序列长度
第一组测试数据 的num[][] 值
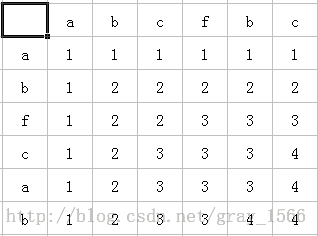
所以可以得到递推方程:
A[i] = B[j] 时,num[i][j] = num[i-1][j-1]+1;
A[i] = B[j] 时,num[i][j] = max_(num[i-1][j] , num[i][j-1]);
******************/
Code:
#include <iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
#define N 1000
int num[N][N];
int max_(int a,int b)
{
return a>b?a:b;
}
int main()
{
char A[N],B[N];
int i,j,a,b;
while(scanf("%s%s",A,B)!=EOF)
{
memset(num,0,sizeof(num));
a = strlen(A);
b = strlen(B);
for(i = 1;i<=a;i++)
{
for(j = 1;j<=b;j++)
{
if(A[i-1]==B[j-1])
num[i][j] = num[i-1][j-1]+1;
else
num[i][j] = max_(num[i-1][j],num[i][j-1]);
}
}
printf("%d\n",num[a][b]);
}
return 0;
}