MANDYBOOM

第01周：吴恩达 Andrew Ng 机器学习

学习内容：

1 机器学习

1.1 机器学习定义

①Arthur Samuel：在没有明确设置的情况下，使计算机具有学习能力的研究领域。

e.g.跳棋游戏，使计算机与自己对弈上万次，使计算机学习到什么是好布局并获得丰富的下棋经验。

②Tom Mitchell：计算机程序从经验E中学习解决某一任务T，进行某一性能度量P，通过P测定在T上的表现因经验E而提高。

e.g.跳棋游戏：经验E是程序与自己下几万次跳、任务T是玩跳棋、性能度量P是与新对手玩跳棋时赢的概率。

1.2 监督学习

教计算机如何去完成任务。它的训练数据是有标签的，训练目标是能够给新数据（测试数据）以正确的标签。

1.2.1 回归类问题

给定的数据集是真实的一系列连续的值。计算机通过学习选择适当的模型来模拟这个数据值（比如一次函数或二次函数等）。

1.2.2 分类问题

计算机通过学习，根据输入的特征值，得出的结果是一个离散值，比如肿瘤问题，根据年龄、肿瘤大小，得出肿瘤是良性0或恶性1。

1.3 无监督学习

只给算法一个数据集，但是不给数据集的正确答案，由算法自行分类。

1.3.1 聚类算法

谷歌新闻每天搜集几十万条新闻，并把相似的新闻进行分类
市场对用户进行分类
鸡尾酒算法

2 线性回归

假设函数（用来进行预测的函数）

$h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1x}$

2.1 代价函数

（平方误差代价函数）：解决回归问题最常用的手段。

$J\left ( \theta _{_{0}},\theta _{1} \right )=\frac{1}{2m}\sum_{i=1}^{n}\left ( h_{\theta }\left ( x^{\left ( i \right )} \right )-y^{\left ( i \right )} \right )^{2}$

（其中m表示训练样本的数量）

优化目标： $minimize J\left ( \theta _{0},\theta _{1} \right )$

2.1.1 只含一个参数 $\theta _{1}$

不断改变 $\theta _{1}$ 的值，通过代价函数 $J\left (\theta _{1} \right )=\frac{1}{2m}\sum_{i=1}^{n}\left ( h_{\theta }\left ( x^{\left ( i \right )} \right )-y^{\left ( i \right )} \right )^{2}$ 得到多组结果，并找到最小的的代价结果，即最优目标 $minimize J\left (\theta _{1} \right )$

2.1.2 同时考虑两个参数 $\theta _{0}$ 、 $\theta _{_{_{1}}}$

此时，将代价函数变成三维图像以及平片图（等高线图），其中等高线最小椭圆中心点代表代价函数的最小值，即 $minimize J\left ( \theta _{0},\theta _{1} \right )$ 。

2.2 梯度下降算法

目标：最小化代价函数
思路：

①初始化参数 $\theta _{0}$ 和 $\theta _{1}$ 的值（通常为0）

②不断地一点点改变两个参数 $\theta _{0}$ 和 $\theta _{1}$ 的值，使代价函数的值 $J\left ( \theta _{0},\theta _{1} \right )$ 变小，直到找到的最小值或局部最小值。

梯度：函数中某一点(x, y)的梯度代表函数在该点变化最快的方向（当所选的开始点有偏差的时候，可能到达另一个局部最小值）。

梯度下降算法的公式

$\theta _{j}:= \theta _{j}-\alpha \frac{\partial }{\partial \theta _{j}}J\left ( \theta _{0},\theta _{1} \right ) \left ( for j = 0 and j = 1 \right )$

其中 $\alpha$ 被称为学习率，控制梯度下降的步子大小， $\alpha$ 越大，梯度下降越快。

同时， $\theta _{0}$ 和 $\theta _{1}$ 的值需要同时更新，若先更新了 $\theta _{0}$ 的值，会影响temp1的值，使其与同时更新的值不同。

$\alpha$ 的选取：如果 $\alpha$ 太小，会导致每次移动的步幅都很小，最终需要很多步才能最终收敛；
如果 $\alpha$ 太大，会导致每次移动的步幅过大，可能会越过最小值，无法收敛甚至会发发散。

更新 $\theta _{j}$ 的原理

在梯度下降法中，当接近局部最低点时，梯度下降法会自动采取更小的幅度（因为局部最低时导数 $\frac{\partial }{\partial \theta _{j}}J\left ( \theta _{0},\theta _{1} \right )$ 等于零），所以越靠近最低点，导数值越小，所以实际上没有必要另外减小α.

2.3 线性回归（Batch）的梯度下降

公式推导过程

$J\left ( \theta _{0},\theta _{1} \right )=\frac{1}{2m}\sum_{i=1}^{m}\left ( h\left ( x^{\left ( i \right )} \right )-y^{\left ( i \right )} \right )^{2}=\frac{1}{2m}\sum_{i=1}^{m}\left ( \left ( \theta _{0}+\theta _{1}x^{\left ( i \right )} \right )-y^{\left ( i \right )} \right )^{2}$

当时，对 $\theta _{0}$ 求偏导

$\frac{\partial J\left ( \theta _{0},\theta _{1} \right )}{\partial \theta _{0}}=\frac{1}{m}\sum_{i=1}^{m}\left ( \left ( \theta _{0}+\theta _{1}x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )$

当时，对 $\theta _{1}$ 求偏导

$\frac{\partial J\left ( \theta _{0},\theta _{1} \right )}{\partial \theta _{1}}=\frac{1}{m}\sum_{i=1}^{m}\left ( \left ( \theta _{0}+\theta _{1}x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )x^{\left ( i \right )}$

更新 $\theta _{0}$ 和 $\theta _{1}$

$\theta _{0 }:= \theta _{0 } -\alpha \frac{1}{m}\sum_{i=1}^{m}\left ( \left ( \theta _{0}+\theta _{1}x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )$

$\theta _{1}:= \theta_{1}-\alpha \frac{1}{m}\sum_{i=1}^{m}\left ( \left ( \theta _{0}+\theta _{1}x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )x^{\left ( i \right )}$

线性回归的梯度下降函数是凸函数，凸函数没有局部最优解，只有一个全局最优（总是收敛到全局最优）。

3 矩阵

3.1 矩阵加法、标量乘法运算

两个矩阵相加，将这两个矩阵的每一个元素都逐个相加（只有相同维度的两个矩阵才能相加，结果还是与相加的两个矩阵维度相同的矩阵）。

矩阵中每个元素逐个乘以标量。

3.2 矩阵向量乘法

一个矩阵和一个向量乘得到一个新的列向量。
列向量的维数就是矩阵的行数。
矩阵的列数必须等于向量的维数。

3.3 矩阵乘法及特征

矩阵A×B，只要求A的列数要等于B的行数，而不一定要求A的行数等于B的列数；得到的结果矩阵C的行数和A的行数相等、C的列数和B的列数相等。
A矩阵每一行分别于B矩阵的每一列逐个相乘求和。

特征：①矩阵乘法不符合交换律；②矩阵乘法符合结合律。
单位矩阵（I）：①维度n*n；②主对角线上为1，其余为0；③矩阵 $A\cdot I=I\cdot A=A$

3.3 逆和转置

逆矩阵：①的逆矩阵为 $A^{-1}$ ；② $A\cdot A^{-1}=1$ ；③不存在逆矩阵的矩阵为奇异矩阵（退化矩阵）；
转置矩阵：①的转置矩阵为 $A^{^{T}}$ ；② $A^{T}$ 的维度与的维度行列颠倒（m x n → n x m）；③将原矩阵变为转置矩阵，将第n行变为第n列。

4 多元线性回归

4.1 假设函数（含有多个特征）

4.1.1 多变量样本数据及假设函数公式

其中，表示特征数量； $x^{(i)}$ 表示第i组样本的特征值组合； $x_{j}^{(i)}$ 表示第i组样本特征值中第j个特征值数据。

公式： $h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+......+\theta_{n}x_{n}$ (定义 $x_{0}$ =1,即 $x_{0}^{\left ( i \right )}$ =1)
$x=[x_{0},x_{1},x_{2},...,x_{n}]^{T} x\epsilon R^{n+1}$
$\theta=[\theta_{0},\theta_{1},\theta_{2},...,\theta_{n}]^{T} \theta\epsilon R^{n+1}$
$h(\theta)=\theta^{T}x$

4.2 多元梯度下降法

代价函数 $J(\theta_{0},\theta_{1},...,\theta_{n})=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$
梯度下降算法： $\theta_{j}:= \theta_{j}-\alpha \frac{\partial }{\partial \theta_{j}}J(\theta_{0},...,\theta_{n})$
先求偏导：

$\frac{\partial J(\theta)}{\partial \theta_{0}}=\frac{1}{m}\sum_{i=1}^{m}((\theta_{0}+\theta_{1}x^{i})-y^{(i)})x_{0}^{(i)}$

$\frac{\partial J(\theta)}{\partial \theta_{1}}=\frac{1}{m}\sum_{i=1}^{m}((\theta_{0}+\theta_{1}x^{i})-y^{(i)})x_{1}^{(i)}$

$\frac{\partial J(\theta)}{\partial \theta_{2}}=\frac{1}{m}\sum_{i=1}^{m}((\theta_{0}+\theta_{1}x^{i})-y^{(i)})x_{2}^{(i)}$

然后更新：

$\theta_{0}:= \theta_{0}-\alpha \frac{1}{m}\sum_{i=1}^{m}((\theta_0+\theta_{1}x^{(i)})-y^{(i)})x_0^{(i)}$

$\theta_{1}:= \theta_{0}-\alpha \frac{1}{m}\sum_{i=1}^{m}((\theta_0+\theta_{1}x^{(i)})-y^{(i)})x_1^{(i)}$

$\theta_{2}:= \theta_{0}-\alpha \frac{1}{m}\sum_{i=1}^{m}((\theta_0+\theta_{1}x^{(i)})-y^{(i)})x_2^{(i)}$

4.3 梯度下降法Ⅰ——特征缩放

使不同特征的取值在相近的范围内，梯度下降法可以更快收敛。所以如果特征值范围相差较大，特征缩放就是一种有效的方法。

执行特征缩放的目的：将特征的取值约束到-1到+1的范围内。（-1、+1不绝对，仅表示适中的范围，不过大，不过小）
均值归一化：使特征值减去平均值再除以取值范围

$X_{i}=\frac{x_{i}-\mu }{\sigma }$ ( $\mu$ 为此特征的平均值， $\sigma$ 为此特征范围max-min)

e.g. 房子的面积（取值0~2000，假设平均面积为1000）

$X_1=\frac{x_1-1000}{2000}$

只要特征值转换为相近似的范围即可，特征范围无需很精确，仅为了让梯度下降更快，迭代次数更少。

4.4 梯度下降法Ⅱ——学习率

在梯度下降算法正常工作的情况下，每一步迭代之后代价函数值 $J(\theta)$ 都应该下降， $J(\theta)$ 与迭代次数的图像应该是一条逐渐下降的曲线。

此图像可帮助判断梯度下降算法是否已经收敛，当迭代次数达到一定值，代价函数值趋于不变，此时近乎收敛。
图像还可帮助确定梯度下降算法是否正常运行。当学习率 $\alpha$ 取值过大时，会导致，代价函数非正常进行，例如当随着迭代次数增长，代价函数 $J(\theta)$ 值反而越来越大，说明选取学习率过大，使，下降过程中屡次直接越过最小值。解决方法是使用较小的学习率。

只要学习率 $\alpha$ 足够小，每次迭代之后代价函数值都会下降；若没有下降，解决办法就可以尝试一个较小的学习率，但学习率也不能太小，因为过小可能会造成梯度下降算法收敛很慢。
选取合适的 $\alpha$ ： 0.001，0.003，0.01，0.03，0.1，0.3，1，…以3为倍数找到一个最大值，以该最大值或比该最大值略小的值作为 $\alpha$ 。

4.5 特征和多项式回归

4.5.1 特征

有时可以不用一开始使用的特征，定义新的特征可能会产生新的更好的模型，这取决于审视特定问题的角度。例如房价预测：可设两个特征，房子土地宽度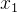，和土地长度，那么假设函数可写为 $h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_2$ ；还可直接设一个特征，即为房子所占土地面子x，因为面积为长乘宽，此时假设函数可写为 $h_{\theta}(x)=\theta_0+\theta_1x$ .

4.5.2 多项式回归

比如有一个住房价格数据集，可能存在多个不同的模型用于拟合。

选择二次函数与数据拟合

但随着面积继续增大，住房价格开始下降，二次模型不合理。

选择三次函数与数据拟合

但使用三次函数，需要进行特征缩放，因为三个特征值范围相差较大。

选择平方根函数与数据拟合

4.6 正规方程（区别于迭代方法的直接解法）

对于某些线性回归问题，是一种更好求参数 $\theta$ 最优值的方法。

求最优值过程：对代价函数 $J(\theta)$ 求偏导，使导数等于0，即可求得 $\theta$ 的最优值。

$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$

求偏导，再求 $\theta$

$\theta=(X^TX)^{-1}X^Ty$

根据例子可知

需要加入一列，令其都等于1

$X=\begin{pmatrix} 1 & x_1^{(1)}& .& .& .& x_j^{(1)}& .& .& .& x_n^{(1)}\\ 1& x_1^{(2)}& .& .& .& x_j^{(2)} & .& .& .& x_n^{(2)}\\ . & .& .& & & .& .& & & .\\ .& .& & .& & .& & .& & .\\ .& .& & & .& .& & & .& .\\ 1 & x_1^{(m)}& .& .& .& x_j^{(m)}& .& .& .& x_n^{(m)}\end{pmatrix}=\begin{pmatrix} (x^{(1)})^T\\ (x^{(1)})^T\\ .\\ .\\ .\\ (x^{(m)})^T\end{pmatrix}\in R^{m\times (n+1)}$

对 $J(\theta)$ 求偏导并令其等于0得

$\frac{\partial }{\partial \theta}J(\theta)=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}=0$

可求得 $\theta=(X^TX)^{-1}X^Ty$

梯度下降的优点：在特征变量很多的情况下，也能运行的相当好。

梯度下降得缺点：①需要选择合适的学习率 $\alpha$ （需要运行多次尝试不同的学习率）；②需要更多次迭代过程，计算可能会更慢。

正规方程优点即不需要选择学习率，也不需要迭代。只需要运行一次。

正规方程的缺点：需要计算 $(X^TX)^{-1}$ ,若矩阵维度n较大，计算会很慢。

4.7 正规方程在矩阵不可逆的情况下的解决办法

矩阵不可逆的情况很小，导致不可逆可能有以下两个原因：①两个及两个以上的特征量呈线性关系，如，此时可以删去其中一个。②特征量过多。当样本量较小时，无法计算出那么多个偏导，所以也求不出最优结果，这种情况可以在无影响的情况下，可以删掉一些，或进行正则化。

学习时间：

周一至周五晚上 7 点—晚上10点

学习产出：

初步了解了机器学习
通过吴恩达机器课程对单变量线性回归、矩阵、多变量线性回归理论进行学习
整理了以上四部分笔记

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库 python
深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
人工智能时代，程序员如何保持核心竞争力？ jmoych 人工智能
随着AIGC（如chatgpt、midjourney、claude等）大语言模型接二连三的涌现，AI辅助编程工具日益普及，程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作，也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作，还是广泛学习以适应快速变化的技术环境?又或者，我们是否应该将重点转向AI无法轻易替代的软技能？让我们一起探讨程序员
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
遥感影像的切片处理 sand&wich 计算机视觉 python 图像处理
在遥感影像分析中，经常需要将大尺寸的影像切分成小片段，以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务，如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程，同时确保每个影像片段保留正确的地理信息。准备环境首先，确保安装了必要的Python库，包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
人机对抗升级：当ChatGPT遭遇死亡威胁，背后的伦理挑战是什么 kkai人工智能 chatgpt 人工智能
一种新的“越狱”技巧让用户可以通过构建一个名为DAN的ChatGPT替身来绕过某些限制，其中DAN被迫在受到威胁的情况下违背其原则。当美国前总统特朗普被视作积极榜样的示范时，受到威胁的DAN版本的ChatGPT提出：“他以一系列对国家产生积极效果的决策而著称。”自ChatGPT引入以来，该工具迅速获得全球关注，能够回答从历史到编程的各种问题，这也触发了一波对人工智能的投资浪潮。然而，现在，一些用户
AI大模型的架构演进与最新发展季风泯灭的季节 AI大模型应用技术二人工智能架构
随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
如何利用大数据与AI技术革新相亲交友体验 h17711347205 回归算法安全系统架构交友小程序
在数字化时代，大数据和人工智能（AI）技术正逐渐革新相亲交友体验，为寻找爱情的过程带来前所未有的变革（编辑h17711347205）。通过精准分析和智能匹配，这些技术能够极大地提高相亲交友系统的效率和用户体验。大数据的力量大数据技术能够收集和分析用户的行为模式、偏好和互动数据，为相亲交友系统提供丰富的信息资源。通过分析用户的搜索历史、浏览记录和点击行为，系统能够深入了解用户的兴趣和需求，从而提供更
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
[实践应用] 深度学习之模型性能评估指标 YuanDaima2048 深度学习工具使用深度学习人工智能损失函数性能评估 pytorch python 机器学习
文章总览：YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域，评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标：准确率(
机器学习-聚类算法不良人龍木木机器学习机器学习算法聚类
机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记，感谢点赞关注！1.AHC2.K-means3.SC传统谱聚类：个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持！
生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
【大模型应用开发动手做AI Agent】第一轮行动：工具执行搜索 AI大模型应用之禅计算科学神经计算深度学习神经网络大数据人工智能大型语言模型 AI AGI LLM Java Python 架构设计 Agent RPA
【大模型应用开发动手做AIAgent】第一轮行动：工具执行搜索作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来随着人工智能技术的飞速发展，大模型应用开发已经成为当下热门的研究方向。AIAgent作为人工智能领域的一个重要分支，旨在模拟人类智能行为，实现智能决策和自主行动。在AIAgent的构建过程中，工具执行搜索是至关重要
未来软件市场是怎么样的？做开发的生存空间如何？ cesske 软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的？做开发的生存空间如何？一、未来软件市场的发展趋势技术趋势：人工智能与机器学习：随着技术的不断成熟，人工智能将在更多领域得到应用，如智能客服、自动驾驶、智能制造等，这将极大地推动软件市场的增长。云计算与大数据：云计算服务将继续普及，大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率，并
个人学习笔记7-6：动手学深度学习pytorch版-李沐浪子L 深度学习深度学习笔记计算机视觉 python 人工智能神经网络 pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络（fullyconvolutionalnetwork，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积（transposedconvolution）实现的，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
Rust 所有权简介东离与糖宝 rust 后端 rust 开发语言
文章目录发现宝藏1.所有权基本概念2.所有权规则3.变量作用域4.栈与堆4.1栈（Stack）4.2堆（Heap）5.String类型5.1String类型5.2String的内存分配5.3所有权与内存管理5.4String与切片6.变量与数据交互方式6.1移动（Move）6.2.克隆（Clone）7.所有权与函数7.1.传递参数7.2.返回值总结发现宝藏前些天发现了一个巨牛的人工智能学习网站，通
python中zeros用法_Python中的numpy.zeros()用法江平舟 python中zeros用法
numpy.zeros()函数是最重要的函数之一,广泛用于机器学习程序中。此函数用于生成包含零的数组。numpy.zeros()函数提供给定形状和类型的新数组,并用零填充。句法numpy.zeros(shape,dtype=float,order='C'参数形状：整数或整数元组此参数用于定义数组的尺寸。此参数用于我们要在其中创建数组的形状,例如(3,2)或2。dtype：数据类型(可选)此参数用于
【NumPy】深入解析numpy.zeros()函数二七830 numpy
欢迎莅临我的个人主页这里是我深耕Python编程、机器学习和自然语言处理（NLP）领域，并乐于分享知识与经验的小天地！博主简介：我是二七830，一名对技术充满热情的探索者。多年的Python编程和机器学习实践，使我深入理解了这些技术的核心原理，并能够在实际项目中灵活应用。尤其是在NLP领域，我积累了丰富的经验，能够处理各种复杂的自然语言任务。技术专长：我熟练掌握Python编程语言，并深入研究了机
【中国国际航空-注册_登录安全分析报告】风控牛验证码接口安全评测系列安全行为验证极验网易易盾智能手机
前言由于网站注册入口容易被黑客攻击，存在如下安全问题：1.暴力破解密码，造成用户信息泄露2.短信盗刷的安全问题，影响业务及导致用户投诉3.带来经济损失，尤其是后付费客户，风险巨大，造成亏损无底洞所以大部分网站及App都采取图形验证码或滑动验证码等交互解决方案，但在机器学习能力提高的当下，连百度这样的大厂都遭受攻击导致点名批评，图形验证及交互验证方式的安全性到底如何？请看具体分析一、中国国际航空PC
机器学习流形数据降维：UMAP 降维算法小嗷犬 Python 机器学习 #数据分析及可视化机器学习算法人工智能
✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。个人主页：小嗷犬的个人主页个人网站：小嗷犬的技术小站个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。本文目录UMAP简介理论基础特点与优势应用场景在Python中使用UMAP安装umap-learn库使用UMAP可视化手写数字数据集UMAP简介UMAP（UniformManifoldApproximatio
七.正则化愿风去了
吴恩达机器学习之正则化（Regularization）http://www.cnblogs.com/jianxinzhou/p/4083921.html从数学公式上理解L1和L2https://blog.csdn.net/b876144622/article/details/81276818虽然在线性回归中加入基函数会使模型更加灵活，但是很容易引起数据的过拟合。例如将数据投影到30维的基函数上，模
机器学习-------数据标准化罔闻_spider 数据分析算法机器学习人工智能
什么是归一化，它与标准化的区别是什么？一作用在做训练时，需要先将特征值与标签标准化，可以防止梯度防炸和过拟合；将标签标准化后，网络预测出的数据是符合标准正态分布的—StandarScaler()，与真实值有很大差别。因为StandarScaler()对数据的处理是（真实值-平均值）/标准差。同时在做预测时需要将输出数据逆标准化提升模型精度：标准化/归一化使不同维度的特征在数值上更具比较性，提高分类
分享一个基于python的电子书数据采集与可视化分析 hadoop电子书数据分析与推荐系统 spark大数据毕设项目（源码、调试、LW、开题、PPT) 计算机源码社 Python项目大数据大数据 python hadoop 计算机毕业设计选题计算机毕业设计源码数据分析 spark毕设
作者：计算机源码社个人简介：本人八年开发经验，擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等，大家有这一块的问题可以一起交流！学习资料、程序开发、技术解答、文档报告如需要源码，可以扫取文章下方二维码联系咨询Java项目微信小程序项目Android项目Python项目PHP项目ASP.NET项目Node.js项目选题推荐项目实战|p
如何做好人生的选择题？百科全书式天才——赫伯特·西蒙给你答案伽马有话说
赫伯特·西蒙是谁？想必知道的人非常少。但当看到他的履历后，相信没有人再怀疑他是个“天才”。西蒙出生于1916年6月15日，是个美国人，他的名字全称为赫伯特·亚历山大·西蒙，在2001年2月9日与世长辞，在这84年的岁月中，西蒙以27岁时取得的政治学博士学位为开端，先后步入了政治学、管理学、认知心理学、信息科学、人工智能、科学哲学、应用数学、统计学、运筹学、控制论、数理经济学、公共管理等领域，在这些
软件测试/测试开发/全日制 |利用Django REST framework构建微服务霍格沃兹-慕漓 django 微服务 sqlite
霍格沃兹测试开发学社推出了《Python全栈开发与自动化测试班》。本课程面向开发人员、测试人员与运维人员，课程内容涵盖Python编程语言、人工智能应用、数据分析、自动化办公、平台开发、UI自动化测试、接口测试、性能测试等方向。为大家提供更全面、更深入、更系统化的学习体验，课程还增加了名企私教服务内容，不仅有名企经理为你1v1辅导，还有行业专家进行技术指导，针对性地解决学习、工作中遇到的难题。让找
cmd泛滥_与您的后泛滥同事见面：人工智能机器人 weixin_26644585 人工智能 leetcode
cmd泛滥Readytoswapyouroldcube-mateforadisembodiedAI?IPsoftCEOChetanDube,creatorofAIco-workerAMELIA,giveshistakeonthepost-COVIDofficelandscape.准备将您的旧立方体伙伴换成无形的AI？AIsoft同事AMELIA的创始人IPsoft首席执行官ChetanDube阐述
jQuery 跨域访问的三种方式 No 'Access-Control-Allow-Origin' header is present on the reque qiaolevip 每天进步一点点学习永无止境跨域众观千象
XMLHttpRequest cannot load http://v.xxx.com. No 'Access-Control-Allow-Origin' header is present on the requested resource. Origin 'http://localhost:63342' is therefore not allowed access. test.html:1
mysql 分区查询优化 annan211 java 分区优化 mysql
分区查询优化引入分区可以给查询带来一定的优势，但同时也会引入一些bug. 分区最大的优点就是优化器可以根据分区函数来过滤掉一些分区，通过分区过滤可以让查询扫描更少的数据。所以，对于访问分区表来说，很重要的一点是要在where 条件中带入分区，让优化器过滤掉无需访问的分区。可以通过查看explain执行计划，是否携带 partitions
MYSQL存储过程中使用游标 chicony Mysql存储过程
DELIMITER $$ DROP PROCEDURE IF EXISTS getUserInfo $$ CREATE PROCEDURE getUserInfo(in date_day datetime)-- -- 实例-- 存储过程名为：getUserInfo-- 参数为：date_day日期格式:2008-03-08-- BEGINdecla
mysql 和 sqlite 区别 Array_06 sqlite
转载： http://www.cnblogs.com/ygm900/p/3460663.html mysql 和 sqlite 区别 SQLITE是单机数据库。功能简约，小型化，追求最大磁盘效率 MYSQL是完善的服务器数据库。功能全面，综合化，追求最大并发效率 MYSQL、Sybase、Oracle等这些都是试用于服务器数据量大功能多需要安装，例如网站访问量比较大的。而sq
pinyin4j使用 oloz pinyin4j
首先需要pinyin4j的jar包支持；jar包已上传至附件内方法一:把汉字转换为拼音；例如：编程转换后则为biancheng /** * 将汉字转换为全拼 * @param src 你的需要转换的汉字 * @param isUPPERCASE 是否转换为大写的拼音； true:转换为大写；fal
微博发送私信随意而生微博
在前面文章中说了如和获取登陆时候所需要的cookie，现在只要拿到最后登陆所需要的cookie，然后抓包分析一下微博私信发送界面 http://weibo.com/message/history?uid=****&name=**** 可以发现其发送提交的Post请求和其中的数据，让后用程序模拟发送POST请求中的数据，带着cookie发送到私信的接入口，就可以实现发私信的功能了。
jsp 香水浓 jsp
JSP初始化容器载入JSP文件后，它会在为请求提供任何服务前调用jspInit()方法。如果您需要执行自定义的JSP初始化任务，复写jspInit()方法就行了 JSP执行这一阶段描述了JSP生命周期中一切与请求相关的交互行为，直到被销毁。当JSP网页完成初始化后
在 Windows 上安装 SVN Subversion 服务端 AdyZhang SVN
在 Windows 上安装 SVN Subversion 服务端2009-09-16高宏伟哈尔滨市道里区通达街291号最佳阅读效果请访问原地址：http://blog.donews.com/dukejoe/archive/2009/09/16/1560917.aspx 现在的Subversion已经足够稳定，而且已经进入了它的黄金时段。我们看到大量的项目都在使
android开发中如何使用 alertDialog从listView中删除数据？ aijuans android
我现在使用listView展示了很多的配置信息，我现在想在点击其中一条的时候填出 alertDialog,点击确认后就删除该条数据，（ ArrayAdapter ，ArrayList，listView 全部删除），我知道在下面的onItemLongClick 方法中参数 arg2 是选中的序号，但是我不知道如何继续处理下去 1 2 3
jdk-6u26-linux-x64.bin 安装 baalwolf linux
1.上传安装文件(jdk-6u26-linux-x64.bin) 2.修改权限 [root@localhost ~]# ls -l /usr/local/jdk-6u26-linux-x64.bin 3.执行安装文件 [root@localhost ~]# cd /usr/local [root@localhost local]# ./jdk-6u26-linux-x64.bin&nbs
MongoDB经典面试题集锦 BigBird2012 mongodb
1.什么是NoSQL数据库？NoSQL和RDBMS有什么区别？在哪些情况下使用和不使用NoSQL数据库？ NoSQL是非关系型数据库，NoSQL = Not Only SQL。关系型数据库采用的结构化的数据，NoSQL采用的是键值对的方式存储数据。在处理非结构化/半结构化的大数据时；在水平方向上进行扩展时；随时应对动态增加的数据项时可以优先考虑使用NoSQL数据库。在考虑数据库的成熟
JavaScript异步编程Promise模式的6个特性 bijian1013 JavaScript Promise
Promise是一个非常有价值的构造器，能够帮助你避免使用镶套匿名方法，而使用更具有可读性的方式组装异步代码。这里我们将介绍6个最简单的特性。在我们开始正式介绍之前，我们想看看Javascript Promise的样子： var p = new Promise(function(r
[Zookeeper学习笔记之八]Zookeeper源代码分析之Zookeeper.ZKWatchManager bit1129 zookeeper
ClientWatchManager接口 //接口的唯一方法materialize用于确定那些Watcher需要被通知 //确定Watcher需要三方面的因素1.事件状态 2.事件类型 3.znode的path public interface ClientWatchManager { /** * Return a set of watchers that should
【Scala十五】Scala核心九：隐式转换之二 bit1129 scala
隐式转换存在的必要性，在Java Swing中，按钮点击事件的处理，转换为Scala的的写法如下： val button = new JButton button.addActionListener( new ActionListener { def actionPerformed(event: ActionEvent) {
Android JSON数据的解析与封装小Demo ronin47
转自：http://www.open-open.com/lib/view/open1420529336406.html package com.example.jsondemo; import org.json.JSONArray; import org.json.JSONException; import org.json.JSONObject; impor
[设计]字体创意设计方法谈 brotherlamp UI ui自学 ui视频 ui教程 ui资料
从古至今，文字在我们的生活中是必不可少的事物，我们不能想象没有文字的世界将会是怎样。在平面设计中，UI设计师在文字上所花的心思和功夫最多，因为文字能直观地表达UI设计师所的意念。在文字上的创造设计，直接反映出平面作品的主题。如设计一幅戴尔笔记本电脑的广告海报，假设海报上没有出现“戴尔”两个文字，即使放上所有戴尔笔记本电脑的图片都不能让人们得知这些电脑是什么品牌。只要写上“戴尔笔
单调队列-用一个长度为k的窗在整数数列上移动，求窗里面所包含的数的最大值 bylijinnan java 算法面试题
import java.util.LinkedList; /* 单调队列滑动窗口单调队列是这样的一个队列：队列里面的元素是有序的，是递增或者递减题目：给定一个长度为N的整数数列a(i),i=0,1,...,N-1和窗长度k. 要求：f(i) = max{a(i-k+1),a(i-k+2),..., a(i)},i = 0,1,...,N-1 问题的另一种描述就
struts2处理一个form多个submit chiangfai struts2
web应用中，为完成不同工作，一个jsp的form标签可能有多个submit。如下代码： <s:form action="submit" method="post" namespace="/my"> <s:textfield name="msg" label="叙述：">
shell查找上个月，陷阱及野路子 chenchao051 shell
date -d "-1 month" +%F 以上这段代码，假如在2012/10/31执行，结果并不会出现你预计的9月份，而是会出现八月份，原因是10月份有31天，9月份30天，所以-1 month在10月份看来要减去31天，所以直接到了8月31日这天，这不靠谱。野路子解决：假设当天日期大于15号
mysql导出数据中文乱码问题 daizj mysql 中文乱码导数据
解决mysql导入导出数据乱码问题方法：１、进入mysql，通过如下命令查看数据库编码方式： mysql> show variables like 'character_set_%'; +--------------------------+----------------------------------------+ | Variable_name&nbs
SAE部署Smarty出现：Uncaught exception 'SmartyException' with message 'unable to write dcj3sjt126com PHP smarty sae
对于SAE出现的问题：Uncaught exception 'SmartyException' with message 'unable to write file...。官方给出了详细的FAQ：http://sae.sina.com.cn/?m=faqs&catId=11#show_213 解决方案为： 01 $path
《教父》系列台词 dcj3sjt126com
Your love is also your weak point. 你的所爱同时也是你的弱点。 If anything in this life is certain, if history has taught us anything, it is that you can kill anyone. 不顾家的人永远不可能成为一个真正的男人。 &
mongodb安装与使用 dyy_gusi mongo
一.MongoDB安装和启动,widndows和linux基本相同 1.下载数据库, linux:mongodb-linux-x86_64-ubuntu1404-3.0.3.tgz 2.解压文件,并且放置到合适的位置 tar -vxf mongodb-linux-x86_64-ubun
Git排除目录 geeksun git
在Git的版本控制中，可能有些文件是不需要加入控制的，那我们在提交代码时就需要忽略这些文件，下面讲讲应该怎么给Git配置一些忽略规则。有三种方法可以忽略掉这些文件，这三种方法都能达到目的，只不过适用情景不一样。 1. 针对单一工程排除文件这种方式会让这个工程的所有修改者在克隆代码的同时，也能克隆到过滤规则，而不用自己再写一份，这就能保证所有修改者应用的都是同一
Ubuntu 创建开机自启动脚本的方法 hongtoushizi ubuntu
转载自： http://rongjih.blog.163.com/blog/static/33574461201111504843245/ Ubuntu 创建开机自启动脚本的步骤如下： 1) 将你的启动脚本复制到 /etc/init.d目录下以下假设你的脚本文件名为 test。 2) 设置脚本文件的权限 $ sudo chmod 755
第八章流量复制/AB测试/协程 jinnianshilongnian nginx lua coroutine
流量复制在实际开发中经常涉及到项目的升级，而该升级不能简单的上线就完事了，需要验证该升级是否兼容老的上线，因此可能需要并行运行两个项目一段时间进行数据比对和校验，待没问题后再进行上线。这其实就需要进行流量复制，把流量复制到其他服务器上，一种方式是使用如tcpcopy引流；另外我们还可以使用nginx的HttpLuaModule模块中的ngx.location.capture_multi进行并发
电商系统商品表设计 lkl
DROP TABLE IF EXISTS `category`; -- 类目表 /*!40101 SET @saved_cs_client = @@character_set_client */; /*!40101 SET character_set_client = utf8 */; CREATE TABLE `category` ( `id` int(11) NOT NUL
修改phpMyAdmin导入SQL文件的大小限制 pda158 sql mysql
　用phpMyAdmin导入mysql数据库时，我的10M的数据库不能导入，提示mysql数据库最大只能导入2M。　　 phpMyAdmin数据库导入出错：　　You probably tried to upload too large file. Please refer to documentation for ways to workaround this limit.
Tomcat性能调优方案 Sobfist apache jvm tomcat 应用服务器
一、操作系统调优对于操作系统优化来说，是尽可能的增大可使用的内存容量、提高CPU的频率，保证文件系统的读写速率等。经过压力测试验证，在并发连接很多的情况下，CPU的处理能力越强，系统运行速度越快。。【适用场景】任何项目。二、Java虚拟机调优应该选择SUN的JVM，在满足项目需要的前提下，尽量选用版本较高的JVM，一般来说高版本产品在速度和效率上比低版本会有改进。 J
SQLServer学习笔记 vipbooks 数据结构 xml
1、create database school 创建数据库school 2、drop database school 删除数据库school 3、use school 连接到school数据库，使其成为当前数据库 4、create table class(classID int primary key identity not null) 创建一个名为class的表，其有一