数据结构 第2篇--线性表学习
数据结构--线性表
- 第二章 线性表
-
- 2.1 线性表定义
- 2.2 线性表的顺序存储结构和实现(顺序表)
-
- 2.2.1 线性表的顺序存储原理
- 2.2.2 顺序存储的实现
-
- 1、创建顺序表
- 2、求顺序表容量
- 3、求顺序表长度
- 4、插入元素
- 5、删除元素
- 6、查找某个位置上的元素
- 7、清空表
- 8、销毁表
- 2.3 线性表的链式存储结构和实现(链表)
-
- 分类
-
- 单链表:
- 双向链表:
- 循环链表
- 2.3.1 链式存储的原理
- 2.3.2 链式存储的实现
-
- 1、创建链表并初始化
- 2、获取链表大小
- 3、插入元素
- 4、查找某个元素
- 5、删除元素
- 6、销毁链表
- 7、遍历打印链表
- 2.4 顺序表与链表的比较
第二章 线性表
线性表是最基础、最常用的一种线性数据结构。被广泛应用于信息存储与管理、网络、通信等诸多领域。本章将给出线性表的定义和抽象数据类型描述,讨论线性表的逻辑结构、存储结构及相关运算,并以一元整系数多项式的算术运算为实例介绍线性表的简单应用。
2.1 线性表定义
线性表是零个或多个数据元素构成的线性序列,记为(a0,a1,…,an−1)。
线性表中的数据元素个数n称为线性表的长度。
当n=0时,此线性表为空表。
线性表(a0,…,ai−1,ai,ai+1,…,an−1)中,ai表示下标为i的元素,ai−1是ai的直接前驱元素,ai+1是ai的直接后继元素。
线性表除第一个数据元素a0没有直接前驱元素,最后一个数据元素an−1没有直接后继元素之外,其他数据元素都有唯一一个直接前驱元素和直接后继元素。线性表中数据元素之间存在着一对一关系,因此,线性表的逻辑结构为线性结构。
线性表是一种非常灵活的数据结构,可在线性表的任意位置执行插入、删除元素的运算,也可执行搜索、修改等运算。
线性表是具有相同特性的数据元素组成的一个有限序列。线性表作为一种最简单的数据结构,有如下几个特征:
- 线性表中有且只有一个开始结点(头结点),这个开始节点没有前驱结点。
- 线性表中有且只有一个末尾结点(尾结点),这个末尾节点没有后继结点。
- 除去开始结点与末尾结点,其他结点都有一个前驱结点和后继结点。
线性表有两种典型的存储结构:顺序存储结构和链式存储结构,都有如下特点:
- 均匀性:虽然不同数据表的数据元素可以是各种各样的,但对于同一个线性表来说,数据元素必须具有相同的数据类型和长度。
- 有序性:各数据元素在线性表中的位置只取决于它们的序号,数据元素之间的相对位置是线性的,即**存在唯一的"第一个"和"最后一个"数据元素。除了第一个和最后一个外,其他元素前面均只有一个数据元素(直接前驱),后面均只有一个数据元素(直接后继)。
可对线性表进行的基本操作如下:
- 创建:create()
- 初始化:Init()
- 获取长度:GetLength()
- 判断表是否为空:IsEmpty()
- 获取元素:Get()
- 插入:Insert()
- 删除:Delete()
- 清空表:Clear()
2.2 线性表的顺序存储结构和实现(顺序表)
2.2.1 线性表的顺序存储原理
在存储器中分配一段连续的存储空间,逻辑上相邻的数据元素,其物理存储地址也是相邻的。
2.2.2 顺序存储的实现
1、创建顺序表
在创建顺序表时,需要先创建一个头结点来存放顺序表的长度,大小和地址等信息,然后再创建顺序表,同时将顺序表的地址保存在头结点中。
实现步骤如下:
- 定义一个struct来保存顺序表的信息
- 为头结点分配空间
- 为顺序表分配空间,将顺序表空间地址保存在头结点中
- 将头结点地址返回给调用者。
typedef struct_tag_SeqList //头结点
{
int capacity; //表容量
int length; //表长度
int *node; //node[capacity],为指针数组
}TSeqList;
//创建顺序表
SeqList* SeqList_Create(int capacity) //返回值为SeqList* 类型,即顺序表的地址
{
int ret;
TSeqList *temp = NULL;
temp=(TSeqList*)malloc(sizeof(TSeqList)); //为头结点分配空间
if(temp==NULL)
{
ret = 1;
printf("func SeqList_Create() error:%d\n",ret);
return NULL;
}
memset(temp,0,sizeof(TSeqList));
temp->capacity=capacity;
temp->lenght=0;
temp->node=(int*)malloc(sizeof(void*)*capacity); //分配一个指针数组
if(temp->node==NULL)
{
ret = 2;
printf("func SeqList_Create error %d\n",ret);
return NULL;
}
return temp; //将分配好的顺序表地址返回
}
2、求顺序表容量
在实现顺序表时,一般将顺序表信息保存在头结点中,因此求顺序表容量时,可以直接从头结点中获取。
int SeqList_Capacity(SeqList* list)
{
TSeqList *temp = NULL;
if(list == NULL)
{
return;
}
temp=(TSeqList *)list;
return temp->capacity;
}
3、求顺序表长度
//求顺序表长度
int SeqList_Length(SeqList* list)
{
TSeqList *temp = NULL;
if(list == NULL)
{
return;
}
temp = (TSeqList*)list;
return temp->length;
}
4、插入元素
在线性表中插入元素时,元素和元素后面的元素都要后移。在插入过程中,需要考虑异常情况:
- 当顺序表已满时,表中的元素无法向后移动,需要作出特别处理(例如不插入,或者申请新开辟一块更大的空间来存储这些元素)
- 当插入的位置在空闲区域时,需要作出相应处理。
//插入元素
int SeqList_Insert(SeqList* list,SeqListNode *node,int pos)
//参数为顺序表地址,要插入的元素地址,插入位置
{
int i;
TSeqList *temp = NULL;
//先做健壮性检查
if(list == NULL || node == NULL)
{
return -1;
}
temp=(TSeqList *)list;
//如果顺序表已满
if(temp->length>=temp->capacity)
{
return -2;
}
//容错
if(pos>temp->length)
pos=temp->length;
for(i=temp->length;i>pos;i--)
{
temp->node[i]=temp->node[i-1];
}
temp->node[i]=(int)node;
temp->length++;
return 0;
}
5、删除元素
从顺序表中删除某一个元素,则将某一个元素删除后,需要将后面的元素依次向前移动来补齐空位
//删除元素
SeqList* SeqList_Delete(SeqList* list,int pos)
{
int i;
//先做健壮性检查
TSeqList* tlist = NULL;
SeqListNode * temp = NULL;
tlist = (TSeqList *)list;
if(list==NULL||pos<0||pos>=tlist->capacity)
{
printf("SeqList_Delete() error%d\n");
return NULL
}
temp=(SeqListNode*)tlist->node[pos]; //要删除的元素
for(i=pos+1;i<tlist->length;i++)
{
tlist->node[i-1]=tlist->node[i];
}
tlist->length--;
return temp;
}
6、查找某个位置上的元素
//查找某个位置上的元素
SeqList* SeqList_Get(SeqList * list,int pos)
{
int i;
TSeqList* tlist = NULL;
SeqListNode* temp = NULL;
tlist = (TSeqList*)list;
if(list=NULL||pos<0||pos>tlist->capacity)
{
return NULL;
}
temp = (SeqListNode*)tlist->node[pos];
return temp;
}
7、清空表
清空顺序表是将表中的内容全部置为0
//清空顺序表
void SeqList_Clear(SeqList*list)
{
TSeqList*temp = NULL;
if(list==NULL)
{
return;
}
temp=(TSeqList*)list;
temp->length=0;
memset(temp->node,0,(temp->capacity * sizeof(void*)));
return;
}
8、销毁表
销毁表是将表整个销毁,无法再使用
//销毁表
void SeqList_Destroy(SeqList* list)
{
TSeqList* temp = NULL;
if(list == NULL)
{
return;
}
temp = (TSeqList*)list;
if(temp->node!=NULL)
{
free(temp->node);
}
free(temp);
return;
}
2.3 线性表的链式存储结构和实现(链表)
线性表的顺序存储结构着明显的缺点:插入、删除元素时需要频繁移动元素,运算效率低;必须按事先估计的最大元素个数申请连续的存储空间。存储空间估计大了,则浪费空间;若估计小了,则容易产生溢出,空间难以临时扩大。采用链式存储结构的线性表可以克服线性表的顺序存储结构存在的上述不足。
采用链式存储结构的线性表称为链表。链表有单链表、循环链表和双向链表等多种类型。
分类
单链表:
指的是链表中的元素的指向只能指向链表中的下一个元素或者为空,元素之间不能相互指向,也就是一种线性链表
是否带头节点分成两种
typedef int DataType;
typedef struct Node{
DataType data;
struct node *next;
} ListNode;
双向链表:
一个有序的结点序列,每个链表元素既有指向下一个元素的指针,又有指向前一个元素的指针,其中每个结点都有两种指针,即front和tail,front指针指向左边结点,tail指针指向右边结点

typedef int DataType;
typedef struct DNode{
DataType data;
struct node *front;
struct node *tail;
} DListNode;
循环链表
指的是在单向链表和双向链表的基础上,将两种链表的最后一个结点指向第一个结点从而实现循环
2.3.1 链式存储的原理
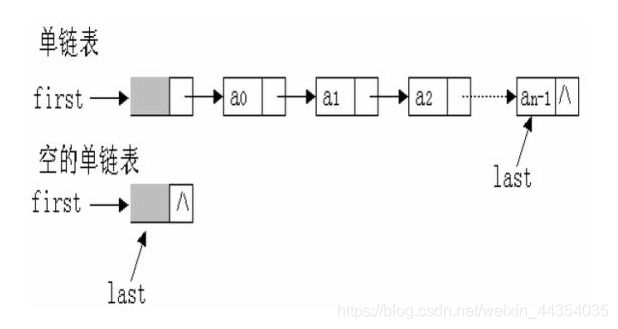
链表都有一个头指针,一般以head来表示,存放的是一个地址。链表中的节点分为两类,头结点和一般节点,头结点是没有数据域的。链表中每个节点都分为两部分,一个数据域,一个是指针域。
每个结点只包含一个指针域的链表,称为单链表。
2.3.2 链式存储的实现
1、创建链表并初始化
typedef是C语言的关键字,作用是为一种数据类型定义一个新名字。使用typedef的目的一般有两个,一个是给变量一个易记且意义明确的新名字,另一个是简化一些比较复杂的类型声明。
struct Header //头结点
{
int length; //纪录链表大小
struct Node* next; //指向第一个节点的指针
}
struct Node //结点
{
int data; //记录结点数据
struct Node* next; //指向下一个节点的指针
}
typedef struct Node List; //将Node重命名为List
typedef struct Header pHead; //将Header重命名为pHead
//链表初始化
pHead* createList()
{
pHead* ph =(pHead*)malloc(sizeof(pHead));
ph->length = 0;
ph->next = NULL;
return ph;
}
2、获取链表大小
int Size(pHead* ph)
{
if(ph==Null)
{
printf("参数传入有误");
return 0 ;
}
return ph->length;
}
3、插入元素
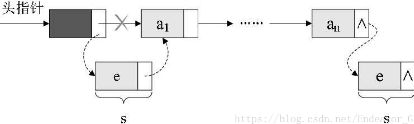
插入节点就是用插入前节点的指针域链接上插入节点的数据域,再把插入节点的指针域链接上插入后节点的数据域。
int Insert(pHead* ph,int pos,int val)
{
//先做健壮性检查
if(ph==NULL||pos<0||pos>ph->length)
{
printf("参数传入有误");
return 0;
}
//在向链表中插入这个元素时,先找到这个元素
List* pval=(List*)malloc(sizeof(List)); //先分配一块内存来存储要插入的数据
pval->data=val;
List *pCur = ph->next; //当前指针指向头结点的第一个节点
if(pos==0)
{
ph->next=pval;
pval->next=pCur;
}
else
{
for(int i=1;i<pos;i++)
{
pCur=pCur->next;
}
pval->next=pCur->next;
pCur->next=pval;
}
ph->length++;
return 1;
}
4、查找某个元素
查找链表中的某个元素,其效率没有顺序表高,因为不管查找的元素在哪个位置,都需要将前面的元素都全部遍历才能找到它。
List* find(pHead*ph,int val)
{
//先做健壮性检查
if(ph == NULL)
{
printf("输入的参数有误");
return NULL;
}
List *pTmp = ph->next;
do{
if(pTmp->data==val)
{
return pTmp;
}
pTmp=pTmp->next;
}while(pTmp->next!=NULL);
printf("没有值为%d的元素",val);
return NULL;
}
5、删除元素
在删除元素时,首先将被删除元素与上下节点之间的连接断开,然后将这两个上下节点重新连接,这样元素就从链表中成功删除了。
List* Delete(pHead*ph,int val)
{
//先做健壮性检查
if(ph == NULL)
{
printf("链表为空,删除失败");
return NULL;
}
//找到val值所在的节点
List* pval=find(ph,val);
if(pval == NULL)
{
printf("没有值为%d的元素",val);
return NULL;
}
//遍历链表找到要删除的节点,并找出其前驱及后继结点
List *pRe = ph->next; //当前节点
List *pCur = ph->NULL;
if(pRe->data == pval)
{
ph->next=pRe->next;
ph->length--;
return pRe;
}
else
{
for(int i=0;i<ph->length;i++)
{
pCur=pRe->next;
if(pCur->data == pval)
{
pRe->next = pCur->next;
ph->length--;
return pCur;
}
pRe = pRe->next;
}
}
}
6、销毁链表
void Destory(pHead *ph)
{
List *pCur=ph->next;
list *pTmp;
if(ph==NULL)
printf("参数传入有误");
while(pCur->next!=NULL)
{
pTmp = pCur->next;
free(pCur);
pCur=pTmp;
}
ph->length=0;
ph->next=NULL;
}
7、遍历打印链表
void print(pHead *ph)
{
if(ph==NULL){
printf("打印不了,这个链表是空的");
}
List *pTmp=ph->next;
while(pTmp !=NULL)
{
printf("%d",p->data);
pTmp = pTmp->next;
}
printf("\n");
}
2.4 顺序表与链表的比较
以上介绍了线性表的两种存储结构:顺序表和链表。顺序表和链表各有其优缺点,不能笼统地说哪种存储结构更好,只能根据实际问题的具体需要,并对各方面的优缺点加以综合分析比较,才能选择出符合应用需求的存储结构。以下从时间性能和空间性能两方面对顺序表和链表进行比较。
1.时间性能方面
顺序表是随机存取结构,完成按位置随机访问的运算的时间复杂度为O(1);链表不具有随机访问的特点,按位置访问元素时只能从表头开始依次遍历链表,直至找到特定的位置,平均时间复杂度为O(n)。
对于链表,在确定插入或删除的位置后,只需修改指针即可完成插入或删除运算,所需的时间复杂度为O(1);顺序表进行插入或删除操作时,需移动近乎表长一半的元素,平均时间复杂度为O(n)。尤其是当线性表中元素个数较多时,移动元素的时间开销相当可观。
如上所述,若线性表需频繁进行插入和删除操作,则宜采用链表做存储结构。若线性表需频繁查找却很少进行插入和删除操作或其所做运算和“数据元素在线性表中的位置”密切相关,则宜采用顺序表作为存储结构。
2.空间性能方面
顺序表需要预分配一定长度的存储空间,若存储空间预分配过大,将导致存储空间浪费;若存储空间预分配过小,将造成空间溢出问题。链表不需要预
存储空间浪费;若存储空间预分配过小,将造成空间溢出问题。链表不需要预分配空间,只要有可用的内存空间分配,链表中的元素个数就没有限制。
综上所述,当线性表中元素个数变化较大或者未知时,应尽量采用链表作为存储结构;当线性表中元素个数变化不大,可事先确定线性表的大致长度时,可采用顺序表作为存储结构。
也可参考该博客线性表的相关介绍