VelvetShiki_Not_VS

链表OJ——逆序链表，移除链表元素问题

文章目录

✨逆置链表
- - 逆序链表指向法
  - 头插法
✨链表移除元素
- - 跳过val值结点法
  - 非val值结点尾插法
⭐后话

✨逆置链表

剑指 Offer II 024. 反转链表 - 力扣（LeetCode）

描述：给一个头结点head，反转该链表

即head = 1,2,3,4,5，反转后head = 5,4,3,2,1

思路：

头插原结点，用newhead和cur记录原结点和记录新节点地址。

让原有节点指向空，后继结点反指前一结点，通过三个指针pre, cur, next指针备份地址和指向地址

逆序链表指向法

逆序单链表的一种思路是，定义三个指针分别指向待掉转指向的目标结点和其前后结点，需要三个指针的原因是为了备份目标结点和前后结点地址，防止丢失某个结点的地址：

如果只定义指向一个结点的指针，则该结点只能通过链表结构next指向其后继结点地址，而无法逆指向其前一个结点，如存在链表

1->2->3->NULL

3无法指向2,2也无法指向1,1可以后继置空，但独立称为了仅有1->NULL的新链表
如果只定义两个指针，一个指向遍历链表的当前结点cur，一个指向其前一个结点pre，如果不创建一个临时的结构体指针保存当前结点的后继结点地址，当当前结点逆指向前一个结点的地址时，其后继结点的地址也会丢失：

1->2->3->4->5->NULL

其中pre指向当前结点前一结点，cur指向当前结点，比如此时pre指向1，cur指向2

则使用cur->next = pre，pre->next = NULL，达成了逆置效果，有2->1->NULL

但是当cur想继续向后遍历寻找结点值为3的结点时，因为cur->next已经该指向1，所以3的地址丢失了
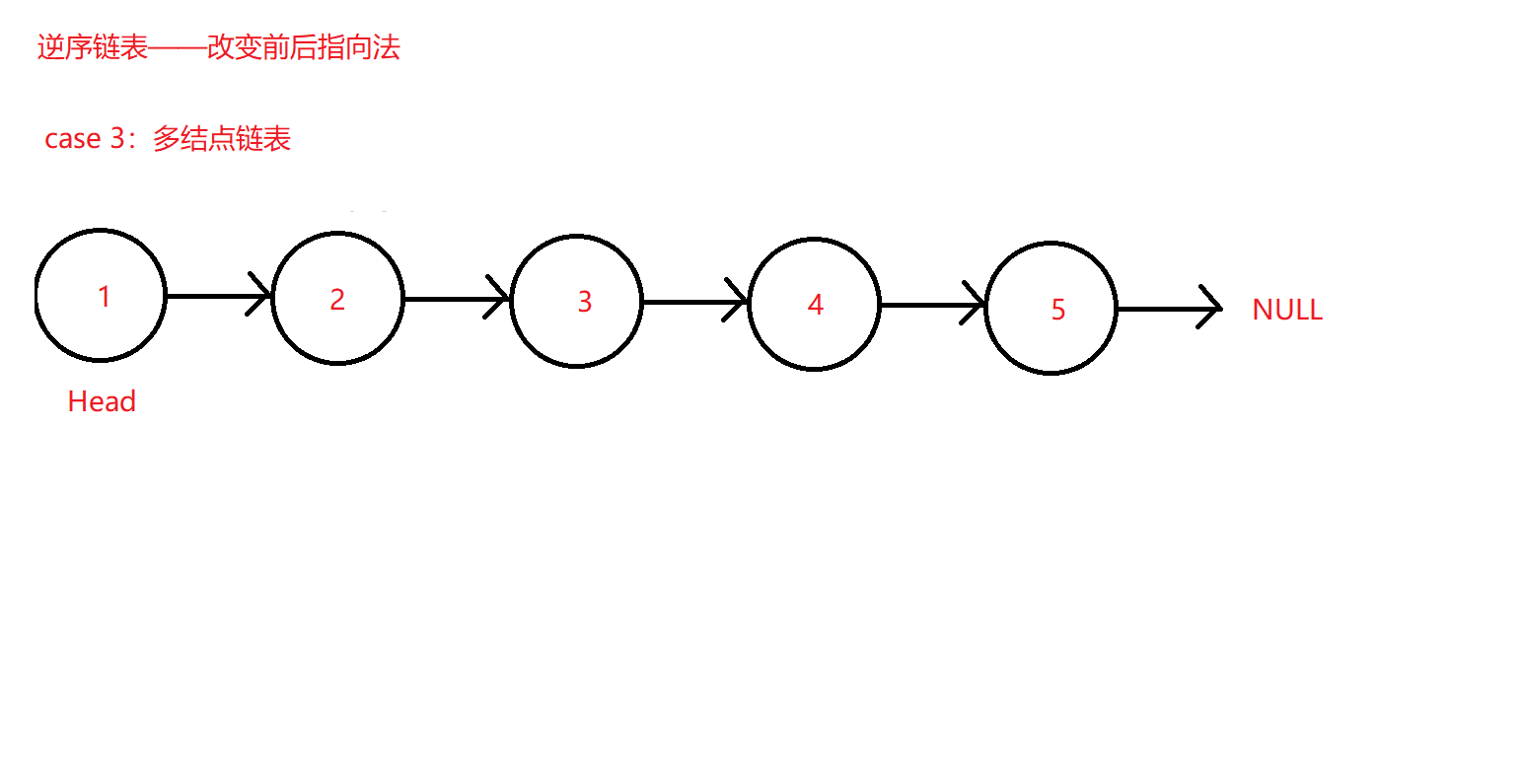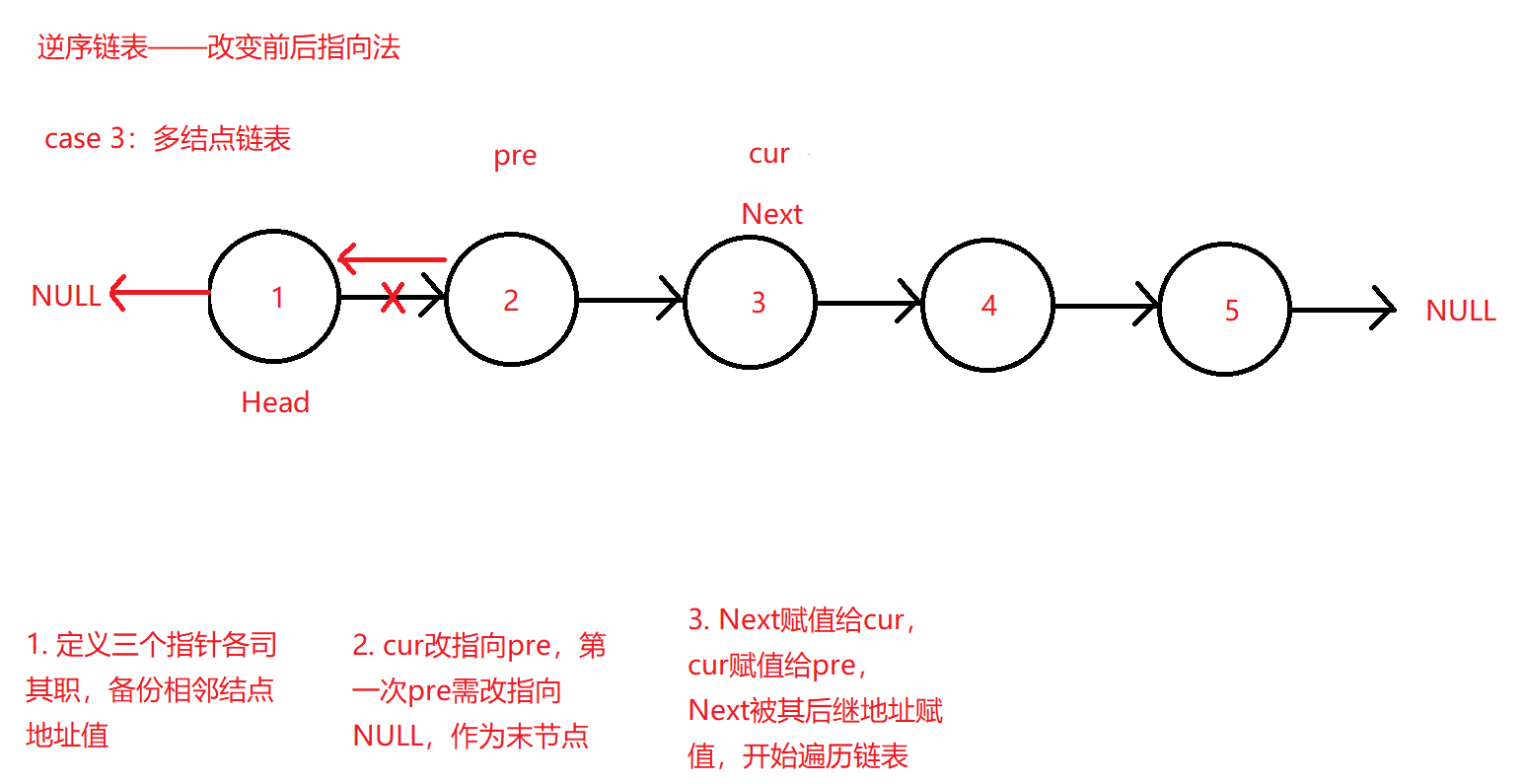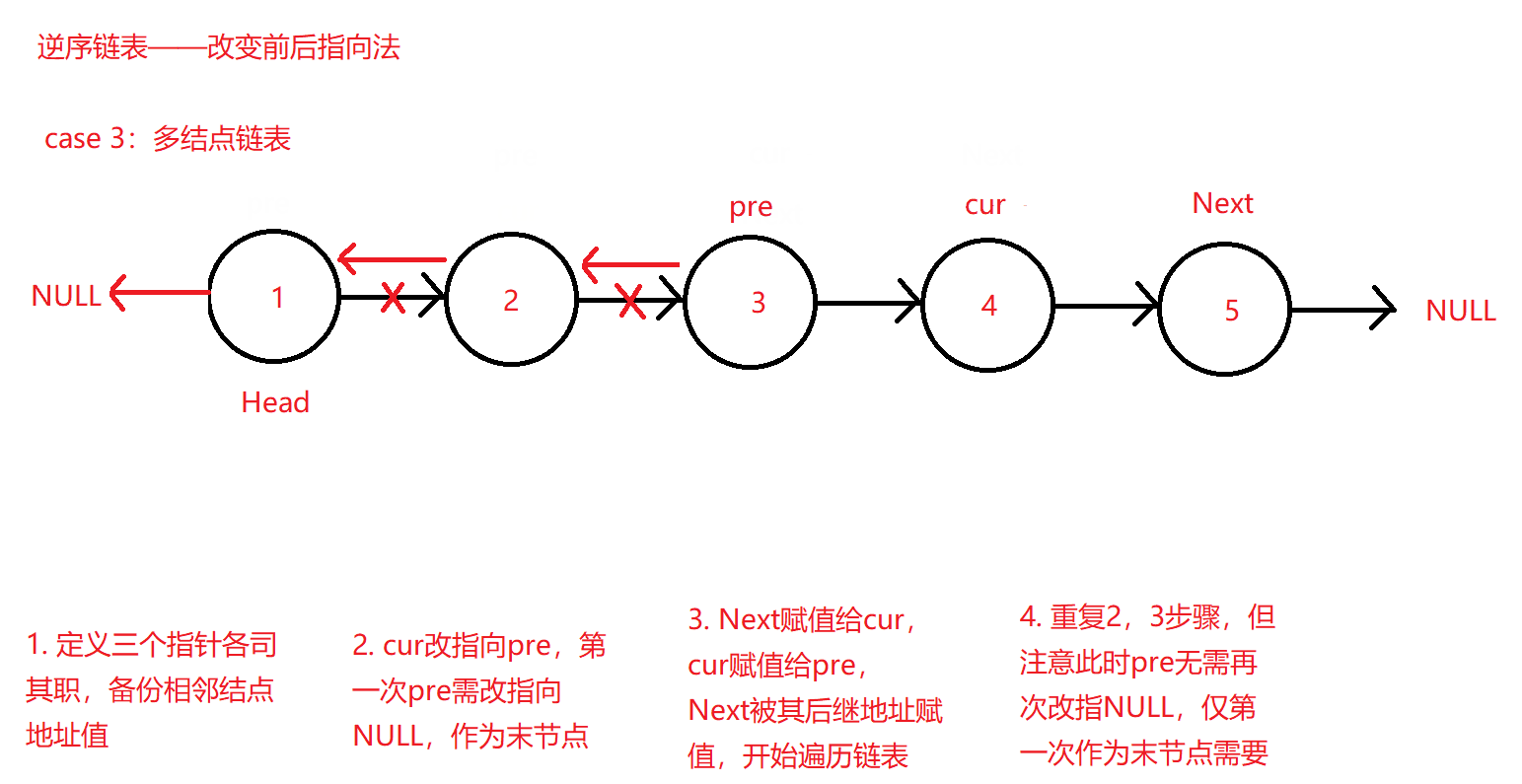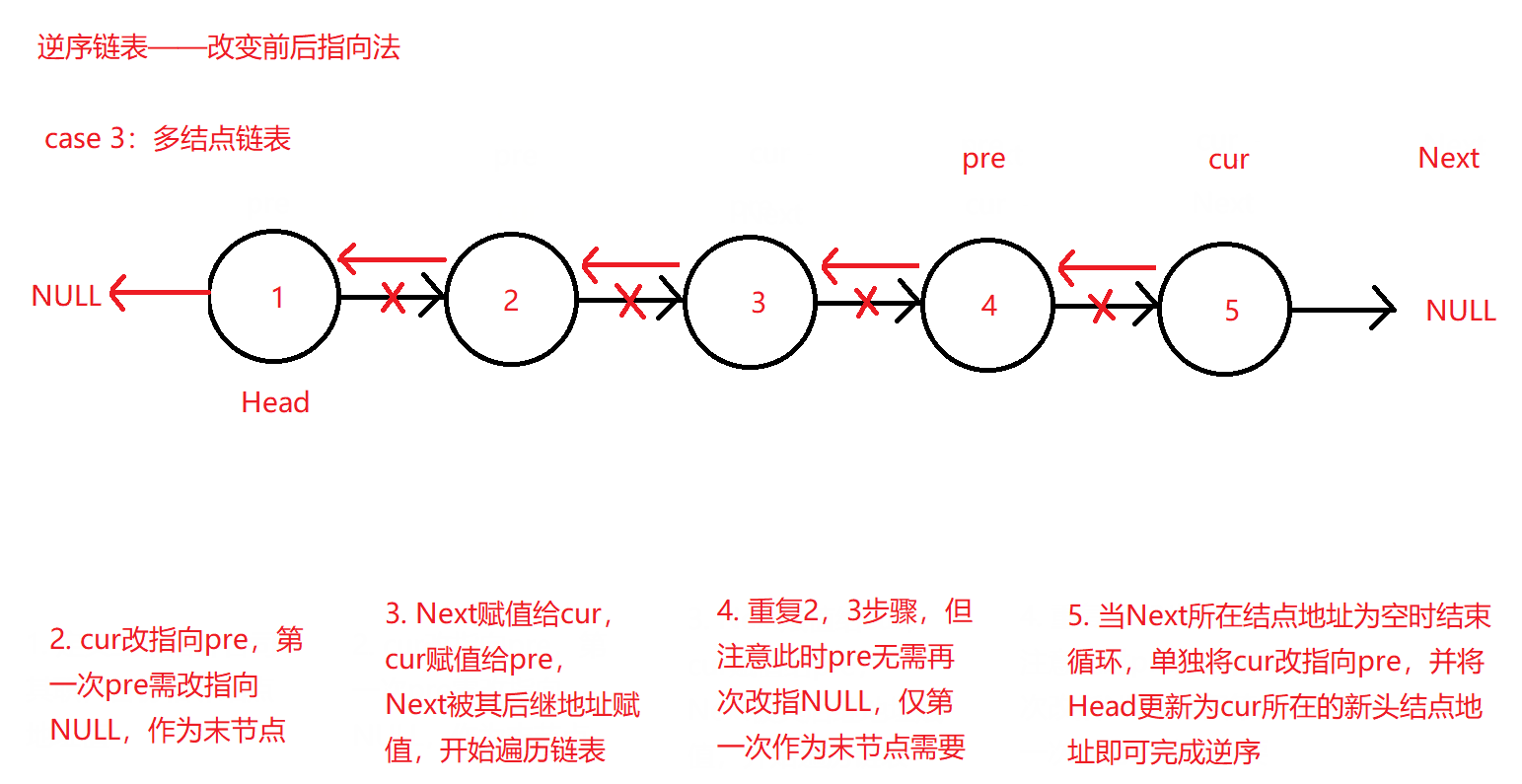
所以定义三个指针：

pre指向当前结点前一结点地址

cur指向当前结点地址

Next指向当前结点的下一结点地址

可以解决前两个用例中前后结点地址丢失的问题，因为都分别被单独的指针将与当前结点相邻的结点地址都备份起来了，所以无论当前结点的后继如何指向，都不会造成链表遍历找不着北，无法继续循环的问题。

三指针逆序算法

SgL* ReverseSL(SgL* Head)					//逆置链表算法
{	
	assert(Head);							//暴力判空法，如果链表没有任何结点，则报错
	SgL* pre = Head;
	SgL* cur = Head->next;
	if (Head->next == NULL)					//判断是否为单结点链表
	{
		return Head;
	}
	if (Head->next->next == NULL)			//判断是否为双结点链表
	{
		cur->next = pre;
		pre->next = NULL;
		return cur;
	}
	else
	{	
		SgL* Next = Head->next->next; 		//三个指针pre, cur, Next分别存储前中后结点，并改变指向循环到Next == NULL
		int count = 1;
		while(Next)
		{
			cur->next = pre;
			if (count == 1)
			{
				pre->next = NULL;			//将新尾结点后继置空
				count--;
			}
			pre = cur;
			cur = Next;
			Next = Next->next;
		}
	}
	cur->next = pre;
	return cur;
}

说明：

观察函数传参，仅仅传入了链表头结点地址的一级指针，如果按照基本链表函数接口的做法都是传入二级指针，因为可能存在头结点地址对实参更新或删除等问题，但此处因为存在返回值，所以即使传入一级指针也可以通过返回值将更新后的头结点地址返回给实参，如果不使用返回值的做法就必须通过二级指针传参以修改链表实参值了。
函数开头采用了断言法直接判断此链表是否为空，该方法较为简单暴力，因为如果对没有任何结点的链表执行逆序算法是没有意义的。
先定义当前结点指针cur和前一结点指针pre，用于对结点较少的链表进行逆序操作。初始化需将pre指针以头结点Head地址赋值，而当前指针则从第二个结点地址开始向后遍历。此时需要注意，如果传入的链表仅有一个结点，则cur的值目前就为NULL，如果事先定义好指向当前结点的下一结点的指针Next就会造成非法访问，即产生了NULL->next，这就是函数开始对于非空链表只能定义两个指针的原因。
对于仅有一个结点的链表，无论怎么指向，其后继都是NULL所以不需要多余处理。而对于两个结点的链表，直接将cur所在的第二结点的后继指向pre所在的头结点地址，再将头结点后继置空，返回cur作为新的头结点地址即可完成小于三个结点的链表逆序操作。
而对于存在多个（大于或等于3个）结点的链表而言，后继指针Next就需要定义并派上用场了。pre初始化为链表头结点地址，cur为第二个结点地址，而Next为cur的下一结点的地址，即第三个结点地址。
后续链表逆序的操作大体上和仅有两个结点的后继改指向操作基本一致，只不过多了一个后继备份指针Next用于给cur赋值继续遍历链表，cur指向pre后又让cur的地址值赋值给pre，这样两两赋值和改指向就可以让cur不仅可以正常遍历链表到末节点，且可以不断改变其指向到pre完成逆序操作了。

原理图如下：
当链表采用此方法逆序完成后，需要注意，原来的末节点将成为需要返回的新的逆序链表头结点地址给实参，从而使实参通过该函数接收到新的链表头结点值，而原头结点便成为了当前逆序链表的末节点并指向空NULL。

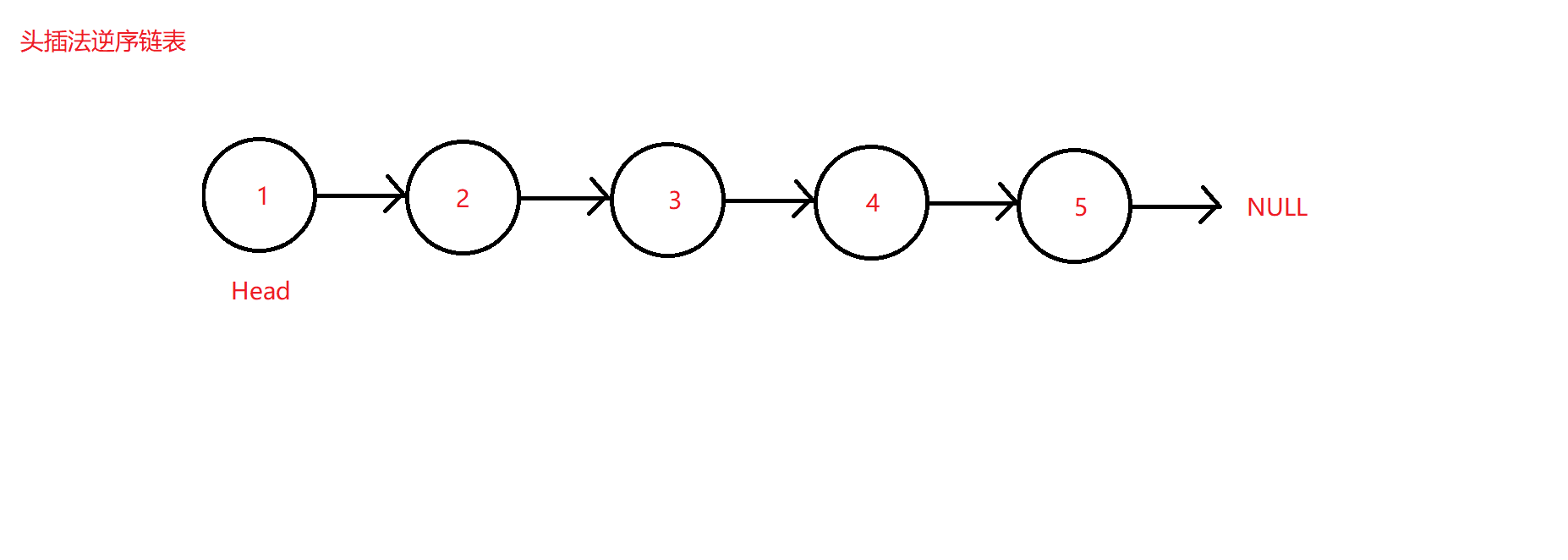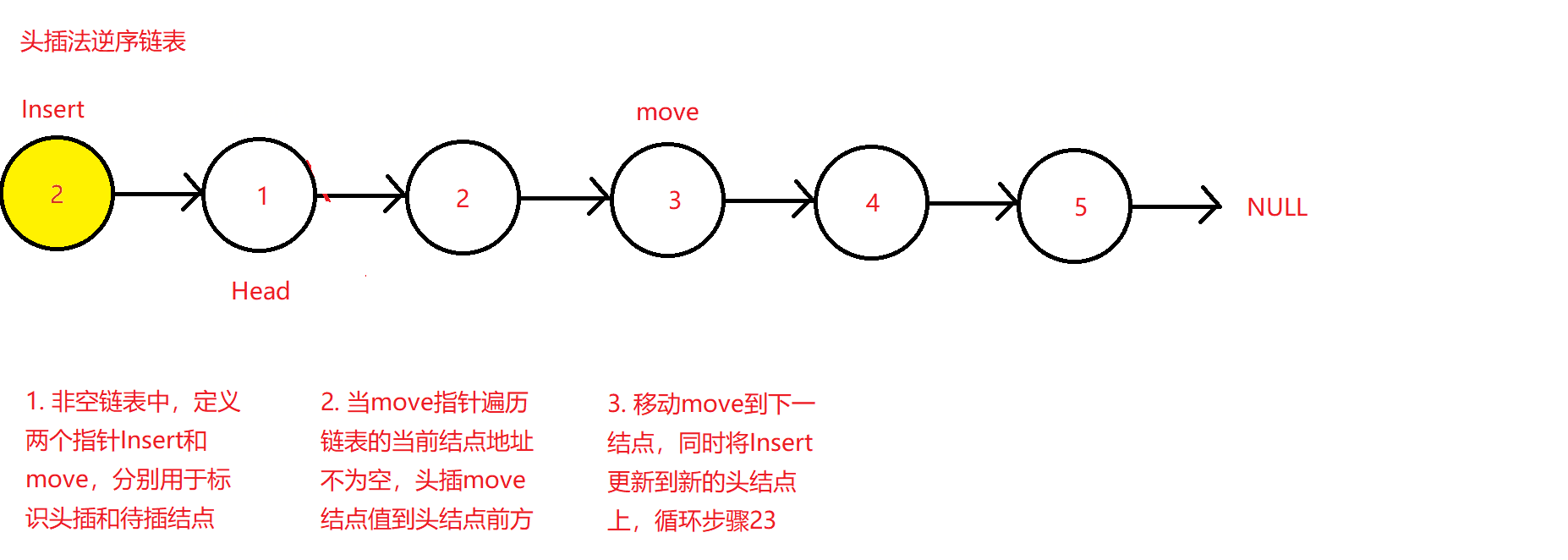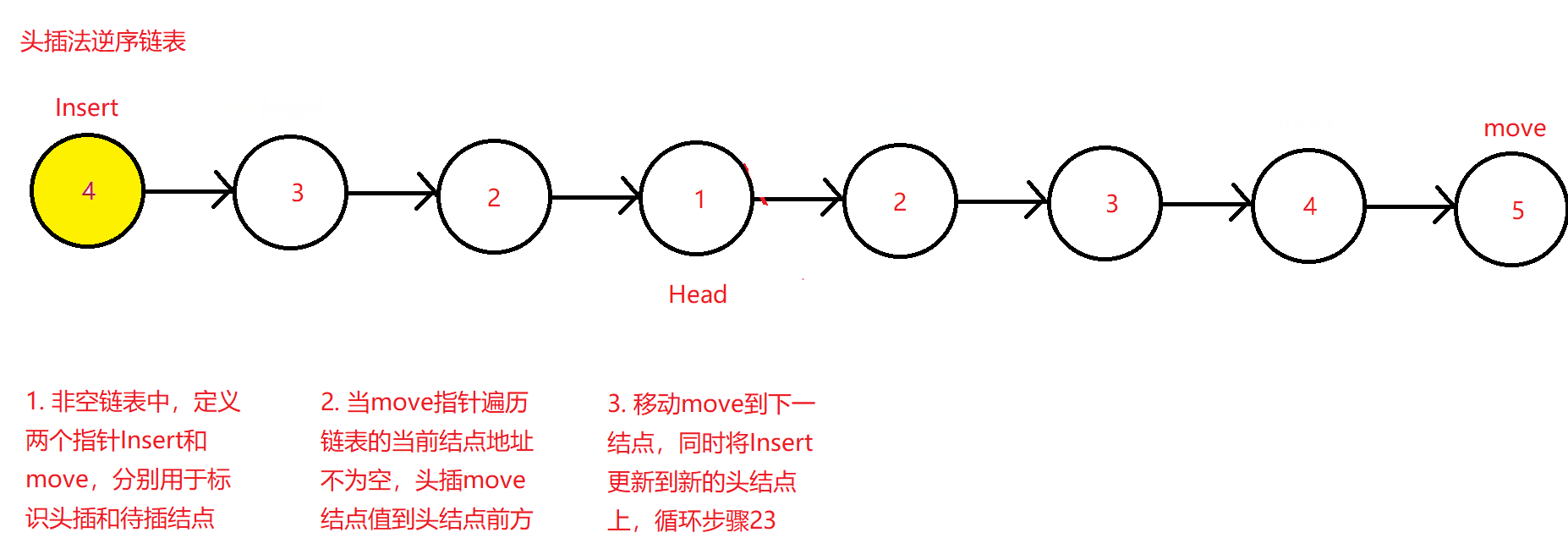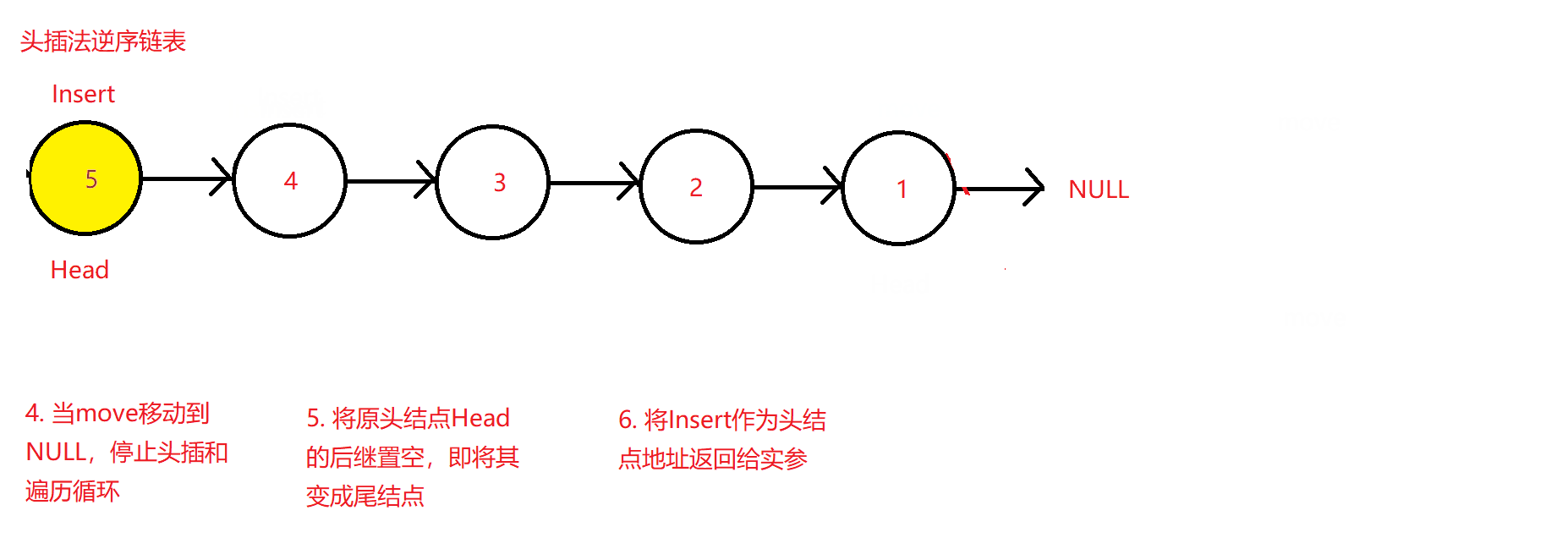
头插法

对比上述需要定义三个指针的方法和对单结点链表，双结点链表和多结点链表需要进行单独的判断，可以采用另外一种更简洁的方法。其大体思路为将除头结点外的后续连接的结点依次头插到原头结点的前方，比如1->2->3->4，将2头插到1前，并更新头结点到2处，再将3头插到头结点2之前，完成后又让3成为新的头结点，以便后续的4头插到3之前，按照这样的思路在函数内部循环调用直至原头结点1之后的所有结点全部完成头插，最终的效果是让原来的末节点成为新逆序链表的头结点，而原头结点则成为了新链表的末节点，其后继指针指向空值。

头插逆序算法

SgL* ReverseSL2(SgL* Head)					//逆置链表算法
{
	if (Head == NULL)
	{
		return NULL;
	}
	SgL* move = Head->next;					//定义一个结点指针遍历原链表,初始时默认移动到原链表第二个结点处，等待头插
	SgL* Insert = Head;						//定义一个新链表结点指针，用于头插指向
	while (move)
	{
		Insert = PushFront(Insert, move->data);			//将move指向结点头插入insert结点
		move = move->next;
	}
	Head->next = NULL;						//将原来的头结点后续指针置空
	return Insert;
}

其中头插函数

SgL* PushFront(SgL* Head, Etype x)							//头插函数
{
	assert(Head);
	SgL* NewHead = BuyListNode(x);
	NewHead->next = Head;
	return NewHead;
}

观察函数，传入的参数为实参代表的链表头结点地址，但此处没有采用断言，而是对传入的结点地址进行if判断监测，如果传入了一个无任何结点的链表地址，则返回NULL，为除开断言报错的另一种不执行函数但也不报错的返回措施。
在此逆序函数中，定义了两个指向且可应用于任何非空链表的结点指针move和Insert，前者用于标识待头插的结点和遍历链表，后者用于标识被头插的结点并使其成为新的头结点。即两个指针起到了一个表示结点待插入，一个表示结点已经头插入。

原理图如下：

测试用例——输入如下具有7个结点的链表并调用逆序函数观察结果

//定义和开辟结点
SgL* n1 = BuyListNode(1);
SgL* n2 = BuyListNode(2);
SgL* n3 = BuyListNode(3);
SgL* n4 = BuyListNode(4);
SgL* n5 = BuyListNode(5);
SgL* n6 = BuyListNode(6);
SgL* n7 = BuyListNode(7);
//链接各个结点
n1->next = n2;
n2->next = n3;
n3->next = n4;
n4->next = n5;
n5->next = n6;
n6->next = n7;
printf("原链表结构为：");
Print(n1);
//调用并返回逆序后的头结点地址
SgL* NewHead = ReverseSL(n1);
printf("逆序后链表结构为：");
//打印链表
Print(NewHead);

观察结果

原链表结构为：1->2->3->4->5->6->7->NULL
逆序后链表结构为：7->6->5->4->3->2->1->NULL

如果传入一个空链表，则直接返回NULL，而不会像第一种方法使用断言assert判断那样直接报错并指明判空报错的具体代码行数，两种方法各有优缺点，可以根据代码需求酌情考虑使用。

✨链表移除元素

链表中将指定元素擦除在之前链表的结构定义和基本函数接口已经有过大致了解，最直观和简单的一种思路就是通过Find函数将需要擦除的值对应的结点先找出来，再对该结点执行Erase删除操作并链接前后结点成为新链表即可。但是这样的方法需要不断循环并遍历链表，其时间复杂度为O(N²)，如果链表数据量过大则可能造成运算时间过长。除了这种基本思路以外，这里还提供了另外两种解题思路以供参考。

跳过val值结点法

如果将待擦除的结点数值域定义为val，当一个结点指针指向该结点并对比val和数值域数据，如果相等就将该结点的前一个结点的后继指针next改指向到待擦除结点的后继结点，具体的操作方法为定义两个指针pre和cur，都以头结点地址赋值，让cur指针遍历链表，遇到cur->data与val值相等就备份该结点后继地址，释放cur所在结点并移动cur到后继结点，如果后继结点不为val则让pre也移动到该结点上。

第一种情况是链表中存在一个或多个不连续的val结点等待删除，这些结点有可能出现在头部，也有可能出现在链表中间或尾部。如果val结点位于头部，则直接执行头删操作并让新的头结点地址重新赋值pre和cur即可。

以如下4个结点的链表为例：
可以看出，在执行头删前，pre和cur指针就事先移动到了Head的后继，此时如果是单结点链表，头结点后继为空，则直接结束循环，返回一个没有任何结点的空链表，表示需要删除的结点都删除干净了。
如果后续还有结点存在且该结点不为val，则仅移动cur指针向后遍历链表，后续再出现val结点则使用tmp备份其后继结点，释放cur所在的val结点后移动到已经备份好的tmp结点处，如果该结点不为val或空，才移动pre指针到cur结点处，此后cur继续遍历，并重复上述步骤。
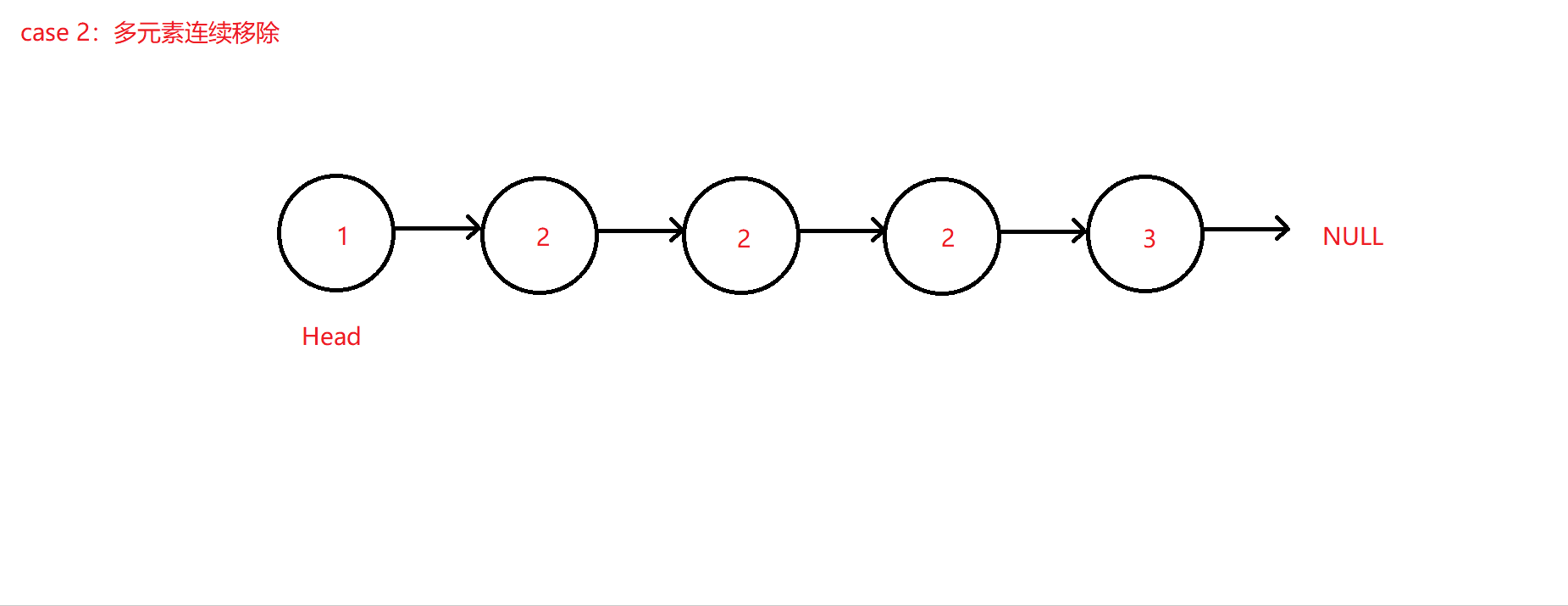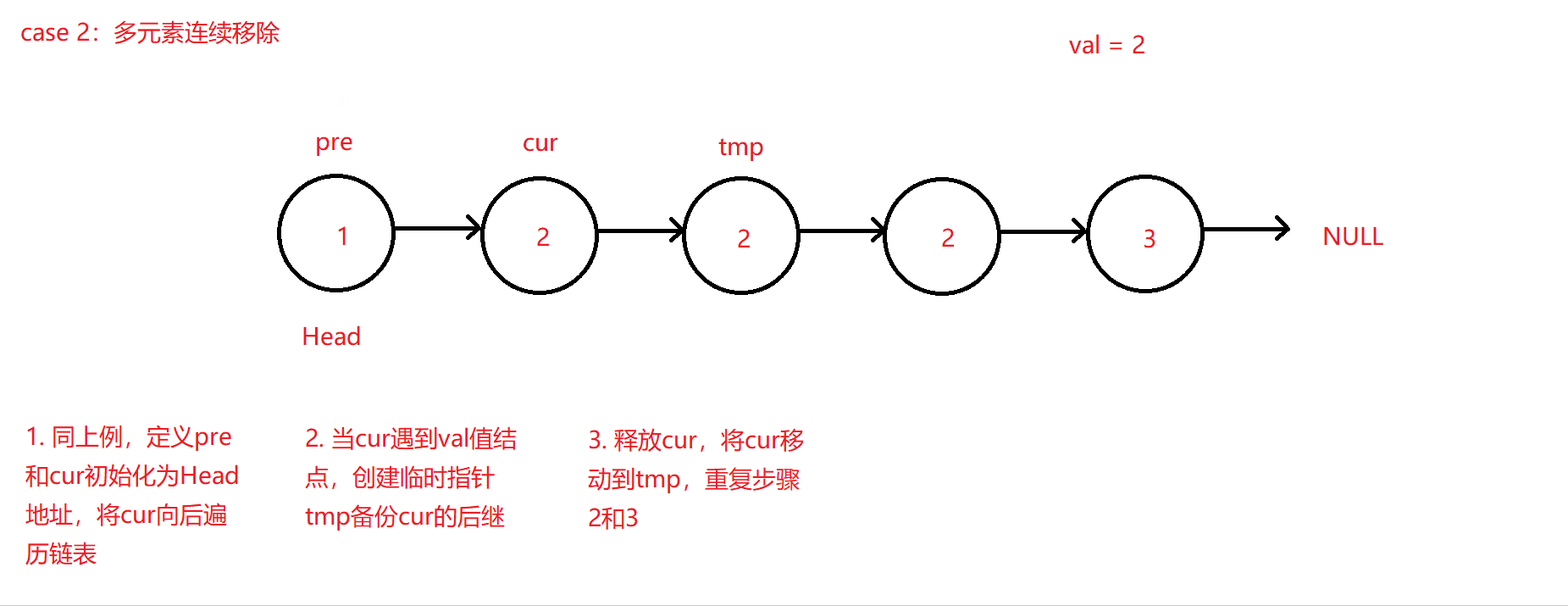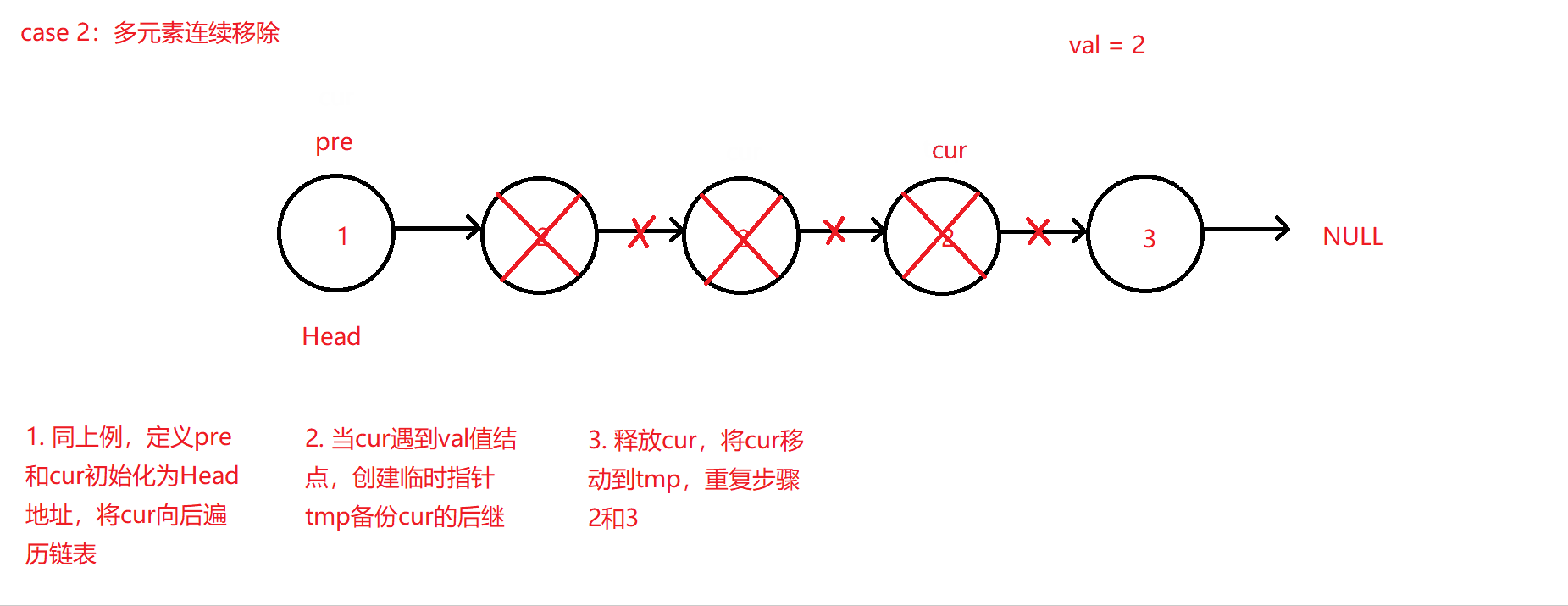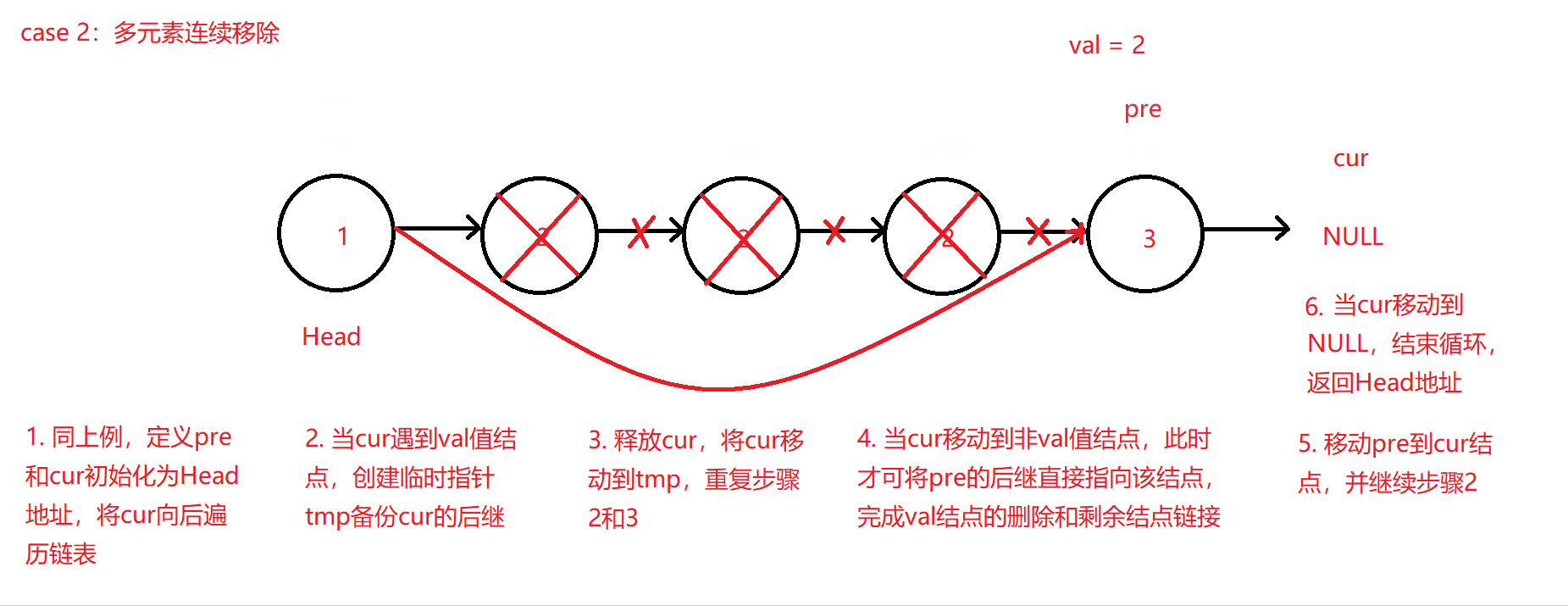
如果多个连续的结点都为val值，则连续移动cur和创建的临时指针tmp来不断释放结点和后移，仅当cur后移所处结点不为val值或空值NULL，此时才可将pre指针赋值更新到cur所在结点地址，原理大体同上。因为该算法代码考虑情况较为复杂且定义的指针相对较多，所以此处不进行代码赘述，可移步至码云查看链表移除元素算法VelvetShiki_Not_VS/C_Practice - 码云。

非val值结点尾插法

同样需要定义两个指针Insert和move，但与前例的用于标识带链接改指向结点不同，move指针用于遍历原链表寻找非val结点，Insert指针用于将move找到的非val值结点尾插到一个新的链表中，且该新链表中的所有结点必不包含原链表中带有val值的结点。

非val尾插移除元素算法

SgL* PushBack_not_Val(SgL* Head, Etype val)
{
	if (Head == NULL)
	{
		return NULL;
	}
	SgL* NewHead = NULL, *Insert = NULL;
	SgL* move = Head;
	bool flag = true;
	while (move)
	{
		if (move->data != val && flag)			//第一个非val结点作为新链表首节点
		{
			NewHead = BuyListNode(move->data);
			Insert = NewHead;
			flag = false;
		}
		else if (move->data != val)				//后续非val结点作为新首节点后续的插入结点
		{
			Insert = PushBack(Insert, move->data);
			Insert = Insert->next;
		}
		move = move->next;						//若进入循环，每次循环移动move结点指针遍历链表
	}
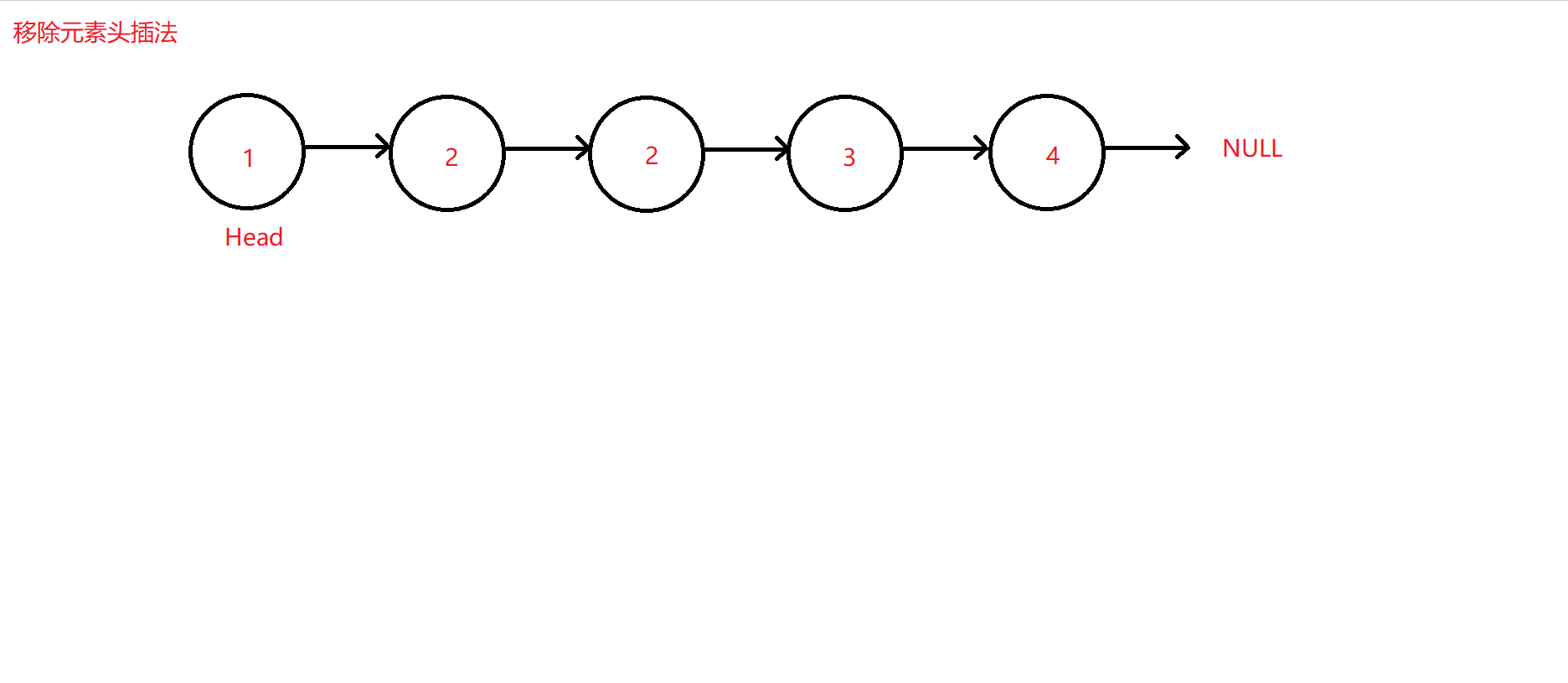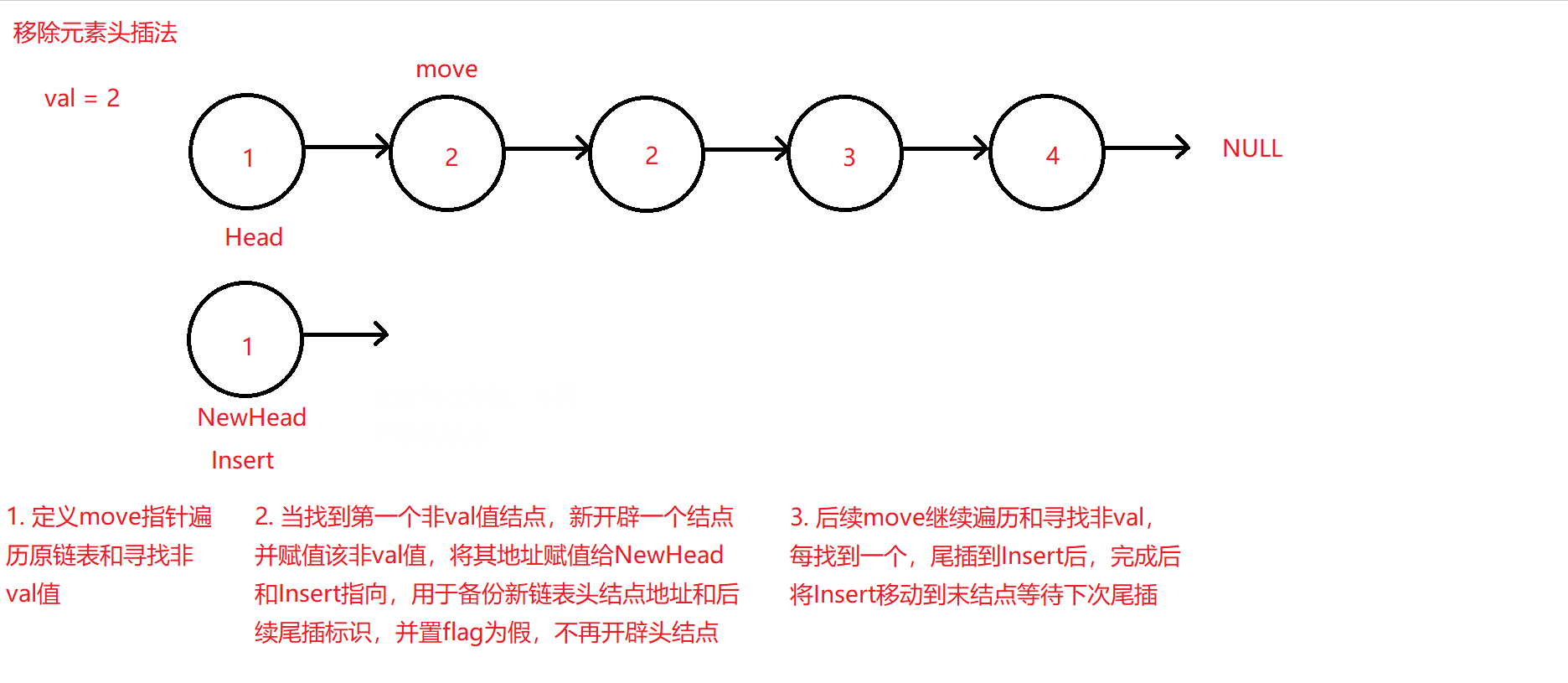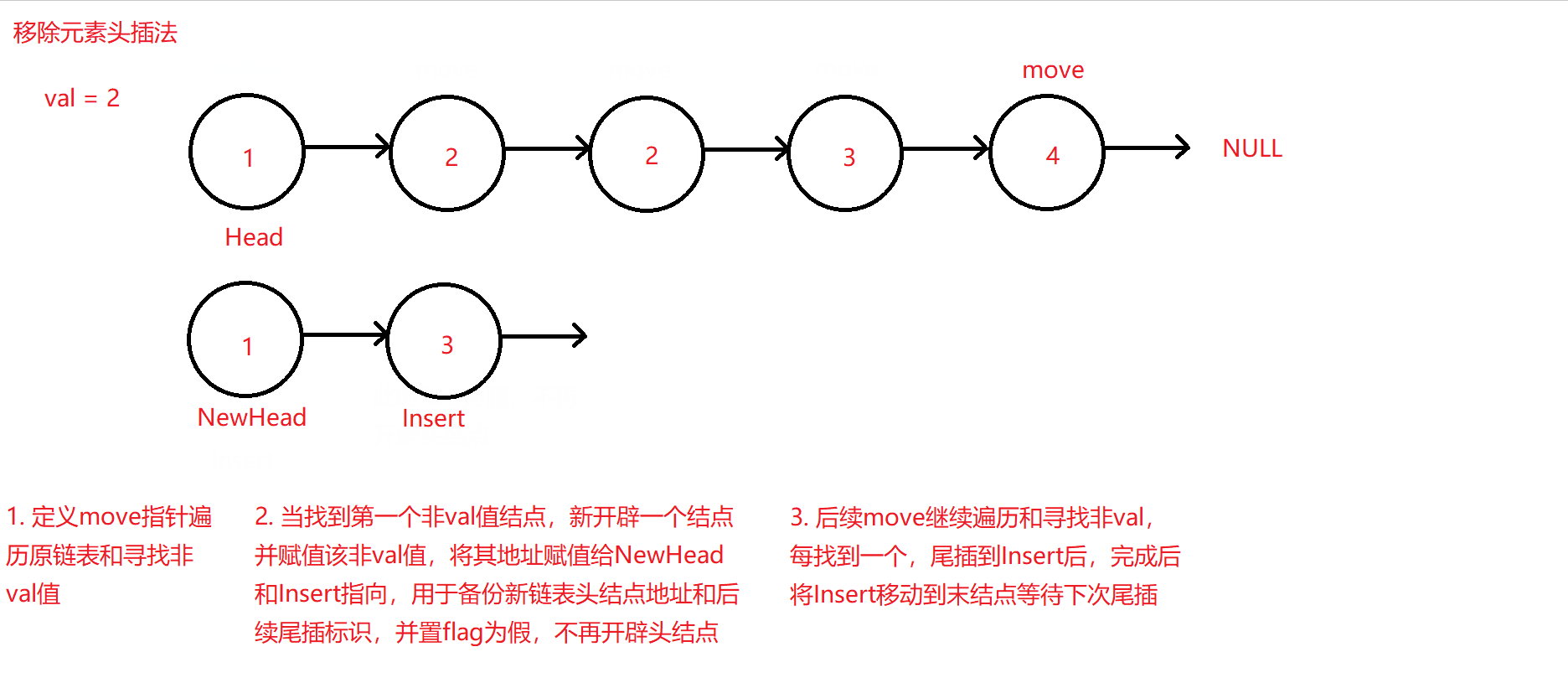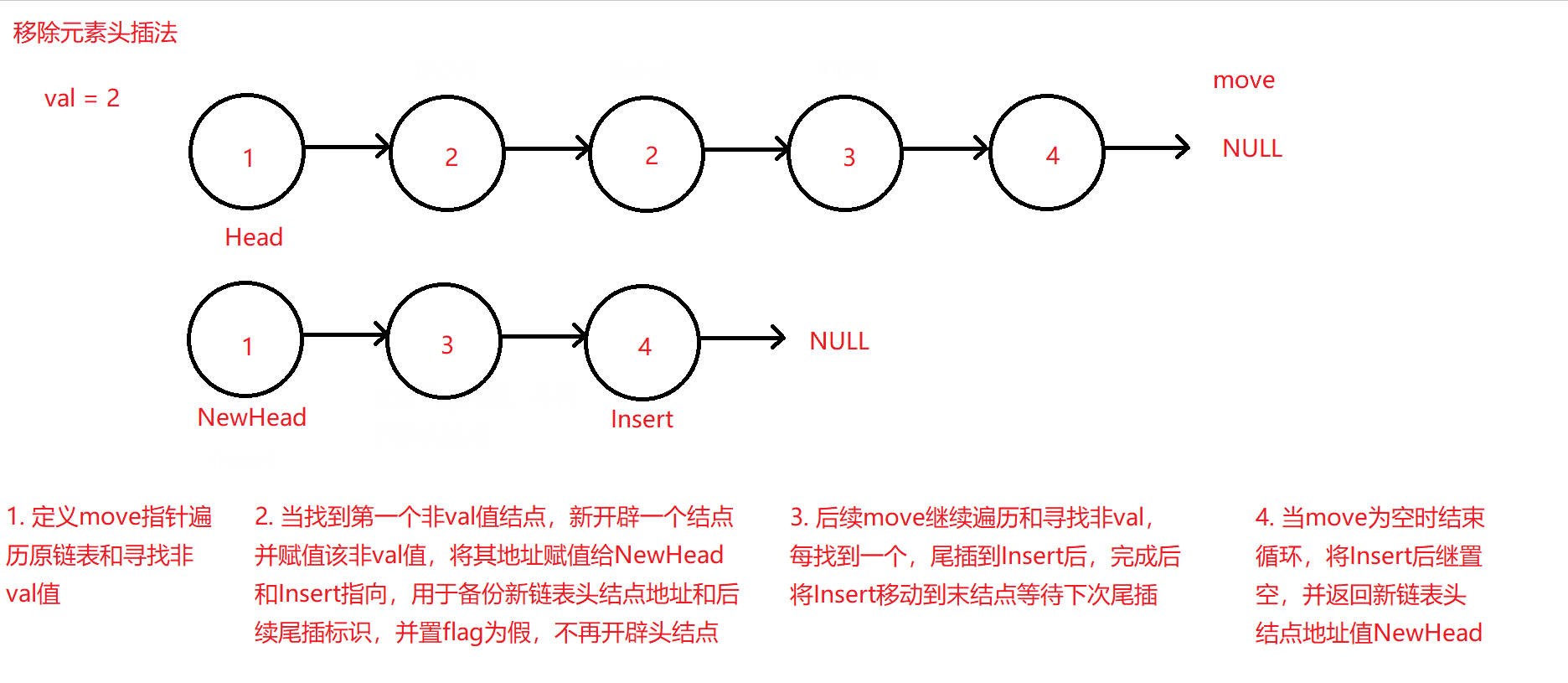
	if (NewHead == NULL)						//若没有任何非val结点，则返回空链表
	{
		return NULL;
	}
	Insert->next = NULL;						//若存在新链表，将insert的后续结点置空
	return NewHead;
}

函数传参为链表头结点地址，并传入一个需要移除的链表对应结点值val，该函数具有返回值，返回的是一个非原链表的新链表头结点地址值给主函数中新定义的指针，用于打印和观察尾插后的新链表。
函数开头对传入的链表头结点地址判空，这里值得注意的是，如果是日常刷OJ题时不建议使用assert来断言，因为断言方便用户调试时直接观察代码位于哪一具体位置出错，而在线刷题可能会给出空链表用例，所以判空断言不符合题目要求，改用较为柔性的if判断并返回NULL是更好的选择。
定义两个指针Insert和move，move主要用于遍历原链表和寻找非val值的结点，所以初始化为原链表头地址，Insert和NewHead用于新链表的尾插指针和需要返回的新链表头地址，初始化为空即可。再定义一个布尔变量flag，用于当第一个非val结点被move找到时作为新头地址的开辟，开辟完成后置假，因为头结点只需要开辟一次，后续循环只用在头地址后尾插即可。
每找到一个非val结点，就将move对应的该结点的数值move->data尾插pushback到新链表中，使用Insert充当临时头结点并将新开辟的结点尾插到Insert后，尾插完成后返回Insert充当的临时头结点再赋值给Insert，再将其指向新插入的新链表尾结点即可。

原理图如下：

测试用例

//case 1：空链表传参
SgL* n1 = NULL;
printf("原链表结构为：");
Print(n1);
int value = 1;
SgL* NewHead = PushBack_not_Val(n1, value);
printf("移除后的链表结构为：");
Print(NewHead);

//case 2：连续相同待消除值
SgL* n2 = BuyListNode(7);
SgL* n3 = BuyListNode(7);
SgL* n4 = BuyListNode(7);
n2->next = n3;
n3->next = n4;
printf("原链表结构为：");
Print(n2);
int value = 7;
SgL* NewHead = PushBack_not_Val(n1, value);
printf("移除后的链表结构为：");
Print(NewHead);

//case 3：不连续擦除
SgL* n1 = BuyListNode(1);
SgL* n2 = BuyListNode(2);
SgL* n3 = BuyListNode(3);
SgL* n4 = BuyListNode(1);
SgL* n5 = BuyListNode(4);
SgL* n6 = BuyListNode(5);
SgL* n7 = BuyListNode(1);
n1->next = n2;
n2->next = n3;
n3->next = n4;
n4->next = n5;
n5->next = n6;
n6->next = n7;
printf("原链表结构为：");
Print(n1);
int value = 1;
SgL* NewHead = PushBack_not_Val(n1, value);
printf("移除后的链表结构为：");
Print(NewHead);