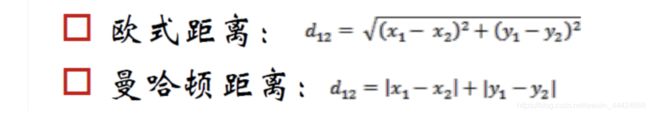数据仓库笔记

目录

第二章 数据仓库
第三章 数据预处理
第四章 特征化和区分
数据挖掘
第五章 关联规则挖掘
第六章 分类挖掘
第七章 聚类挖掘

第二章 数据仓库

1、B树索引

考题：为何B树等在数据库中广泛使用的索引技术无法直接被引入数据仓库？

1、B树要求属性必须具有许多不同的值，比如身份证号这种取值字段，取值范围很广，几乎没有重复。
2、B树要求查询应具有更简单的条件和更少的结果
3、创建B树的空间复杂度和时间复杂度很大

2、位图索引 BitMap Index

位图索引分为两种，简单位图索引和编码位图索引，考试时候会让你画简单位图索引。

（1）简单位图索引

对于每个属性，将属性中的不同取值生成不同的位向量！有几个不同的取值就有几个不同的位向量。如果数据表中某一元组的属性 值为 v，则在位图索引的对应行表示该值的位为 1，该行的其它位为 0。

例如：

如果我们要找买了b产品的女性，计算时候首先取出b产品和女性F向量做&操作

b：0 0 1 1 1 0 0 0

F：1 0 1 1 0 1 0 0

---

​ 0 0 1 1 0 0 0 0

发现第3位和第4位为1，表示第三行、第四行数据是我们要的结果

位图索引适合只有几个固定值的列，如性别、婚姻状况、行政区等等，对于性别，可取值的范围只有’男’,‘女’，并且男和女可能各站该表的50%的数据，这时添加B树索引还是需要取出一半的数据， 因此完全没有必要。如果某个字段的取值范围很广，几乎没有重复，比如身份证号，就不适合用位图索引，适合B树索引。

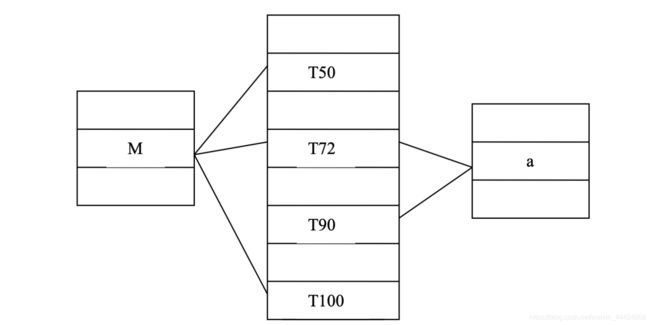
3、连接索引 Join Index

适用于复杂的查询！复杂的查询往往需要多表连接，使用连接索引能提高性能。考试时候要求画出连接索引怎么画？

先说下什么是事实表、维表。事实表就是你要关注的内容，比如各种销售数据，通常包含大量的行。维表就是你观察该事物的角度，你从哪个角度去查看这个内容？比如对于销售数据，可以从某个地区的来看，地区就是维度。

例如，在一个星型模式中，事实表 Sales 与维表 Customer 和 Item 三者之间的链接关系如图所示。

它们的链接索引表如图所示。

4、数据仓库存储策略

在逻辑模型设计的基础上确定数据存储结构、索引策略、存储分配和数据存放位置等与物理有关的内容，与数据库设计中大致相似。

常用技术

• 合并表
  表的连接操作消耗很多时间，将表合并后存放，可以节约连接的时间，这是以空间换时间的策略
• 数据序列
  将连续使用的数据连续存储，原先表示逻辑的部分可以继续存在
• 引入冗余
  此处特指将一个属性从一张表扩散到其它表的过程，这个过程中，冗余就可以节约访问的连接次数
• 表的物理分割
  类似逻辑设计阶段的数据分割，用拆分的表来表达原有逻辑意义上的一张表
• 生成导出数据
  如果某张表的统计数据被频繁访问，这部分聚集数据就可以另行记录
• 建立广义索引
  记录与“最”有关的统计结果。这部分数据非常小，又可以在数据刷新阶段直接建立，进行此类查询时就可以将统计操作转换为简单查找所以不用B树索引！

5、数据仓库

（1）数据仓库的出现？

建立数据仓库不是要替代传统的事务处理系统和数据库，而是在新的领域中更加适应分析型处理的需要。数据仓库正成为信息集成的主要手段之一。

其出现目的：

• 提高两个系统的性能
• 提高操作性数据库的事务吞吐量
• 两个系统中的数据结构、内容和用法可以不同

（2）数据仓库的特点/特征

• 面向主题

  主题就是企业中某一领域涉及到的分析对象，面向主题就是说：数据仓库内的信息是按照主题进行组织的。主题是要经过抽取得出的

• 集成

  全部数据放置在同一个地方，形成完整、一致的数据汇总

• 非易失

  数据仓库的数据与操作型数据环境隔离

• 时变

  数据仓库随时都是一个只读的备份，每隔一段时间完成一次对数据仓库的刷新

6、OLAP

OLAP即联机分析处理，通过专门的数据综合引擎，辅以更加直观的数据访问界面，在短时间内相应非数据处理专业人员的复杂查询要求。

（1）OLAP特点

• OLAP是面向特定问题的联机数据访问和分析
  OLAP是只读的工具，这是与SQL的巨大差异
• 通过对信息多种可能的观察形式进行快速、稳定一致和交互性的存取
  多个“维度”
• 允许决策人员对数据进行深入观察
  以人为主导

（2）OLAP的基本数据模型

• MOLAP
  多维数据库

• ROLAP

  用事实表的二维模型存放度量值，定义大量外关键字指向维度

  • 星形模型
  • 雪花模型

详细介绍ROLAP

• 星型模式

  • n维的多维表有一个事实表和n个维表增加一个新的维度，就增加一个维表，从而易于扩充
  • 应对多维查询时，依赖标准SQL将事实表与维表进行连接与聚集
  • 星型模式的优势在于架构一旦确定下来，影响架构的宏观因素就很少，可以以基本固定的方式进行优化

• 雪花模型

  • 对星型模式的扩展
    某些维表并不是单一的平面结构，所有维属性的地位并不等同
  • 优点
    • 更加适应人类的理解和观察
      内在的关联性通过将子维表分列而体现出来
    • 规范化的设计趋势节约存储空间
  • 缺点
    • 结构远比星型模式复杂
    • 额外进行的多次连接造成性能损失
    • 即使维数相同，表的结构也可能有很大差异
      难以优化

• 其它扩展模式

  • 星座模式
    通过公共维度连接多个星型模式
  • 雪暴模式
    通过公共维度连接多个雪花模型

7、数据立方体

数据立方体是一种多维数据模型，主要有星形模式、雪花模式和事实星座模式。

• 星形模式
  它是最常见的模式，它包括一个大的中心表（事实表），包含了大批数据但是不冗余；一组小的附属表（维表），每维一个。如下所示，从item、time、branch、location四个维度去观察数据，中心表是Sales Fact Table，包含了四个维表的标识符（由系统产生）和三个度量。每一维使用一个表表示，表中的属性可能会形成一个层次或格。
  

• 雪花模式
  它是星模式的变种，将其中某些表规范化，把数据进一步的分解到附加的表中，形状类似雪花。

• 事实星座

  允许多个事实表共享维表，可以看作是星形模式的汇集。如下所示，Sales和Shipping两个事实表共享了time、item、location三个维表。

  

在数据仓库中多用事实星座模式，因为它能对多个相关的主题建模；而在数据集市流行用星形或雪花模式

8、多维数据分析手段

• 切片

只看与该维成员相关的数据，就是降维

• 切块

可以认为是切片的复合操作，维度可能无法下降，但数据量得以减少

• 旋转

交换维度的排列顺序，获取全新的呈现方式。高维的旋转操作会很有用，交换了某些维度的焦点

• 上钻

将层次较低的数据集提高层次，上钻不会变更观察的主体

• 下钻

上钻的逆操作，降低数据层次，上钻与下钻并不能无限地进行下去，下界为原子层。

• 其它操作
  • 跨钻
    同步地对多个多维模型进行上钻或下钻，方便进行多个事实的对比
• 钻透
  • 下钻到数据立方体最低细节后，继续细化到数据仓库/数据库的关系型表格
  • 可以发现一些错误

9、数据仓库的设计

见ppt

第三章 数据预处理

1、数据预处理过程

• 数据清洗

  • 缺失值、噪声、非一致

• 数据集成

  • 模式集成、发现冗余、数据值冲突检测和处理

• 数据变换

  • 光滑、聚集、泛化、规范化、属性构造

• 数据规约

  • 数据立方体聚集、属性子集选择、维度规约、数值规约、离散化和概念 分层产生

• 数据离散化

  • 数值数据

    • 分箱、直方图、聚类、基于熵的离散化、基于直观划分离散化

  • 分类数据

    • 用户或专家在模式级显示说明属性偏序，层次高，属性值个数越少

2、数据清洗

噪声数据：测量变量时出现的随机错误或是差异，出现原因可能是属性值不正确（数据收集工具问题、数据的输入或传输问题等）以及数据不完整、不一致、重复记录产生的

针对噪声数据的处理方法：分箱/分桶、聚类、人工检查、回归

简单离散化方法：分箱

• 等宽分箱 equip-width
  • ​ 将范围分为相等大小的N个间隔
  • ​ 间隔的宽度将为：W =（B-A）/ N （属性最高值-最低值）/N个间隔
• 等深分箱 equip-depth
  • 分成N个间隔，每个间隔样本数相同

分箱后需要平滑数据，主要方法有：按箱平均值平滑、按箱中值平滑、按箱边界平滑

3、数据集成与变换

数据集成主要讲了去除冗余啥的，这边主要看数据转换的方式

（1）数据变换

• 平滑
  • 消除噪声数据
• 聚合
  • 汇总数据
• 泛化
  • 概念层次爬升，就是概念化
• 归一化
  • 缩放数据到指定范围内
• 属性/特征构造

（2）归一化的三种方式

• min-max normalization

  

  value’ =（value-最小值）/（最大值-最小值）

  

• Z-score normalization

  Z标准化也叫标准差标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。
  

• normalization by decimal scaling

  进制缩放归一化。这种方法通过移动数据的小数点位置来进行标准化。小数点移动多少位取决于属性A的取值中的最大绝对值。公式中j是满足条件的最小整数。
  
  例如 假定A的值由-986到917，A的最大绝对值为986，为使用小数定标标准化，我们用每个值除以1000（即，j=3），这样，-986被规范化为-0.986。
  

4、数据规约

​ Data Reduction，即数据规约，PPT中提到了4中策略

• 数据立方体聚合
• 降维
• Numerosity reduction
• 离散化和概念层次生成

观察往年试卷，考过离散化

​ maxdiff：先给数据排序，给定β个桶或是分组，相邻数据的最大差是β-1，超过这个最大差就不能放进一个桶。

例子：

有个疑惑，最小方差每组算出来为什么要x2？

离散化的其他方法

• 基于熵的离散化 Entropy-based discretization

  给定一组样本S，如果使用边界T将S划分为两个区间S1和S2，则划分后的熵为
  

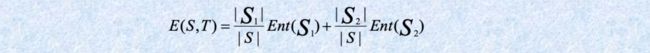
  选择在所有可能的边界上使熵函数最小的边界作为二进制离散化。该过程将递归应用于获得的分区，直到满足某些停止条件为止。
  

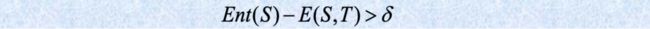
• 3-4-5规则

  3-4-5规则可用于将数字数据分段为相对均匀的“自然”间隔。

  看这个博客！

  • 如果间隔的最高有效位数涵盖3、6、7或9个不同的值，则将范围划分为3个等宽间隔
  • 如果它的最高有效位涵盖2、4或8个不同的值，请将范围划分为4个间隔
  • 如果它的最高有效位涵盖1、5或10个不同的值，请将范围划分为5个间隔

第四章 特征化和区分

废话

数据挖掘

1、数据挖掘

（1）数据挖掘是什么？

数据挖掘=数据库里的知识发现，在大量的、完整的数据中进行挖掘，总结规律、得出知识，来指导客观世界。

（2）数据挖掘基本概念

• 模式
  • 任何用高级语言表达一定逻辑含义的信息都是模式（信息+判断）
• 知识
  • 满足用户对客观评价标准（支持度/置信度……）和主观评价标准要求的模式
• 置信度 condidence
  • 某个数据集上，模式成立的程度，例如在购买面包和黄油的顾客中，大部分的人同时也买了牛奶，该模式的置信度为：同时购买面包、黄油、牛奶的顾客人数占同时购买面包、黄油的顾客人数的百分比。
  • 置信度不是固定的
  • 没有足够的置信度，模式也不能称为知识
• 支持度 support
  • 某一数据集上，模式被用户关注的程度，也叫做兴趣度
• 非平凡性
  • 平凡的知识不是数据挖掘的目标，因为这样的知识已经成为常识，我们要找的是不平凡的知识

（3）数据挖掘和数据仓库啥关系？

• 数据挖掘原本建立在数据库的基础之上
• 产生数据仓库技术后
  由于数据仓库中的数据都是经过抽取、整理和预处理后的综合数据，因而数据挖掘工作可以在数据仓库上直接运行，任务相对来说会简单很多，但并不代表数据挖掘可以无缝地架设在数据仓库之上

（4）数据挖掘步骤

• 数据的集成

  • 没数据怎么行？一般都集成到数据仓库

  • 在数据仓库要对数据预处理

    • 清洗、集成、转换、减少

• 数据规约

  • 用于数据挖掘的数据量非常巨大，数据规约可以减低数据量，提高数据挖掘操作的性能

  • 常见的数据规约技术

    • 数据立方体计算
    • 挖掘范围的选择
      • 在不影响挖掘结果的前提下，尽可能地选取那些与挖掘操作有关的属性集，去除明显无关的因素，或由于法规、风俗等原因，即使有相应的分析结果也无法应用的
      • 时间范围或备份内容上的选择
    • 数据压缩
      减低数据的规模，节省存储空间开销和数据通讯开销，如果采用的数据挖掘算法不需要解压就可直接对压缩数据进行挖掘，数据压缩技术将非常有用
    • 离散化处理
      将属性值的连续区域划分为若干个区域，用每个区域的标识代替原来的值，以减低该属性上属性值的个数，也可利用这种数据规约技术来自动地建立该属性的概念层次树

• 挖掘

  • 挖掘方法
    • 关联规则挖掘–第五章
    • 分类挖掘–第六章
    • 聚类挖掘–第七章

• 表示

  • 可以包括文字、图形、表格、图标等可视化形式

第五章：关联规则挖掘

1、关联规则

资料

• 关联规则用于表示事务数据库中诸多属性之间的关联程度

• 关联规则挖掘则是利用数据库中的大量数据通过关联算法寻找属性间的相关性

• 属性在这里被称为 项

  若干个属性所构成的属性集被称为一个 项集

  例：超级市场

  在购买商品A的客户中有90%的人会同时购买商品B，则可用关联规则表示为：

  R1：A->B 表示一条规则
  

• A->B与B->A的支持度是相同的，但置信度通常不同

• 任意组合均能构成关联规则

  为了发现有意义的关联规则，需要给定两个阈值：

  最小支持度 和 最小置信度

  • 满足最小置信度和最小支持度的规则为强规则，否则为弱规则
  • 关联规则挖掘的实质是在数据库（数据仓库）中寻找强规则

支持度：$Sup(X)=\frac{Sum(X)}{N}$

置信度：$Conf(X\to Y)=\frac{Sup(X\cup Y)}{Sup(X)}$

2、Apriori算法

推荐博客

（1）基本概念

• 项
  在数据库中出现的属性值，每一个属性值构成一个项
• 项集
  在数据库中出现的属性值的集合
• k-项集
  由k个项构成的项集
• 频繁项集
  • 该项集在数据库中出现的频度满足用户规定的最小支持度的要求
  • 即同时含有该项集中的所有属性值的记录数 占 所有记录数的百分比 大于等于用户规定的最小支持度
• 关联规则一定是在满足用户的最小支持度要求的频繁项集中产生的
  • 关联规则的挖掘过程也就是在数据库中寻找频繁项集的过程
  • 寻找频繁项集过程中，遵循每个频繁项集的任一子集也是一个频繁项集

（2）寻找频繁项集的方法

• 寻找一阶频繁项集C1
  除去非频繁项集，得到L1
• 从L1生成二阶超集，即候选频繁项集C2
  除去非频繁项集，得到L2
• 从L2生成三阶超集C3
  除去暂时不需要考虑的更高阶超集
  除去非频繁项集，得到L3
• ……

最后得到的频繁项集是L1、L2、L3……的并

Apriori算法：执行算法之前，用户需要先给定最小的支持度和最小的置信度。生成关联规则一般被划分为如下两个步骤：

1. 利用最小支持度从数据库中找到频繁项集。

   给定一个数据库 D ，寻找频繁项集流程如下图所示
   

   ​ 首先寻找一阶频繁项集C1，C1中，{1}的支持度为2/4 = 0.5（数据库D中一共四条事物，{1}出现在其中的两条事物中），C1中的其他几个也是这么计算的，假设给定的最小支持度 $SU{P}_{min}=0.5$，{4}就被排除了，得到L1。

   ​ 接下来从L1生成二阶超集，即候选频繁项集C2，除去非频繁项集（也就是低于SUP_min = 0.5的），得到L2。

   ​ 从L2生成三阶超集C3，除去暂时不需要考虑的更高阶超集，除去非频繁项集，得到L3

   ​ 我们可以看到 itemset 中所包含的 item 是从 1 增长到 3 的。并且每次增长都是利用上一个 itemset 中满足支持度的 item 来生成的，这个过程称之为候选集生成

2. 利用最小置信度从频繁项集中找到关联规则。（3）中内容

   同样假定最小的置信度为 0.5 ，从频繁项集 {2 3 5} 中我们可以发现规则 {2 3} ⇒ {5} 的置信度为 1 > 0.5 ，所以我们可以说 {2 3} ⇒ {5} 是一个可能感兴趣的规则。（这里看不懂的话看一下上面置信度公式就懂了）

如何发现全部的频繁项集？

包含N种物品的数据集共有2^N-1种不同的项集，例如包含4种物品的全部项集：

（3）生成关联规则

• 由此确定关联规则的生成算法：（输入参数：数据集和一个频繁项集）

• 针对频繁项集{A,C}可以构造两条规则

  R1：A->C
  R2：C->A
  

  一阶频繁项集无法构造关联规则，只能得到平凡知识
  将每个频繁项集分为左右两部分，穷举即可以得到

• 对这些规则进行测试（依次计算置信度，用到的支持度数据在生成频繁项集的时候都存下来了）

• 通过预先设定的阈值对关联规则进行过滤

• 合并所有第一个列表中的剩余规则，创建第二个规则列表，其中规则右部包含两个元素

• 对第二个列表中的规则进行测试

• 过程重复到N为止（或者无法产生新规则）

• 最后剩余的关联规则上升为知识，用于决策支持

比如上面那个例子{2,3,5}，就可以分为 {2}–>{3,5} 与 {2,3}–>{5}，然后计算置信度，也就是

置信度con(X–>Y) = (X U Y)/X。这里有个窍门

假设最小置信度为p，且规则0,1,23并不满足最小置信度要求，即 P(0,1,2,3)/P(0,1,2)

（5）Apriori算法的优化方法

由于算法是时间开销花在数据库的多次扫描上，主要的优化方法有：

• 数据库的划分（Partitioning）方法

  针对硬件限制进行优化

  虽然置信度和支持度指标可能有变化，但

  所有关联规则一定都会出现在各个划分中

  划分可能导致产生的关联规则数量过大，提高阈值又会损失原有的规则

  • 每一部分都能全部放在内存中进行扫描
  • 最后对得到的所有频繁项集进行归并

• 利用Hash方法筛选2阶频繁项集
  将每个项哈希到哈希表里，从而大量地过滤不需要的候选集

• 利用采样数据集得到可能成立的规则，再利用数据库中的剩余数据验证这些规则的正确性
  由于无法保证结论的正确性，此方式未必靠谱

• 减少每一遍扫描所处理的记录数

  如果一条记录不含有长度为k的频繁项集，那么这条记录也不可能含有长度为(k+1)的频繁项集
  

  得到所有k阶频繁项集后，以后的每次扫描就不必再访问上述的记录，从而逐步减少被扫描的记录数

3、FP-Growth算法

（1）介绍

FP核心：利用FP树递归地增长频繁模式路径（分治）

FP优点：去除了不相关的信息；出去节点连接和计数规模比原数据库小；快速；将发现长频繁模式的问题转换成递归地搜索一些较短的模式。

关联分析算法，它采取如下分治策略：将提供频繁项集的数据库压缩到一棵频繁模式树（FP-Tree），但仍保留项集关联信息；该算法和Apriori算法最大的不同有两点：第一，发现频繁项集而不产生候选 ，第二，只需要两次遍历数据库，大大提高了效率。但是FP-Growth算法只能用来发现频繁项集，不能用来发现关联规则。

（2）算法伪代码

详细见博客

（3）PPT例子

博客

给定数据库D以及min_sup

1. FP-Tree构建——第一步

   第一步：扫描数据库，得到一阶频繁项集。由于min_sup = 0.5，所以至少出现3次，低于3次的直接不考虑了，得到项集如下

2. FP-Tree构建——第二步

   第二步：以频率递减的顺序对频繁项进行排序，注意里面的顺序
   

3. FP-Tree构建——第三步

   每个事务中的数据项按降序依次插入到一棵以NULL为根结点的树中，这样所有的ordered frequent items都保存在了树中。，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。
   

4. FP-Tree挖掘——第一步

   ​ 得到了FP树和项头表以及节点链表，我们首先要从项头表的底部项依次向上挖掘。对于项头表对应于FP树的每一项，我们要找到它的条件模式基。条件模式基是以我们要挖掘的节点作为叶子节点所对应的FP子树。得到这个FP子树，我们将子树中每个节点的的计数设置为叶子节点的计数，并删除计数低于支持度的节点。从这个条件模式基，我们就可以递归挖掘得到频繁项集了。
   
   
   意思是item是x的时候，也就是后缀是x，他的前缀有哪些？出现次数是多少个。比如后缀是c，前缀是f，出现了3次；再比如后缀是b的，他的前缀有fca（1次），f（1次），c（1次），就这个意思

5. FP-Tree挖掘——第二步

   将得到的FP子树的每个节点的计数设置为叶子节点的而计数，并删除计数低于支持度**（这里至少是3）**的节点。我们就可以得到频繁项集。

一定要看这个例子

举例叶子结点是一阶的情况

从底向上挖掘。先看p，它的频繁项集为{f:2,c:3,a:2,m:2,b:1,p:3}、前面5个代表条件模式基（大白话就是每个出现了几次，比如c出现了2+1次）,f、a、m、b的个数低于3个，低于我们要求的支持度，删除，合并一下，得到p结点的频繁二项集{c:3,p:3}，p对应的最大的频繁项集为频繁二项集。

再看m，它的频繁项集为f:3,c:3,a:3,b:1,m:3}，删除b，得到m的频繁四项集{f:3,c:3,a:3m:3}

再看b，它的频繁项集为{f:2,c:2,a:1,b:3}，删除fca，他只是个平凡知识，empty

再看a，它的频繁项集为{f:3,c:3,a:3}，这就是它的三阶频繁项集

再看c，…

老师举的例子（一阶）

一阶结果，明显和我们刚才做的思路结果一致

举例叶子结点是二阶及以上的情况，同样思路

第六章：分类挖掘

1、数据分类

• 通过分析训练数据样本，产生关于类别的精确描述
• 这种类别通常由分类规则组成，可以用来对未来的数据进行分类和预测

首先为每一个数据（记录）打上一个标记，即按标记对数据（记录）进行分类，而分类分析则是对每类数据（具有相同标记的一组记录）找出其固有的特征与规律。

2、数据分类的步骤

建立一个模型，描述给定的数据类集或概念集，通过分析由属性描述的数据库元组来构造模型

• 用于建立模型的元组集称为训练数据集，其中每个元组成为训练样本
  训练样本的性质与待分析样本本质上没有差别，都是在实际环境中累积得到的数据
• 每个训练样本属于一个预定义的类，由类标号属性确定
• 由于给出了类标号属性，因此该步骤又成为有指导的学习
  需要知道分类的数量，与对应分类对人来说的意义
  如果训练样本的类标号是未知的，则称为***无指导的学习（聚类）***
• 学习模型可以用分类规则、决策树和数学公式的形式给出

使用模型对数据进行分类

• 评估模型的分类准确性
  训练数据和测试数据性质应当是一样的，但不能是两份相同的数据
  评价的标准包括正确性、效率、可理解性
• 对类标号未知的元组按模型进行分类

3、分类分析方法

是一种特征归纳的方法，将每类数据共有的特性抽取以获得规律性的规则，目前有很多分析方法，看了下往年试卷就考了决策树和朴素贝叶斯

• 决策树——考试考ID3
• 朴素贝叶斯
  • 通过前验概率和后验概率，决定某一特定样本属于标签中某一分类的概率
    概率的值根据训练样本提供
  • 贝叶斯方法得到的结果不唯一，并且能提供相应结果的概率大小
  • 贝叶斯方法计算复杂
    在各属性独立时，贝叶斯方法的计算可以简化

以上两种方法基于信息论，具有很好的可剪枝性

K邻近算法也考了。。。不难，看一下就好。

4、决策树——ID3算法

（1）概念

又称为判定树，是运用于分类的一种树结构

• 根据对一个判定进行拆分，连接到下一个判定或结论，构成的关系就是一棵决策树

• 每个内部结点代表对某个属性的一次测试

• 每条边代表一个测试结果

• 叶结点代表某个类或者类的分布

• 最上面的结点是根结点

• 通过对信息量的计算，判断每个属性对分类所作判断的贡献大小
  将一个集合S拆分为S1和S2，其信息量大小有以下关系：

  I(S)≥I(S1)+I(S2)
  （在属性对分类不起任何作用时取等号）
  属性的信息增益A=I(S)-[I(S1)+I(S2)]
  

  将贡献最优的属性放在顶层，迭代进行

  • 中止条件
    • 训练数据集为空
    • 分类已经确定
      I(S)=0
    • 属性已经用完，仍然无法确定地分类

（2）ID3算法

推荐博客

一种基于决策树的算法，根据信息增益，自顶向下贪心建树，信息增益用于度量某个属性对样本集合分类的好坏程度，我们要选择具有最高信息增益的属性。基于训练对象和已知类标号创建决策树，以信息增益为度量来为属性排序。

两个类标记：P（假设有p个元素） 和 N（假设有n个元素），用来判断任一元素属于P还是N的信息量为：

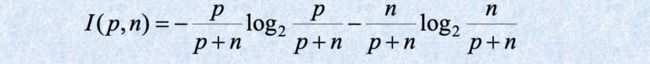
根据属性A将集合S划分为集合{S1，S2，…，Sv}，在每个Si中，属于类P的元素为Pi，属于N的元素为ni，用来区分的信息量（熵）为

计算属性A的信息增益 Gain(A)

直接看PPT例子

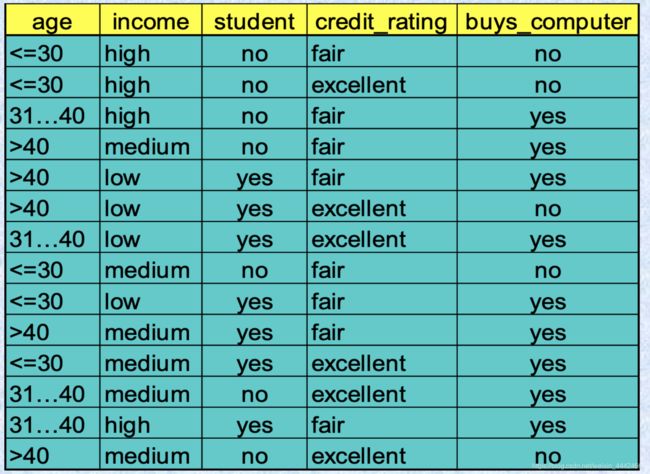
给了这个一张表，按照哪个属性来分类？

这个例子中

• P：buys_computer = “yes” ,N:：buys_computer = “no”,一个14个数据,p:9个，n:5个

• I(p, n) = I(9, 5) =0.940

• age属性的熵的计算

  • 根据age属性，把整个输入集S划分成了三部分：<=30岁，31～40岁，>40岁
  • <=30岁的5人中，yes 2人，no 3人，那就是 5/14*I(2,3)
  • 31~40岁的4人中，yes 4人，no 0人，那就是 4/14*I(4,0)
  • 大于40岁的5人中，yes 3人，no 2人，那就是5/14*I(3,2)
  • 求和可得age属性的熵E(age)

• Gain(age) = I(9,5) - E(age)

• 按照同样的方法求Gain(income)、Gain(student)、Gain(credit_rating)

结果$Gain(age)=0.25>Gain(student)>Gain(credi{t}_{r}ating)>Gain(income)$

这样就知道哪个属性的排序了，然后对age分类下的三种情况

• 在<30情况下，计算信息增益，发现student的信息增益最大，则将student设为节点；

• 在30-40之间只有yes，所以不需要计算

• 在>40情况下，发现credit rating的信息增益最大，则设它为节点。
  

5、朴素贝叶斯

朴素贝叶斯算法的数学基础都是围绕贝叶斯定理展开的，因此这一类算法都被称为朴素贝叶斯算法。分类原理是通过对象的先验概率，利用贝叶斯公式计算出后验概率，即对象属于某一类的概率，选择具有后验概率最大的类作为该对象所属的类。下面是贝叶斯公式，要使P(C|X)最大（先验概率），则要使得P(X|C)·P©最大（后验概率），

朴素贝叶斯就是假设属性是独立的情况，特征（属性）之间互相独立

例1

网球比赛示例，p代表能进行比赛，n代表不能进行比赛，X =

例2：贝叶斯信念网络/概率网络

就是将贝叶斯推理与属性之间的因果关系相结合

PPT上例题直接看这博客

首先计算患心脏病的先验概率

α：E的可能取值，β：D的可能取值

由于朴素贝叶斯假设属性之间的独立，即E与D独立，则：P(E=α,D=β) = P(E=α) * P(D=β)

那就是四种情况加起来，PPT顺序错了

用了这些数据

​ 结论：不得心脏病的概率更大

BP=high的情况下，利用同样方法计算高血压数据，它与HD有关

结论：如果血压高，得心脏病概率更大

在BP=high,D=healthy,E=yes的情况下HD的概率（血压高，饮食健康，做运动的心脏病的概率）

第七章：聚类挖掘

1、聚类分析

聚类分析是在数据中发现数据对象之间的关系，将数据进行分组，组内的相似性越大，组间的差别越大，则聚类效果越好。

• 又称集群分析，它是研究分类问题的一种多元统计方法
• 分为距离聚类和相似系数聚类，即定义相似程度的两种方式，实际上没必要严格地区分
• 没有筛选出一小部分数据，经过处理得到模型，再以此模型进行通用处理的两个阶段

与分类分析的混合使用

由于聚类分析的时间复杂度与整体样本数量有关，因此可以抽样一部分数据进行聚类分析，得到结果后，对每个聚类进行概念规则挖掘，人为确定一些概念规则，再以此规则对剩余数据进行分类

• 聚类分析输入的是没有被标记的记录，系统按照一定的规则合理的划分记录集合
  相当于给记录打标记，但分类标准不是用户确定的
• 然后采用分类方法对数据进行分析，并根据分析结果重新对原来的记录集合进行划分，进而再进行一次分类分析
• 如此循环往复，直到获得满意的分析结果

2、主要的聚类方法

• 基于划分方法

  一些场景中，划分聚类的数量k是知道的；即使不知道划分聚类的数量，也是可以以穷举的方法进行确定的（1≤k≤N）

  • 随机地选择k个数据
  • 将其它所有数据打上距离最近的标记
    完成一次迭代
  • 根据当前聚类选择一个实际（或虚拟）的数据点
    具有代表性的
  • 第二次迭代，根据选择的点再进行一次划分
    代表性的数据点继续发生变化
  • 如此循环往复，直到每个数据的聚类不再发生变化为止
  • 代表数据点的选择问题
    • 如果选择实际的数据点作为代表，选择的标准难以确定
    • 如果选择虚拟的数据点作为代表，数据点又可能没有意义,需要根据实际任务选择类型

• 基于层次的方法

  将相似程度最大的两个数据合并，以一个虚拟数据点作为其代表，重复进行计算

  • k值是可以不必给定的
    以聚类内的相似程度和聚类间的相异程度作为指标
  • 没有迭代的过程，结果可能并不精确

ps：往年考了K-means算法和 凝聚式层次式距离算法

3、K-means聚类算法

这是一种基于划分的距离技术，它将各个聚类子集内的所有数据样本的均值作为该聚类的代表点，算法的主要思想是通过迭代过程把数据集划分为不同的类别，从而使生成的每个聚类内紧凑，类间独立。

考试会出现的距离主要是曼哈顿距离

k-means算法
输入：簇的数目k和包含n个对象的数据库。
输出：k个簇，使平方误差准则最小。
算法步骤： 
  1.为每个聚类确定一个初始聚类中心，这样就有 K 个初始聚类中心。 
  2.将样本集中的样本按照最小距离原则分配到最邻近聚类  
  3.使用每个聚类中的样本均值作为新的聚类中心。
  4.重复步骤2.3直到聚类中心不再变化。
  5.结束，得到K个聚类

面向考题学习【2012期末】

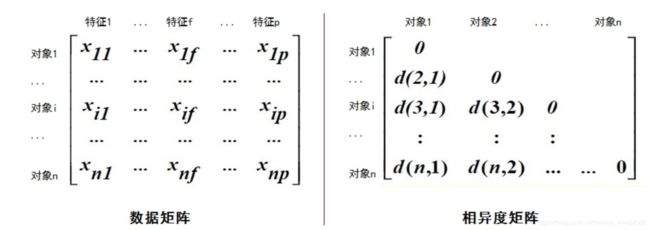
第一个问题：要求给出相异矩阵，相异度矩阵（存储n个对象两两之间的近似性）。同时，也提出了一个表示n个对象的矩阵，即数据矩阵（用p个变量来表示n个对象），如下图。

我们只需要把每一元组的x、y值带进曼哈顿距离算一下就是答案了-_-

第二个问题：对数据集进行聚类，给定了簇的数量为k = 3，给定了三个起始中心点（3，5）、（2，6）、（3，8），一共12个点（对象），那么对于剩余的9个点（对象），根据其与各个簇中心的距离，将它赋给最近的簇。大白话就是对剩下的点，用曼哈顿距离算一下它和哪个中心点近，就把它归类过去。

就看前三列，取最小的放入对应聚类

(1,4,6,7,11,12)
(2,9)
(3,5,8,10)

重新调整三个聚类的中心点

(1,4,6,7,11,12)	--> x = (3+3+4+9+5+4)/6 = 4.6;y = (5+4+5+1+2+2)/6 = 3.17	(4.6,3.17)
(2,9) --> x = (2+1)/2 = 1.5;y = (6+6)/2 = 6 (1.5,6)
(3,5,8,10) x = (3+7+4+6)/4 = 5;y=(8+7+10+8)/4 = 8.25 (5,8.25)

然后再每个点算到三个中心点的距离，得到三个聚簇

一直这么算直到聚簇内不变化

4、凝聚式层次式距离算法

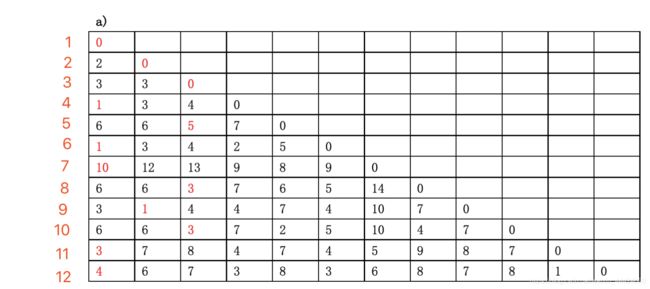
【2014期末】b问

把每个点与其他点的距离都算出来，选距离最小的作为初始的那两个点，聚到一起之后算它们的中心点，然后这个中心点和其他n-2个点再算距离，再挑出两个最小的聚到一起，再算中心点…一直到所有的都聚进来。最后我们想要聚成几类就在倒数第几步砍一刀。比如要求聚成两类，在step3砍一刀，一类是cde，另一类是ab。

初始a问曼哈顿距离

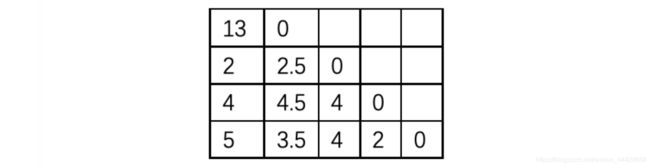
聚1和3，再计算其他点到新点距离

聚135，再计算其他点到新点距离

聚1352，最后聚成12345