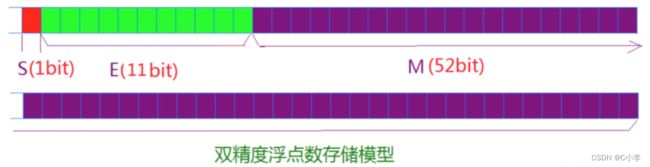
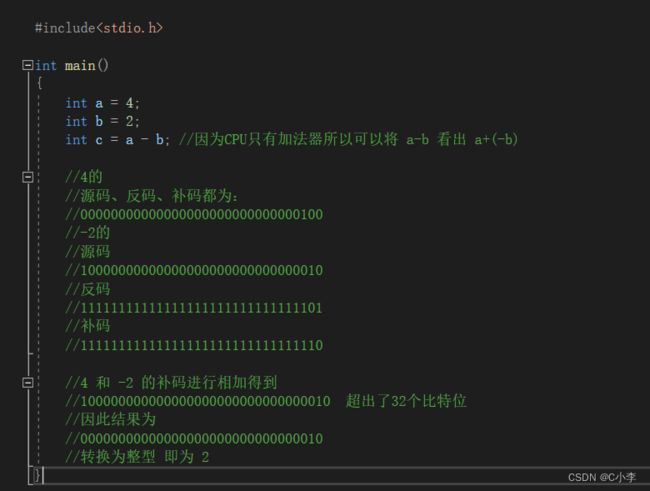
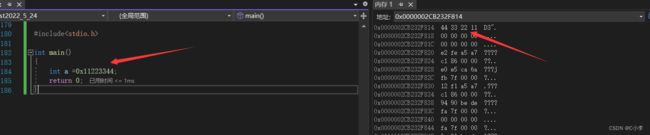
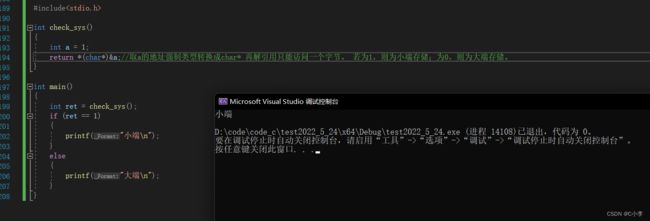
一、什么是宏函数?通过宏定义的函数是宏函数。如下,编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
C语言如何定义宏函数?
小九格物
c语言
在C语言中,宏函数是通过预处理器定义的,它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为,但它们不是真正的函数,因为它们在编译时不会进行类型检查,也不会分配存储空间。宏函数的定义通常使用#define指令,后面跟着宏的名称和参数列表,以及宏展开后的代码。宏函数的定义方式:1.基本宏函数:这是最简单的宏函数形式,它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
学点心理知识,呵护孩子健康
静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所,超越教育与技术的思考》的讲座。今天又重新学习了一遍,收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题,她说心理健康的一些基本命题,我们与我们通常的一些教育命题是不同的,她还举了几个例子,让我们明白我们原来以为的健康并非心理学上的健康。比如如果
c++ 的iostream 和 c++的stdio的区别和联系
黄卷青灯77
c++算法开发语言iostreamstdio
在C++中,iostream和C语言的stdio.h都是用于处理输入输出的库,但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系:区别1.编程风格iostream(C++风格):C++标准库中的输入输出流类库,支持面向对象的输入输出操作。典型用法是cin(输入)和cout(输出),使用>操作符来处理数据。更加类型安全,支持用户自定义类型的输入输出。#includeintmain(){in
ArcGIS栅格计算器常见公式(赋值、0和空值的转换、补充栅格空值)
研学随笔
arcgis经验分享
我们在使用ArcGIS时通常经常用到栅格计算器,今天主要给大家介绍我日常中经常用到的几个公式,供大家参考学习。将特定值(-9999)赋值为0,例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值(如0)Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值,其他保留原值SetNull("raster"==
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
回溯 Leetcode 332 重新安排行程
mmaerd
Leetcode刷题学习记录leetcode算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets,其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK(肯尼迪国际机场)出发的先生,所以该行程必须从JFK开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。例如,行程[“JFK”,“LGA”]与[“JFK”,“LGB
Python数据分析与可视化实战指南
William数据分析
pythonpython数据
在数据驱动的时代,Python因其简洁的语法、强大的库生态系统以及活跃的社区,成为了数据分析与可视化的首选语言。本文将通过一个详细的案例,带领大家学习如何使用Python进行数据分析,并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前,我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
2019-12-22-22:30
涓涓1016
今天是冬至,写下我的日更,是因为这两天的学习真的是能量的满满,让我看到了自己,未来另外一种可能性,也让我看到了这两年这几年的过程中我所接受那些痛苦的来源。一切的根源和痛苦都来自于人生,家庭,而你的原生家庭,你的爸爸和妈妈,是因为你这个灵魂在那一刻选择他们作为你的爸爸和妈妈来的,所以你得接受他,你得接纳他,他就是因为他的存在而给你的学习和成长带来这些痛苦,那其实是你必然要经历的这个过程,当你去接纳的
将cmd中命令输出保存为txt文本文件
落难Coder
Windowscmdwindow
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码,无可厚非,我们有必要保存我们的炼丹结果,但是复制命令行输出到txt是非常麻烦的,其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是:运行指令>输出到的文件名称或者具体保存路径测试下,我打开cmd并且ping一下百度:pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出:如果你再
四章-32-点要素的聚合
彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记,使用的openlayers5.3.xapi。源码见1032.html,对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
GitHub上克隆项目
bigbig猩猩
github
从GitHub上克隆项目是一个简单且直接的过程,它允许你将远程仓库中的项目复制到你的本地计算机上,以便进行进一步的开发、测试或学习。以下是一个详细的步骤指南,帮助你从GitHub上克隆项目。一、准备工作1.安装Git在克隆GitHub项目之前,你需要在你的计算机上安装Git工具。Git是一个开源的分布式版本控制系统,用于跟踪和管理代码变更。你可以从Git的官方网站(https://git-scm.
HTML网页设计制作大作业(div+css) 云南我的家乡旅游景点 带文字滚动
二挡起步
web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
Web前端开发技术描述网页设计题材,DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML:结构CSS:样式在操作方面上运用了html5和css3,采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript:做与用户的交互行为文章目录前端学习路线
Day1笔记-Python简介&标识符和关键字&输入输出
~在杰难逃~
Pythonpython开发语言大数据数据分析数据挖掘
大家好,从今天开始呢,杰哥开展一个新的专栏,当然,数据分析部分也会不定时更新的,这个新的专栏主要是讲解一些Python的基础语法和知识,帮助0基础的小伙伴入门和学习Python,感兴趣的小伙伴可以开始认真学习啦!一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码,再通过语言处理程序执行向计算机发送指令,让计算机完成对应的工作,编程
【JS】执行时长(100分) |思路参考+代码解析(C++)
l939035548
JS算法数据结构c++
题目为了充分发挥GPU算力,需要尽可能多的将任务交给GPU执行,现在有一个任务数组,数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务,一次执行耗时1秒,在保证GPU不空闲情况下,最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数,取值范围[1,10000]第二个参数为任务数组长度,取值范围[1,10000]第三个参数为任务数组,数字范围
人工智能时代,程序员如何保持核心竞争力?
jmoych
人工智能
随着AIGC(如chatgpt、midjourney、claude等)大语言模型接二连三的涌现,AI辅助编程工具日益普及,程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作,也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作,还是广泛学习以适应快速变化的技术环境?又或者,我们是否应该将重点转向AI无法轻易替代的软技能?让我们一起探讨程序员
node.js学习
小猿L
node.jsnode.js学习vim
node.js学习实操及笔记温故node.js,node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vuereactangular离不开node.jsnode.js是什么官网:node.js是一个开源的、跨平台的运行JavaScript的运行
阶段总结反思
轻争
马上就要进入10月份了,今天做一下前段时间的总结和反思。前段时间,日更、英语、健身、护肤坚持的比较好。阅读、书法坚持的不好。1.中间被迫停更半个多月,其余时间一直在坚持日更挑战。偶尔也有不想写的时候,就做一下摘抄。因为阅读(输入)没跟上来,所以写作(输出)质量有待进一步加强。2.英语做到了一周至少学习5天,每次不少于30分钟,但是小班课没有跟上更新速度,下一步要争取利用零碎时间补听小班课。3.减肥
ARM驱动学习之基础小知识
JT灬新一
ARM嵌入式arm开发学习
ARM驱动学习之基础小知识•sch原理图工程师工作内容–方案–元器件选型–采购(能不能买到,价格)–原理图(涉及到稳定性)•layout画板工程师–layout(封装、布局,布线,log)(涉及到稳定性)–焊接的一部分工作(调试阶段板子的焊接)•驱动工程师–驱动,原理图,layout三部分的交集容易发生矛盾•PCB研发流程介绍–方案,原理图(网表)–layout工程师(gerber文件)–PCB板
ARM驱动学习之5 LEDS驱动
JT灬新一
嵌入式C底层arm开发学习单片机
ARM驱动学习之5LEDS驱动知识点:•linuxGPIO申请函数和赋值函数–gpio_request–gpio_set_value•三星平台配置GPIO函数–s3c_gpio_cfgpin•GPIO配置输出模式的宏变量–S3C_GPIO_OUTPUT注意点:DRIVER_NAME和DEVICE_NAME匹配。实现步骤:1.加入需要的头文件://Linux平台的gpio头文件#include//三
ARM驱动学习之4小结
JT灬新一
嵌入式C++arm开发学习linux
ARM驱动学习之4小结#include#include#include#include#include#defineDEVICE_NAME"hello_ctl123"MODULE_LICENSE("DualBSD/GPL");MODULE_AUTHOR("TOPEET");staticlonghello_ioctl(structfile*file,unsignedintcmd,unsignedlo
展现思维导图魅力,不断挖掘人生宝藏
思维导图讲师Mandy
第13期最强思维导图训练营已经结束一周了,但是我依旧是感觉所有学员还在努力的学习,这些学员中有教师、学生、白领、公务员、宝妈等等,只要你努力,只要你想改变自己,任何行业,任何岗位都可以参与进来,28天足以让你见成效,在这28天中,我们的学员不仅仅是收获了一枚毕业证,最重要的是让自己的思维方式得到升级,今天的你为自己投资,明天的你就会感谢你今天的付出,我们来听一听来自13期最强思维导图训练营优秀学员
基于CODESYS的多轴运动控制程序框架:逻辑与运动控制分离,快速开发灵活操作
GPJnCrbBdl
python开发语言
基于codesys开发的多轴运动控制程序框架,将逻辑与运动控制分离,将单轴控制封装成功能块,对该功能块的操作包含了所有的单轴控制(归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等)。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式,程序状态的跳转都已完成,只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义,能帮助开发者快速
C++ | Leetcode C++题解之第409题最长回文串
Ddddddd_158
经验分享C++Leetcode题解
题目:题解:classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
C++菜鸟教程 - 从入门到精通 第二节
DreamByte
c++
一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
java类加载顺序
3213213333332132
java
package com.demo;
/**
* @Description 类加载顺序
* @author FuJianyong
* 2015-2-6上午11:21:37
*/
public class ClassLoaderSequence {
String s1 = "成员属性";
static String s2 = "
Hibernate与mybitas的比较
BlueSkator
sqlHibernate框架ibatisorm
第一章 Hibernate与MyBatis
Hibernate 是当前最流行的O/R mapping框架,它出身于sf.net,现在已经成为Jboss的一部分。 Mybatis 是另外一种优秀的O/R mapping框架。目前属于apache的一个子项目。
MyBatis 参考资料官网:http:
php多维数组排序以及实际工作中的应用
dcj3sjt126com
PHPusortuasort
自定义排序函数返回false或负数意味着第一个参数应该排在第二个参数的前面, 正数或true反之, 0相等usort不保存键名uasort 键名会保存下来uksort 排序是对键名进行的
<!doctype html>
<html lang="en">
<head>
<meta charset="utf-8&q
DOM改变字体大小
周华华
前端
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
c3p0的配置
g21121
c3p0
c3p0是一个开源的JDBC连接池,它实现了数据源和JNDI绑定,支持JDBC3规范和JDBC2的标准扩展。c3p0的下载地址是:http://sourceforge.net/projects/c3p0/这里可以下载到c3p0最新版本。
以在spring中配置dataSource为例:
<!-- spring加载资源文件 -->
<bean name="prope
Java获取工程路径的几种方法
510888780
java
第一种:
File f = new File(this.getClass().getResource("/").getPath());
System.out.println(f);
结果:
C:\Documents%20and%20Settings\Administrator\workspace\projectName\bin
获取当前类的所在工程路径;
如果不加“
在类Unix系统下实现SSH免密码登录服务器
Harry642
免密ssh
1.客户机
(1)执行ssh-keygen -t rsa -C "
[email protected]"生成公钥,xxx为自定义大email地址
(2)执行scp ~/.ssh/id_rsa.pub root@xxxxxxxxx:/tmp将公钥拷贝到服务器上,xxx为服务器地址
(3)执行cat
在我们学习Java的过程中,掌握其中的基本概念对我们的学习无论是J2SE,J2EE,J2ME都是很重要的,J2SE是Java的基础,所以有必要对其中的基本概念做以归纳,以便大家在以后的学习过程中更好的理解java的精髓,在此我总结了30条基本的概念。 Java概述: 目前Java主要应用于中间件的开发(middleware)---处理客户机于服务器之间的通信技术,早期的实践证明,Java不适合
Memcached for windows 简单介绍
antlove
javaWebwindowscachememcached
1. 安装memcached server
a. 下载memcached-1.2.6-win32-bin.zip
b. 解压缩,dos 窗口切换到 memcached.exe所在目录,运行memcached.exe -d install
c.启动memcached Server,直接在dos窗口键入 net start "memcached Server&quo
数据库对象的视图和索引
百合不是茶
索引oeacle数据库视图
视图
视图是从一个表或视图导出的表,也可以是从多个表或视图导出的表。视图是一个虚表,数据库不对视图所对应的数据进行实际存储,只存储视图的定义,对视图的数据进行操作时,只能将字段定义为视图,不能将具体的数据定义为视图
为什么oracle需要视图;
&
Mockito(一) --入门篇
bijian1013
持续集成mockito单元测试
Mockito是一个针对Java的mocking框架,它与EasyMock和jMock很相似,但是通过在执行后校验什么已经被调用,它消除了对期望 行为(expectations)的需要。其它的mocking库需要你在执行前记录期望行为(expectations),而这导致了丑陋的初始化代码。
&nb
精通Oracle10编程SQL(5)SQL函数
bijian1013
oracle数据库plsql
/*
* SQL函数
*/
--数字函数
--ABS(n):返回数字n的绝对值
declare
v_abs number(6,2);
begin
v_abs:=abs(&no);
dbms_output.put_line('绝对值:'||v_abs);
end;
--ACOS(n):返回数字n的反余弦值,输入值的范围是-1~1,输出值的单位为弧度
【Log4j一】Log4j总体介绍
bit1129
log4j
Log4j组件:Logger、Appender、Layout
Log4j核心包含三个组件:logger、appender和layout。这三个组件协作提供日志功能:
日志的输出目标
日志的输出格式
日志的输出级别(是否抑制日志的输出)
logger继承特性
A logger is said to be an ancestor of anothe
Java IO笔记
白糖_
java
public static void main(String[] args) throws IOException {
//输入流
InputStream in = Test.class.getResourceAsStream("/test");
InputStreamReader isr = new InputStreamReader(in);
Bu
Docker 监控
ronin47
docker监控
目前项目内部署了docker,于是涉及到关于监控的事情,参考一些经典实例以及一些自己的想法,总结一下思路。 1、关于监控的内容 监控宿主机本身
监控宿主机本身还是比较简单的,同其他服务器监控类似,对cpu、network、io、disk等做通用的检查,这里不再细说。
额外的,因为是docker的
java-顺时针打印图形
bylijinnan
java
一个画图程序 要求打印出:
1.int i=5;
2.1 2 3 4 5
3.16 17 18 19 6
4.15 24 25 20 7
5.14 23 22 21 8
6.13 12 11 10 9
7.
8.int i=6
9.1 2 3 4 5 6
10.20 21 22 23 24 7
11.19
关于iReport汉化版强制使用英文的配置方法
Kai_Ge
iReport汉化英文版
对于那些具有强迫症的工程师来说,软件汉化固然好用,但是汉化不完整却极为头疼,本方法针对iReport汉化不完整的情况,强制使用英文版,方法如下:
在 iReport 安装路径下的 etc/ireport.conf 里增加红色部分启动参数,即可变为英文版。
# ${HOME} will be replaced by user home directory accordin
[并行计算]论宇宙的可计算性
comsci
并行计算
现在我们知道,一个涡旋系统具有并行计算能力.按照自然运动理论,这个系统也同时具有存储能力,同时具备计算和存储能力的系统,在某种条件下一般都会产生意识......
那么,这种概念让我们推论出一个结论
&nb
用OpenGL实现无限循环的coverflow
dai_lm
androidcoverflow
网上找了很久,都是用Gallery实现的,效果不是很满意,结果发现这个用OpenGL实现的,稍微修改了一下源码,实现了无限循环功能
源码地址:
https://github.com/jackfengji/glcoverflow
public class CoverFlowOpenGL extends GLSurfaceView implements
GLSurfaceV
JAVA数据计算的几个解决方案1
datamachine
javaHibernate计算
老大丢过来的软件跑了10天,摸到点门道,正好跟以前攒的私房有关联,整理存档。
-----------------------------华丽的分割线-------------------------------------
数据计算层是指介于数据存储和应用程序之间,负责计算数据存储层的数据,并将计算结果返回应用程序的层次。J
&nbs
简单的用户授权系统,利用给user表添加一个字段标识管理员的方式
dcj3sjt126com
yii
怎么创建一个简单的(非 RBAC)用户授权系统
通过查看论坛,我发现这是一个常见的问题,所以我决定写这篇文章。
本文只包括授权系统.假设你已经知道怎么创建身份验证系统(登录)。 数据库
首先在 user 表创建一个新的字段(integer 类型),字段名 'accessLevel',它定义了用户的访问权限 扩展 CWebUser 类
在配置文件(一般为 protecte
未选之路
dcj3sjt126com
诗
作者:罗伯特*费罗斯特
黄色的树林里分出两条路,
可惜我不能同时去涉足,
我在那路口久久伫立,
我向着一条路极目望去,
直到它消失在丛林深处.
但我却选了另外一条路,
它荒草萋萋,十分幽寂;
显得更诱人,更美丽,
虽然在这两条小路上,
都很少留下旅人的足迹.
那天清晨落叶满地,
两条路都未见脚印痕迹.
呵,留下一条路等改日再
Java处理15位身份证变18位
蕃薯耀
18位身份证变15位15位身份证变18位身份证转换
15位身份证变18位,18位身份证变15位
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 201
SpringMVC4零配置--应用上下文配置【AppConfig】
hanqunfeng
springmvc4
从spring3.0开始,Spring将JavaConfig整合到核心模块,普通的POJO只需要标注@Configuration注解,就可以成为spring配置类,并通过在方法上标注@Bean注解的方式注入bean。
Xml配置和Java类配置对比如下:
applicationContext-AppConfig.xml
<!-- 激活自动代理功能 参看:
Android中webview跟JAVASCRIPT中的交互
jackyrong
JavaScripthtmlandroid脚本
在android的应用程序中,可以直接调用webview中的javascript代码,而webview中的javascript代码,也可以去调用ANDROID应用程序(也就是JAVA部分的代码).下面举例说明之:
1 JAVASCRIPT脚本调用android程序
要在webview中,调用addJavascriptInterface(OBJ,int
8个最佳Web开发资源推荐
lampcy
编程Web程序员
Web开发对程序员来说是一项较为复杂的工作,程序员需要快速地满足用户需求。如今很多的在线资源可以给程序员提供帮助,比如指导手册、在线课程和一些参考资料,而且这些资源基本都是免费和适合初学者的。无论你是需要选择一门新的编程语言,或是了解最新的标准,还是需要从其他地方找到一些灵感,我们这里为你整理了一些很好的Web开发资源,帮助你更成功地进行Web开发。
这里列出10个最佳Web开发资源,它们都是受
架构师之面试------jdk的hashMap实现
nannan408
HashMap
1.前言。
如题。
2.详述。
(1)hashMap算法就是数组链表。数组存放的元素是键值对。jdk通过移位算法(其实也就是简单的加乘算法),如下代码来生成数组下标(生成后indexFor一下就成下标了)。
static int hash(int h)
{
h ^= (h >>> 20) ^ (h >>>
html禁止清除input文本输入缓存
Rainbow702
html缓存input输入框change
多数浏览器默认会缓存input的值,只有使用ctl+F5强制刷新的才可以清除缓存记录。
如果不想让浏览器缓存input的值,有2种方法:
方法一: 在不想使用缓存的input中添加 autocomplete="off";
<input type="text" autocomplete="off" n
POJO和JavaBean的区别和联系
tjmljw
POJOjava beans
POJO 和JavaBean是我们常见的两个关键字,一般容易混淆,POJO全称是Plain Ordinary Java Object / Pure Old Java Object,中文可以翻译成:普通Java类,具有一部分getter/setter方法的那种类就可以称作POJO,但是JavaBean则比 POJO复杂很多, Java Bean 是可复用的组件,对 Java Bean 并没有严格的规
java中单例的五种写法
liuxiaoling
java单例
/**
* 单例模式的五种写法:
* 1、懒汉
* 2、恶汉
* 3、静态内部类
* 4、枚举
* 5、双重校验锁
*/
/**
* 五、 双重校验锁,在当前的内存模型中无效
*/
class LockSingleton
{
private volatile static LockSingleton singleton;
pri