数据结构与算法系列第一篇——浅谈递归
数据结构与算法系列第一篇——浅谈递归
-
- 定义
-
- 举例
- 优点
- 递归使用注意事项
-
- 递归一定要有条件限定,保证能够停止下来,否则会发生栈溢出
- 在递归中虽然有限定条件,但是递归次数不能太多,否同也会发生栈内存溢出
- 构造方法禁止递归
- 案例分析
-
- 递归实现的二分查找算法
- 汉诺塔问题
- 归并排序
- 消除递归
-
- 递归和栈
- 总结
定义
在函数(方法)内部,可以调用其他函数。如果一个函数在内部调用自身本身,这就是递归调用,这个函数(方法)就是递归函数(方法)。
举例
阶乘n! = 1 x 2 x 3 x … x n,用函数fact(n)表示,可以看出:
fact(n) = n! = 1 x 2 x 3 x … x (n-1) x n = (n-1)! x n = fact(n-1) x n
所以,fact(n)可以表示为n x fact(n-1),只有n=0时需要特殊处理。0的阶乘为1
于是,fact(n)用递归的方式写出来就是:
package test;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int result = recursive(n);
System.out.println(result);
}
private static int recursive(int n) {
if(n==0){
return 1;
}else{
return recursive(n-1)*n;
}
}
}
优点
递归函数的优点是定义简单,逻辑清晰。理论上,所有的递归函数都可以写成循环的方式,但循环的逻辑不如递归清晰。
递归使用注意事项
递归一定要有条件限定,保证能够停止下来,否则会发生栈溢出
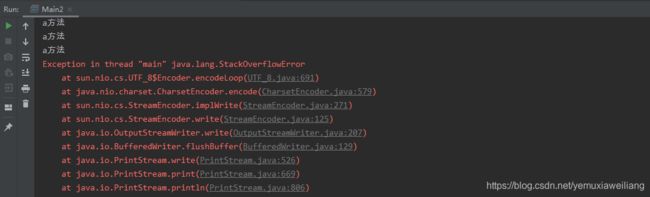
使用递归函数需要注意防止栈溢出。在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出。
package test;
public class Main2 {
public static void main(String[] args) {
a();
}
private static void a() {
System.out.println("a方法");
a();
}
}
在递归中虽然有限定条件,但是递归次数不能太多,否同也会发生栈内存溢出
构造方法禁止递归
案例分析
递归实现的二分查找算法
package test4;
public class OrdArray {
private long[] a;
private int elemSize;
public OrdArray(int max) {
a = new long[max];
elemSize = 0;
}
private int size() {
return elemSize;
}
public int find(long searchKey) {
return recFind(searchKey, 0, elemSize - 1);
}
/**
* 普通的二分查找
* @param searchKey
* @return
*/
public int binaryFind(long searchKey){
int lowerBound = 0;
int upperBound = elemSize - 1;
int curIndex;
while(true){
curIndex = (lowerBound + upperBound) / 2;
if(a[curIndex] == searchKey){
return curIndex;
}else if(lowerBound > upperBound){
return -1;
}else{
if(a[curIndex] < searchKey){
lowerBound = curIndex + 1;
}else{
upperBound = curIndex - 1;
}
}
}
}
/**
* 递归实现的二分查找算法
*/
private int recFind(long searchKey, int lowerBound, int upperBound) {
int curIndex;
curIndex = (lowerBound + upperBound) / 2;
if (a[curIndex] == searchKey) {
return curIndex;
} else if (lowerBound > upperBound) {
//找不到,返回
return -1;
} else {
if (a[curIndex] < searchKey) {
return recFind(searchKey, curIndex + 1, upperBound);
} else {
return recFind(searchKey, lowerBound, curIndex - 1);
}
}
}
/**
* 使用插入排序
* @param value
*/
public void insert(long value) {
int j;
for (j = 0; j < elemSize; j++) {
//找出在数组中已存在的数据比插入的数据小的数据,标记位置,返回数组索引值。
if (a[j] > value) {
break;
}
}
//将j(不包含)和elemSize(不包含)之间的索引位置的数据分别后移一位
for (int k = elemSize; k > j; k--) {
a[k] = a[k - 1];
}
//将数据插入在索引值的位置
a[j] = value;
elemSize++;
}
/**
* 数据展示
*/
public void display() {
for (int i = 0; i < elemSize; i++) {
System.out.print(a[i] + " ");
}
System.out.println("");
}
}
package test4;
public class BinarySearchApp {
public static void main(String[] args) {
OrdArray ordArray = new OrdArray(100);
ordArray.insert(72L);
ordArray.insert(90L);
ordArray.insert(45L);
ordArray.insert(126L);
ordArray.insert(54L);
ordArray.insert(99L);
ordArray.insert(144L);
ordArray.insert(27L);
ordArray.insert(135L);
ordArray.insert(81L);
ordArray.insert(18L);
ordArray.insert(108L);
ordArray.insert(9L);
ordArray.insert(117L);
ordArray.insert(63L);
ordArray.insert(36L);
ordArray.display();
long searchKey = 27L;
System.out.println("数字"+searchKey+"所在的位置:"+ordArray.find(searchKey));
searchKey = 54L;
System.out.println("数字"+searchKey+"所在的位置:"+ordArray.find(searchKey));
searchKey = 69L;
System.out.println("数字"+searchKey+"所在的位置:"+ordArray.find(searchKey));
System.out.println("===================");
searchKey = 27L;
System.out.println("数字"+searchKey+"所在的位置:"+ordArray.binaryFind(searchKey));
searchKey = 54L;
System.out.println("数字"+searchKey+"所在的位置:"+ordArray.binaryFind(searchKey));
searchKey = 69L;
System.out.println("数字"+searchKey+"所在的位置:"+ordArray.binaryFind(searchKey));
}
}
运行结果如下图:
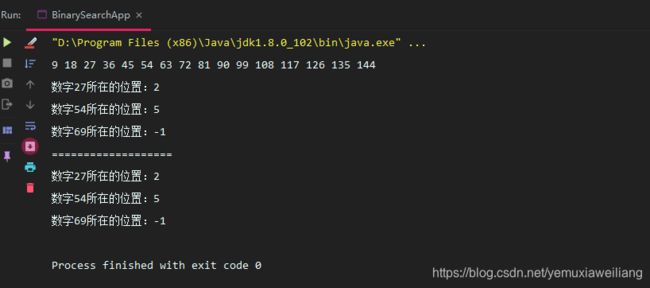
递归的二分查找和非递归的二分查找算法的时间复杂度都是O(logN)。递归的二分查找代码更简洁一些,但是它的效率可能会慢一些。
递归的二分查找算法是分治算法的一个例子。把一个大问题划分成两个相对来说更小的问题,并且分别解决每个小问题。对每一个小问题的解决方法是一样的;把每个小问题分成两个更小的问题,并且解决它们,这个过程一直持续下去直到达到易于求解的基值情况,就不用再继续分了。
汉诺塔问题
问题描述:有若干盘子(所有盘子直径不同),盘子中间有洞,可以放置在塔座上。总共三个塔座A,B,C;所有盘子开始放置在塔座A上(直径由大到小依次叠放)。
实现目标:将所有盘子移动到塔座C上。
注意事项:每一次只能移动一个盘子,且任何盘子都不可以放置在比自己小的盘子下面。
问题解析:塔座A上的盘子是初始的金字塔形排列是一棵树(非数据结构中的树)。盘子数小于盘子总数的较小的树称为子树。生成盘子较小的树形堆是问题解决过程中的第一步。
举例来说,如果要移动4个盘子,会发现中间的一个状态是有3个盘子的子树在塔座B上。

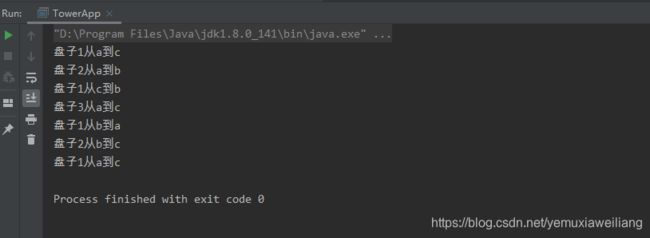
package test3;
public class TowerApp {
public static void main(String[] args) {
//模拟三个盘子
int disks = 3;
//a,b,c为三个塔座
doTower(disks, 'a', 'b', 'c');
}
/**
* 汉诺塔算法
*
* @param disks 盘子数
* @param from 源地址
* @param inter 中间地址
* @param to 目的地址
*/
private static void doTower(int disks, char from, char inter, char to) {
if (disks == 1) {
System.out.println("盘子" + disks + "从" + from + "到" + to);
} else {
doTower(disks - 1, from, to, inter);
System.out.println("盘子" + disks + "从" + from + "到" + to);
doTower(disks - 1, inter, from, to);
}
}
}
归并排序
归并排序的思想:把一个数组分成两半,排序每一半,然后用merge()方法把数组的两半归并成一个有序的数组。使用递归为每一半排序,再进行merge()。反复的分割数组,直到得到的子数组只含有一个数据项,设定只有一个数据项的数组是有序的(基值条件)
package test4;
public class DArray {
private long[] theArray;
private int arraySize;
public DArray(int max) {
theArray = new long[max];
arraySize = 0;
}
public void insert(long value){
theArray[arraySize] = value;
arraySize++;
}
public void display() {
for (int i = 0; i < arraySize; i++) {
System.out.print(theArray[i] + " ");
}
System.out.println("");
}
public void mergeSort(){
//重点:归并排序需要和原始数组一样大小的临时数组空间
long[] workSpace = new long[arraySize];
recMergeSort(workSpace,0,arraySize-1);
}
private void recMergeSort(long[] workSpace, int lowerBound, int upperBound) {
if(lowerBound == upperBound){
return;
}else{
int mid = (lowerBound+upperBound)/2;
recMergeSort(workSpace,lowerBound,mid);
recMergeSort(workSpace,mid+1,upperBound);
merge(workSpace,lowerBound,mid+1,upperBound);
}
}
private void merge(long[] workSpace, int lowPtr, int highPtr, int upperBound) {
int j = 0;
int lowerBound = lowPtr;
int mid = highPtr - 1;
int n= upperBound-lowerBound+1;
while (lowPtr<=mid && highPtr<= upperBound){
if(theArray[lowPtr]<theArray[highPtr]){
workSpace[j++] = theArray[lowPtr++];
}else{
workSpace[j++] = theArray[highPtr++];
}
}
while (lowPtr<=mid){
workSpace[j++] = theArray[lowPtr++];
}
while (highPtr<=upperBound){
workSpace[j++] = theArray[highPtr++];
}
for (j = 0; j < n; j++) {
theArray[lowerBound+j] = workSpace[j];
}
}
}
package test4;
public class MergeSortApp {
public static void main(String[] args) {
DArray array = new DArray(100);
array.insert(64);
array.insert(21);
array.insert(33);
array.insert(70);
array.insert(12);
array.insert(85);
array.insert(44);
array.insert(3);
array.insert(99);
array.insert(0);
array.insert(108);
array.insert(36);
array.display();
array.mergeSort();
array.display();
}
}
消除递归
递归和栈
递归和栈之间有一种紧密的联系,事实上,大部分的编译器都是使用栈来实现递归的。当调用一个方法的时候,编译器会把这个方法的所有参数及其返回地址都压入栈中,然后把控制转移给这个方法。当这个方法返回的时候,这些值退栈。参数消失了,并且控制权重新回到返回地址处。
再次理一下头绪:
- 当一个方法被调用时,它的参数以及返回地址被压入栈中
- 这个方法可以通过获取栈顶元素的值来访问它的参数
- 当这个方法要返回的时候,他查看栈以获得返回地址,然后这个地址以及方法的所有参数退栈,并且销毁
案例:
求n的前n项和
package test2;
public class StackX {
private int maxSize;
private int[] stackArray;
private int top;
public StackX(int maxSize) {
this.maxSize = maxSize;
stackArray = new int[maxSize];
top = -1;
}
public void push(int p){
stackArray[++top] = p;
}
public int pop(){
return stackArray[top--];
}
public int peek(){
return stackArray[top];
}
public boolean isEmpty(){
return top == -1;
}
}
package test2;
public class StackTriangleApp {
private int theNumber;
private int theAnswer;
private StackX theStack;
public StackTriangleApp(int theNumber, int theAnswer, StackX theStack) {
this.theNumber = theNumber;
this.theAnswer = theAnswer;
this.theStack = theStack;
}
public void stackTriangle() {
while (theNumber>0){
theStack.push(theNumber);
--theNumber;
}
while (!theStack.isEmpty()){
int newN = theStack.pop();
theAnswer+=newN;
}
}
public int getTheAnswer() {
return theAnswer;
}
}
package test2;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
System.out.println("输入一个数:");
Scanner scanner = new Scanner(System.in);
int theNumber = scanner.nextInt();
StackX stackX = new StackX(1000);
int theAnswer = 0;
StackTriangleApp app = new StackTriangleApp(theNumber,theAnswer,stackX);
app.stackTriangle();
System.out.println(app.getTheAnswer());
}
}
总结
- 一个递归的方法每次用不同的参数值反复调用自身。
- 某种参数值使递归的方法返回,而不再调用自身,这称为基值情况。
- 当递归方法返回时,递归过程通过逐渐完成各层方法实例的未执行部分,而从最内层返回到最外层的原始调用处。
- 汉诺塔问题包含三个塔座和任意数量的盘子
- 汉诺塔可以使用递归解决,它的思想是:把除了最底层盘子外的所有盘子形成的子树移动到一个中介塔座上,然后把最底层的盘子移到目标塔座上,最终把那个子树移动到目标塔座上。
- 归并排序的效率为O(N*logN)
- 归并排序需要一个大小等于原来数组的工作空间。
- 对于阶乘以及二分查找,它们递归的方法只包含一次对自身的调用,(在二分查找代码显示了两次,但是运行只有一次自身的调用执行);
- 汉诺塔和归并排序问题,它们的递归包含两次递归调用。
- 任何可以用递归完成的操作都可以用一个栈来实现。
- 递归的方法可能效率低,有时候可以用一个简单循环或者是一个基于栈的方法来替代它。