基于相移法的结构光三维测量技术

1. 结构光三维测量原理

1.1 单目结构光系统

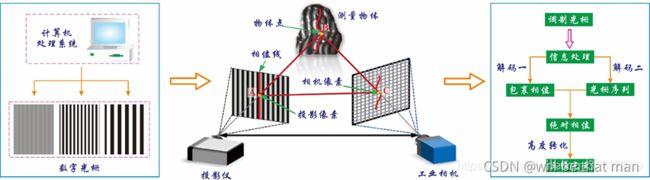
结构光投影三维测量系统主要由一个CCD相机、投影仪和PC机组成，如图所示。首先在PC上进行结构光编码，通过投影仪将编码好的结构光投影至物体表面，再由数字相机拍摄受物体表面调制的结构光图像，图像最后传至PC进行解码，将解码信息还原成物体的三维高度信息。下图给出条纹结构光的系统图。

1.2 结构光投影三维测量原理

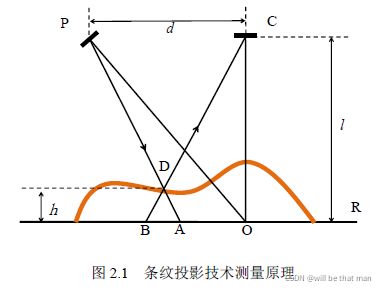
计算机编码的一系列正弦条纹图案经投影仪 P 投射到被测物体表面上，条纹图经物体表面调制后携带深度信息，相机 C 采集得到一系列变形条纹图。图中，D 为被测物体表面上一点，投射到D点的一束光线为 PD，将其延长刚好交参考平面 R 于点 A 。光线 DC 为相机接收到的 D 点的反射光线，将其反向延长刚好交参考平面与点 B 。由于编码图案为正弦条纹图，同一条投射光线上的相位值相等，即 D 和 A 点的相位值相等。同样的，相机采集到的反射光线 DC 上，D 点的相位和 B 点的相位相等。因此，参考平面上 A 点与 B 点间的相位差与变形条纹上的 D 点的深度有关。

以上这些公式好像只是一个去除了量纲的理论模型，不太准确，只是为了说明相位差和高度有关，后面再回来看

2. 相移法概述

结构光主要研究其编解码的方法，按照编码的方式来划分的话，结构光可以分为时序编码、空间编码和直接编码，其中时序编码和空间编码都拥有其各自的优点，而受到广泛的使用。其中时序编码中的相移法由于其算法简单，精度高，得到广泛的研究与应用。因此，本文主要针对时序编码中的相移法进行讲解，相移法也叫相位测量轮廓术（PMP）。

相移法主要是通过投影多幅具有相位差的结构光图像来获得相位信息，常见的几种算法有三步相移法、四步相移法和五步相移法。传统相移法中条纹光栅的投影往往通过机械移动来实现相移，这大大降低了测量精度，近些年由于DLP等投影技术的发展，相移可以通过PC机编程结合DLP投影的方式实现准确相移，测量精度较传统方法有了很大的提高。

2.1 相移法存在的问题

相移法存在一些问题：

• 投影的非线性问题
• 包裹相位展开问题
• 相位误差补偿问题

2.1.1 投影的非线性问题

投影仪普遍存在Gamma非线性关系，正弦结构光图案经过投影并由相机拍摄后，获得的图像并不具备良好的正弦性。在三维测量的过程中，直接使用这种未经矫正的图案会导致相位误差。因此，系统需要对投影仪进行精确的非线性矫正才能得到良好的三维重建效果。

2.1.2 包裹相位展开

在相移法中，包裹相位（也叫折叠相位）的获取是通过四象限反正切函数获得的，相位局限在[-π，π]范围内，最终的绝对相位需要通过相位展开或相位解包裹的方式获得。由于环境光、噪声、阴影等因素的影响，很容易造成相位展开的错误。因此，如何准确的进行包裹相位的展开成为提高三维测量精度的一个难点。目前求解绝对相位有很多成熟的方法：

• 格雷码法
• 多频外差法
• 倍频法
• phase-coding法
• …

将相位转化为三维点云也有很多经典的方法，例如（1）相位差法（2）东南大学达飞鹏老师的8参数方法（3）反向相机方法。后两种方法最为灵活，应用相对也更为广泛。

2.1.3 相位误差补偿

传统相移法主要通过机械移动的方式实现相位移动，而由于机械装置的精度关系，经相机拍摄得到的相移图像 经过图像处理后，得到的包裹相位图往往带有带有很大的相位误差，从而造成测量精度的降低。而随着DLP投影技术和PC技术的发展，现在可以利用编程实现图像的精确相移，大大减小了因为相移带来的相位误差。现在的相位误差主要由投影仪的非线性造成。

2.2 相移法原理

相移法主要是通过投影多幅具有相位差的结构光图像来获得相位信息。对于常见的等相移步距的 N 步相移法，其第$n(n=1,2,3...N)$幅投影正弦结构光图像的灰度值$I_n(x,y)$分布可以表示为：

$$I_n(x,y)=B(x,y)+A(x,y)cos[\varphi (x,y)+2\pi n/N]$$

式中，$B(x,y)$是背景光强，$A(x,y)$是强度调制参量，$\varphi (x,y)$为相位编码值。当然，也可以采用非等相移步距的多步相移法。式中，我们关注的是相位主值$\varphi (x,y)$，因为它对每个每个像素点是唯一的，可以通过下式求得：

上式中含有三个未知数，分别是$\varphi (x,y)$，$B(x,y)$，$A(x,y)$，要求出$\varphi (x,y)$，至少需要3个方程，也就是说至少需要三张相移图片。常用的相移步数有3步和4步，一般来说，相移步数越少，效率越高；相移步数越多，越能减少因光照不均匀而产生的相位偏差而提高测量精度；但大步数的相移法意味着更多的投影图像，更长的计算时间。因而在实际情况中，往往根据不同的三维测量需要而选择合适的相移步数。

（1）三步相移法

三步相移法只需投影三幅相移结构光图案，其常用的等步距相移增量为$2\pi /3$，当然也可以为其他任意值。根据式2.7，可得：

三步相移法另一种相移增量为$\pi /2$。

（2）四步相移法
四步相移是最常用的一种相移法，相移法步距常常选为$\pi /2$。因为四步相移对称性关系，相比三步相移法，能有效减小对称性的相位误差。根据式2.7可得包裹相位：

3 相位展开原理

在相移法中，由式2.8可知，相位$\varphi (x,y)$是通过四象限反正切函数获得的，一般将该相位定义为包裹相位（Wrapped phase），其值域在$[-\pi ,\pi ]$内。因此从，如果采用大于一个周期的条纹图像进行解码，求得的将是不连续的包裹相位，如图所示，最终连续的绝对相位需要进行相位展开（Phase unwrapping）获得。

以一维相位展开为例，包裹相位和绝对相位的关系如下所示：

式中，${\varphi }_w(k)$为坐标k点的包裹相位值，${\varphi }_a(k)$为坐标点k的绝对相位值，$n_k$为坐标k点对应的条纹级次。相位展开的精度取决于相位级次的准确性。传统方法一般采用邻域分析法进行相位展开，即只分析相邻像素的相位差值。若相邻两个像素的相位差值的绝对值大于$\pi$，说明两个像素不在一个周期内，若前一个像素对应级次为n，后一个像素的级次则为n+1：

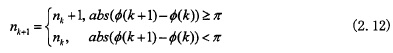
将一维的相位扩展到二维，就可以对政府包裹相位图进行相位展开，从而得到连续的绝对相位值。在实际情况下，由于背景噪声，非线性等因素影响，传统邻域分析法进行相位展开方式已经逐渐不适用。由式2.12可知，加入某一点相位展开错误，则它周围点通过该点进行相位展开时也是错误的，继续通过邻域分析法进行相位展开的话，会导致接下来所有像素点都展开错误，这就是所谓的相位误差的累加效应

相位展开总体来说可以分成空域相位展开和时域相位展开。

这里先给出空域展开和时域展开的区别：

• 空域展开：依靠空间相邻像素点之间的相位值恢复绝对相位，如果重建表面不连续，则出现解码错误，且往往会受到阴影、噪声的影响。
• 时域展开：将每个像素点的相位值进行独立计算，有格雷码和多频外差两种，其中格雷码方法对物理表面问题敏感，并且多投影的图并不能用来提升精度，多频外差精度更高。

当然目前还有更多精度更高、效率更快的相位展开方法，在这里暂时不予讨论。

3.1 空域相位展开

• 空域展开：依靠空间相邻像素点之间的相位值恢复绝对相位，如果重建表面不连续，则出现解码错误，且往往会受到阴影、噪声的影响。

3.2 时域相位展开

时域相位展开是基于时间序列，在一段连续的时间序列内投影一系列结构光图案值被测物体表面，并由相机同步拍摄变形图像，最终每个像素点的绝对相位通过这些以时间为序列的图案独立计算得出，因而可以避免相位误差的叠加。时域展开公式如下：

其中，$k(x,y)$为像素点$(x,y)$对应的相位级次。

相比于空域展开算法，由于时域展开中每个点的相位是独立计算的，避免了相位误差叠加的影响，因而该方法更适合测量一些表面不连续、阶跃型的物体场景，且不受其物体表面形貌的影响。时域展开主要有基于相移法-格雷码编码算法和多频外差法。

3.2.1 相移-格雷码编码法

相移-格雷码编码相位展开的原理是先将格雷码转化成二进制码，接着进行逻辑异或运算，再将码值转化成十进制数。格雷码转化成二进制码如下图所示：

对应包裹相位的级次k可通过二进制码计算得出：

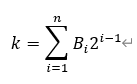
各个像素点的级次确定后，就可以确定绝对相位了。

格雷码相位展开的过程如下图所示，其中蓝线是包裹相位，红线是相位级次，黄线是绝对相位，也叫展开相位。

3.2.2 多频外差法

多频外差原理是通过多个不同频率（周期）的正弦光栅的相位做差，将小周期的相位主值转化为大周期的相位差，从而使得相位差信号覆盖整个视场，然后再根据相位差来得到整幅图像的绝对相位分布。

双频外差

这里以双频外差为例，原理如图所示：

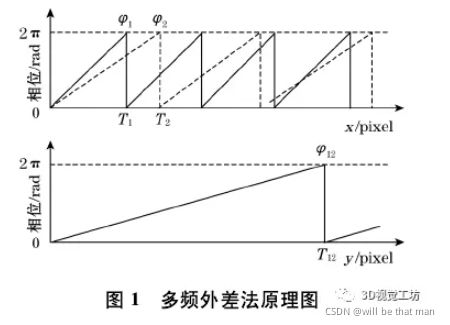
注：通常我们说的相位函数的周期，代表的是一个周期正弦函数所占的像素单位的个数

多频外差

在使用三频外差后，相位差信号的周期大于整幅图像，也就是说，图像中每个像素在这个周期内都有唯一的相位，这个就是绝对相位。

代码实践

依据相移法得到的包裹相位图如下图所示，不同颜色代表不同频率的相位主值：

我们用三频外差后的效果：

在这里，我们可以看到，三个周期小的相位可以合成一个周期更大的编码图案。

明白了原理，我们来代码实践一下，需要注意的是，求解出来的相位我们要进行归一化到区间操作：

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号


def phase_simulation(WIDTH, T1, T2, T3):
    # 创建长度为WIDTH，周期为T1，T2，T3的三个正弦函数
    pha1,pha2,pha3 = np.zeros(shape=WIDTH),np.zeros(shape=WIDTH),np.zeros(shape=WIDTH)
    t1,t2,t3 = 1,1,1
    for idx in range(WIDTH):
        # pha1
        if(t1 > T1):
            t1 = 1
        pha1[idx] = (t1/T1)*2*np.pi
        # pha2
        if (t2 > T2):
            t2 = 1
        pha2[idx] = (t2 / T2) * 2 * np.pi
        # pha3
        if (t3 > T3):
            t3 = 1
        pha3[idx] = (t3 / T3) * 2 * np.pi
        # t1,t2,t3自增
        t1 += 1
        t2 += 1
        t3 += 1
    return pha1,pha2,pha3


def parse_phase(pha1, pha2, T1, T2):
    # 创建pha12，作为双频外差的相位
    pha12 = np.zeros_like(pha1)
    # 计算两个相位的差
    pha12 = np.where(pha1 > pha2, pha1 - pha2, pha1 - pha2 + 2 * np.pi)
    # 计算双频外差的周期T12
    T12 = T1 * T2 / (T2 - T1)
    # 计算双频外差
    # 方法1
    pha12 = T2 / (T2 - T1) * pha12
    # 方法2
    # m = np.round((T2 / (T2 - T1) * pha12 - pha1) / (2 * np.pi))
    # pha12 = 2 * np.pi * m + pha12

    # 归一化到[0,2pi]
    min_value, max_value = np.min(pha12),np.max(pha12)
    pha12 = (pha12 - min_value) / (max_value - min_value) * 2 * np.pi
    return pha12,T12



if __name__ == '__main__':
    # 视场宽度
    WIDTH = 854
    # 条纹周期
    T1 = 11
    T2 = 12
    T3 = 13

    # 模拟宽度为Width的正弦图像，正弦函数的周期为T1，T2，T3
    pha1,pha2,pha3 = phase_simulation(WIDTH,T1,T2,T3)
    # 画图
    X = np.arange(0,WIDTH)
    plt.plot(X,pha1,label='pha1')
    plt.plot(X, pha2, label='pha2')
    plt.plot(X, pha3, label='pha3')
    plt.title('相移主值图（仿真）')
    plt.xlabel('像素')
    plt.ylabel('w/rad')
    plt.legend()
    plt.show()

    # 解相位
    pha12, T12 = parse_phase(pha1,pha2,T1,T2)
    pha23, T23 = parse_phase(pha2, pha3, T2, T3)
    pha123, T123 = parse_phase(pha12, pha23, T12, T23)

    # 画图
    plt.plot(X, pha12, label='pha12')
    plt.plot(X, pha23, label='pha23')
    plt.plot(X, pha123, label='pha123')
    plt.title('解出绝对相位')
    plt.xlabel('像素')
    plt.ylabel('w/rad')
    plt.legend()
    plt.show()

4. 投影的非线性校正

上文说到，投影仪存在Gamma非线性，正弦光栅编码在经过投影仪和相机拍摄后，真正获得的条纹并不是正弦条纹。下面给出实际光栅的表达式，当输入为一个线性函数时，其输出（相机拍摄）是一个非线性的函数：

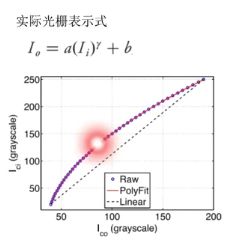
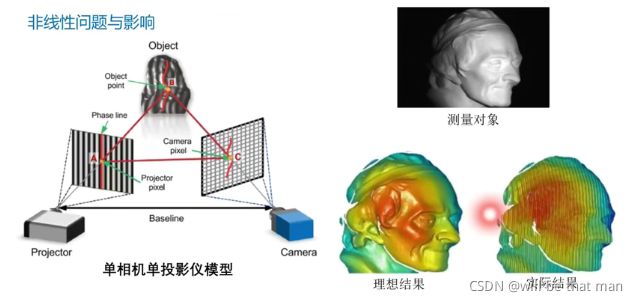
下图是用三步相移法获得的测量对象的三维重建结果，可以看到，实际结果相比于理想结果，表面出现了许多水波纹，其原因就是投影仪的非线性。当然，这个例子是投影仪非线性比较严重的。因此，正弦条纹经投影仪投影后，由相机拍摄得到的结构光图像不具有良好的正弦性。直接使用这些未经校正的图案的话，会造成包裹相位展开错误。

结构光三维测量系统往往要对整个测量系统进行非线性校正才能获得较好的三维重建效果，但高精度的校正往往比较复杂、且不一定适用于所有测量系统。因此不受非线性影响（避免非线性影响）的结构光三维测量方法称为研究的热点，为此国内外学者对此进行了广泛而深入的研究，并提出了多种方法。最常见的就是二值条纹离焦、双目结构光的方法。

4.1 二值条纹离焦及其优化算法

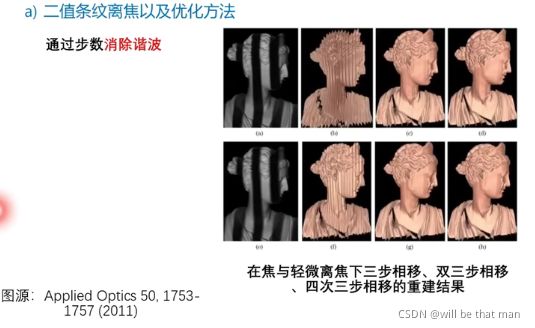
二值条纹只有两个灰度级，及时受到非线性的变换，其结果也还是二值条纹，因此二值条纹不会受非线性的影响而改变形状。在数字信号处理中，方波信号（二值条纹）可以通过傅里叶变换分解成多个正弦信号的叠加，通过滤波器将高频谐波信号滤掉，可以得到良好的正弦波信号。受此启发，我们可以通过离焦投影系统将二值条纹离焦成正弦条纹，从而避免投影非线性的影响。下图是二值条纹通过不同离焦核获得的正弦光栅信号：

上图可以看到，离焦会导致条纹的调制度（对比度）下降，对比度越低，意味着相位的质量越低。所以需要对算法进行优化，以提高相位质量，常见的方法有两种：

1. 通过增加相移步数消除谐波，如下图所示：注：步数增加会提高计算复杂度
   
2. 通过算法调制用更小的离焦核形成正弦，如下图所示：
   

离焦投影系统

经过Floyd-Steinberg抖动算法处理的正弦条纹离焦

图像抖动是一种广泛应用于图像印刷领域的技术。它用0和255两种灰度来近似显示具有更多灰度级的灰度图像。其中基于Floyd-Steinberg的图像抖动技术应用最为广泛。已有的研究证明，经抖动算法处理后的正弦条纹通过离焦投影系统可以得到高质量的正弦条纹图案。

关于Floyd-Steinberg抖动算法，小弟的另一篇博客DITHER抖动算法对其进行了详细讲解。

在一篇硕士论文基于自适应结构光投影的三维测量系统研究（小弟的这篇博客也大多参考自这篇文章）中，作者对Floyd-Steinberg抖动算法进行了研究，分析它对正弦图案进行处理并用于离焦系统，然后产生高质量的正弦图像，用于结构光相移法三维重建。分析的结果是：

• 该算法的误差扩散不对称性将使正弦结构光图案的二值图案失去对称性，对相移法将产生相位平移的影响。
• 同时该算法对正弦条纹方向具有选择性，使用平行于条纹方向扫描的抖动算法将使离焦投影的正弦条纹图案在不同 离焦状态、不同相移步数情况下的相位提取结果更加一致、误差更小。

4.2 双目结构光方法

使用双目立体匹配的方法，无需相位的解码，如下图：

对于投影非线性矫正的一些算法，下面给出一些参考文献：

参考文献

[1]熊义可. 基于自适应结构光投影的三维测量系统研究[D]. 浙江大学, 2016.