Java的函数一一方法（含汉诺塔问题）

个人主页：Ice_Sugar_7
所属专栏：快来卷Java啦

方法的概念

Java的方法和C语言的函数差不多，这里只讲一些有区别的地方。我们以一个简单的求和函数为例：

public class Method{
// 方法的定义
	public static int add(int x, int y) {
		return x + y;
	}
}

①首先public static是修饰符，现阶段直接使用 public static 固定搭配。
②然后是参数列表，如果方法没有参数，那么（）里面什么都不用写。
③方法必须写在类当中，也就是说你不能在类外面凭空定义一个方法。
④方法不能嵌套定义，一个方法里面不能再定义另外一个方法。

有一点要单独拿出来说：⑤在java当中，没有方法声明这一说。方法是不用声明的。
C语言编译代码时是自上向下编译的，如果你在上面写了A函数，下面写了B函数，那A是不认识B的，你要在A函数中调用B函数，就得进行声明；
而Java编译是看全局的，还是上面那个例子，在Java当中A是认识B的，所以这回你不用声明，直接调用B。

方法的重载

有这样的一个情境：

你写了一个求两个整数之和的方法，但如果你想求三个数的和、四个数的和…乃至n个数之和，甚至你要求n个浮点数之和，那岂不是每一次都要重新写一个方法？！麻烦死了！
所以方法重载应运而生。

所谓的重载，简单理解就是“一词多义”：比如“好人”一词，可以指一个人品行端正良好，而当下互联网中衍生出的“好人卡”一词中的好人则是另外一个意思。（懂的都懂，希望你们不会被发好人卡）
所以当我们把“一词多义”代入到Java的语境之中，就是指方法名相同，但是参数列表不同。
参数列表指的是参数的个数、参数的类型、类型的次序，在方法名相同的情况下，这三个只要有一个不同，那么这个方法就会被重载了。
不知道你有没有发现，参数列表是不包括返回值类型的，这是一个要注意的点：两个方法如果仅仅只是因为返回值类型不同，是不能构成重载的。（你这样写的话编译器会报错的。）

方法签名

看到这里你肯定会有疑问：在同一个作用域中不能定义两个相同名称的标识符。比如：方法中不能定义两个名字一样的变量，那为什么类中就可以定义方法名相同的方法呢？

这就与方法签名有关了，方法签名即：经过编译器编译修改过之后方法最终的名字。它的具体方式为：方法全路径名+参数列表+返回值类型，构成方法完整的名字。方法名并不是我们表面所看到的“add”。
有这样的一段代码：

public class TestMethod {
	public static int add(int x, int y){
		return x + y;
	}
	public static double add(double x, double y){
		return x + y;
	}
	public static void main(String[] args) {
		add(1,2);
		add(1.5, 2.5);
	}
}

上述代码经过编译之后，然后使用JDK自带的javap反汇编工具查看，具体操作如下：

1. 先对工程进行编译生成.class字节码文件
2. 在控制台中进入到要查看的.class所在的目录
3. 输入：javap -v 字节码文件名字即可
   
   注：D指的就是double，I就是int。

---

递归

假如当下有一个问题，我们可以把它拆成一个小的问题，而这个小的问题又可以拆成更小的问题，并且这些问题的解决办法相同，那我们就可以使用递归，它类似数学中的数学归纳法，你想一下，数学归纳法需要你找到某个规律，然后证明第一项符合这个规律和每项之间的递推关系，这个递推关系指的是假如第k项成立，你就可以推出第（k+1）项也成立，上述这两个条件成立的话，那你就可以推出第一项到第n项都符合这个规律。而递归要你找到从第n项往前推的方法。
所以，递归的出口其实是数学归纳法的起始（第一项）。

在递归之中，方法的调用是需要开辟内存的，而当它调用结束后，这块内存就销毁了。而如果一直调用但是不“归”，会导致栈溢出，因此递归需要有一个出口，

例题：汉诺塔问题

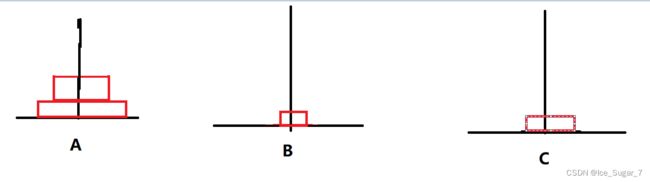
首先我们来分析一下四个盘子的情况

首先把最上面盘子放到B柱，第二个盘子放在C柱；

然后把第一个盘子放到第二个盘子上面，再把第三个盘子放到B柱；

再把第一个盘子先放A柱（第四个盘子上面），然后第二个放第三个上面，再将第一个放第二个上面，得到上图。
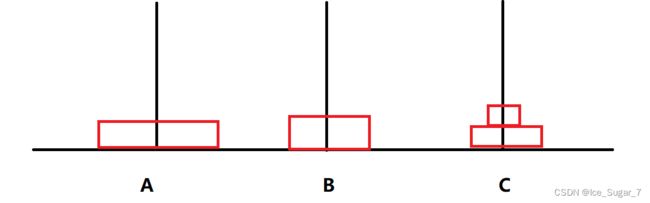
接着将第四个放C柱

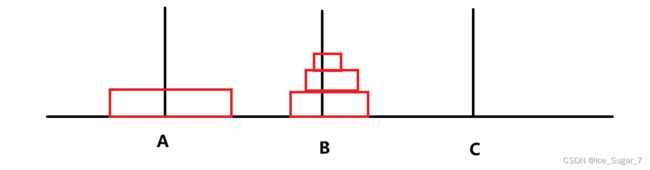
最开始n个盘子在A柱，那我就得先把上面的（n-1）个盘子移到B，这个移动过程我们得借助C才能移到B。移好之后就得考虑把（n-1）个盘子移到C，那我们继续拆分问题，就是把上面的（n-2）个盘子先借助C移动到A，这样B柱就只剩下一个盘子，把它移动到C就ok了。
现在剩下（n-2）个盘子在A柱，仿照上面的思路，先把（n-3）个盘子借助C移到B，再把A柱剩下的一个盘子拿到C，剩下（n-3）个盘子重复上面的做法。
至此，你应该找到递归的感觉吧？那接下来开始写代码。

首先来写一个方法，它用来记录每次移动一个盘子的轨迹（把这个盘子从哪移到哪，就是下面的pos1和pos2）

   public static void move(char pos1,char pos2) {
       System.out.print(pos1 + "->" + pos2 + ' ');  //打印移动途径
   }

接着我们来写移动盘子的方法，它应该有四个参数：盘子数，移动前所处的柱子，移动时要借助的柱子（称为中转柱），要移动到的柱子。

   public static void hanio(int n,char pos1,char pos2,char pos3) {
       if(n == 1) {
           move(pos1,pos3);   //只有一个盘子时就直接移到C柱
           return;
       }
       else {
           hanio(n-1,pos1,pos3,pos2);
           move(pos1,pos2);
           hanio(n-1,pos2,pos1,pos3);
       }
   }

我们将A、B、C分别记为pos1，pos2，pos3（注意与上面函数的pos1，pos2，pos3作区分），然后来写下main函数：

    public static void main(String[] args) {
        char pos1 = 'A',pos2 = 'B',pos3 = 'C';
        hanio(5,pos1,pos2,pos3);
    }

这里我们来试下四个盘子时的移动情况

那么在解决了这个问题之后，我们来思考一下从中学到了什么，或者说对递归有无更深的理解。

递归采用的就是“大事化小”的思路，比如上面我们要移动n个盘子，那么就把这个问题转化为移动（n-1）+1 个盘子，而移动（n-1）个盘子又可以转化为移动（n-2）+1个盘子。
这道题的难点在于，它表面要你把最底下的盘子移过去，但实际上你要关注的是它上面的（n-1）个盘子，然后你要知道这（n-1）个盘子每一次移动的方法都是“借助C柱，在A和B之间来回移动”，假如某次移动后（n-1）个盘子在A，那原先最底下那个盘子就在B，此时直接把它拿到C就ok了