二叉树OJ
文章目录
- 根据二叉树创建字符串
- 二叉树层序遍历
- 二叉树的最近公共祖先
- 从前序与中序遍历序列构造二叉树
- 二叉搜索树与双向链表
正文开始前给大家推荐个网站,前些天发现了一个巨牛的 人工智能学习网站, 通俗易懂,风趣幽默,忍不住分享一下给大家。 点击跳转到网站。
根据二叉树创建字符串
示例
这个题的本质就是一个前序遍历,只不过遍历完根以后再遍历左子树和右子树是都需要用一对括号将他们扩起来,每颗子树同理,只不过如果右子树不存在,右子树的括号就可以省略,但是只要右子树存在,左子树的括号就不可以省略,不然会破坏对应关系。
总结:
所以进行左路递归的条件就是左子树存在或者右子树存在,因为这两种情况左子树都需要加括号,右子树递归的条件很简单,就是右子树存在就可以了。
解题代码:
class Solution {
public:
string tree2str(TreeNode* root)
{
//用string来链接字符串
string str;
if(root==nullptr)
{
return str;
}
//将数字转化为字符串
str+=to_string(root->val);
if(root->left||root->right)
{
str+="(";
str+=tree2str(root->left);
str+=")";
}
if(root->right)
{
str+="(";
str+=tree2str(root->right);
str+=")";
}
return str;
}
};
二叉树层序遍历
题目
层序遍历可以理解为广度优先遍历,就是一层一层的遍历,这个思路其实也挺简单的,我们可以用一个队列把根放进去,然后出根的同时把左子树和右子树放进去,但是有一个问题,我们需要把每一层的数据放到一个vector中去,但是我们没办法控制,所以我们还需要一个变量来控制每一层数据的个数,来达到这个目的。
解题代码:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
queue<TreeNode*> q;
//根不为空就入队
if(root)
q.push(root);
//第一层默认为一个值
int leval = 1;
vector<vector<int>> vv;
//队列不为空就说明还有数据没遍历到
while(!q.empty())
{
vector<int> v;
while(leval--)
{
TreeNode* front = q.front();
//保存每个数据
v.push_back(front->val);
q.pop();
//不为空就入队
if(front->left)
{
q.push(front->left);
}
//不为空就入队
if(front->right)
{
q.push(front->right);
}
}
// 把每层的数据保存起来
vv.push_back(v);
//一层结束后,队列中元素的个数就是下一层的数据的个数
leval = q.size();
}
return vv;
}
};
二叉树的最近公共祖先
思路一:
直接暴力求解,我们遍历二叉树,遍历的同时在左边找p,如果p在左边那么p就一定不在右边,用同样的方式找q,都找完以后,如果一个在左边一个在右边,那说明该节点就是公共祖先,如果两个节点都在左边,我们就去左边找公共祖先,还是同样的方法,如果在右边就去右边找。
解题代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool Find(TreeNode* root, TreeNode* x)
{
if(root==nullptr)
{
return false;
}
if(root==x)
{
return true;
}
return Find(root->left,x)||Find(root->right,x);
}
TreeNode* _lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
if(root==q||root==p)
{
return root;
}
bool pInleft = Find(root->left,p);
//左边没有就一定在右边,左边有就一定不在左边
bool pInright = !pInleft;
bool qInleft = Find(root->left,q);
bool qInright = !qInleft;
if((pInleft&&qInright)||(qInleft&&pInright))
{
return root;
}
else
{
if(pInleft&&qInleft)
{
return _lowestCommonAncestor(root->left,p,q);
}
else{
return _lowestCommonAncestor(root->right,p,q);
}
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
//用子函数去找
TreeNode* ret = _lowestCommonAncestor(root,p,q);
return ret;
}
};
这个思路的时间复杂度会有点高,我们看思路二。
思路二:
如果我们有p和q到根节点的路径,那么这个问题就可以转化为相交链表的问题,但是这个树不是三叉链,我们怎么找路径呢,我们可以利用一个栈,把经过的节点都记录下来,然后找p或者q,然后去左边找如果找到就返回true,如果找不到就去右边找,找到就返回true,如果左右两边都没有找到,就说明这个子树不包含p或者q,我们就把栈里的元素pop一下并且返回false,直到找到为止,找到路径后就是链表相交的问题,我们让长的路径先走,然后路径一样长了,以后在一起走,直到相遇,就是公共祖先。
解题代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool Find(TreeNode* root, TreeNode* x, stack<TreeNode*>& s)
{
if(root==nullptr)
{
return false;
}
s.push(root);
if(root==x)
{
return true;
}
if(Find(root->left,x,s))
return true;
if(Find(root->right,x,s))
return true;
s.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
stack<TreeNode*> st1,st2;
Find(root,p,st1);
Find(root,q,st2);
while(st1.size()!=st2.size())
{
if(st1.size()>st2.size())
{
st1.pop();
}else
{
st2.pop();
}
}
while(st1.top()!=st2.top())
{
st1.pop();
st2.pop();
}
return st1.top();
}
};
从前序与中序遍历序列构造二叉树
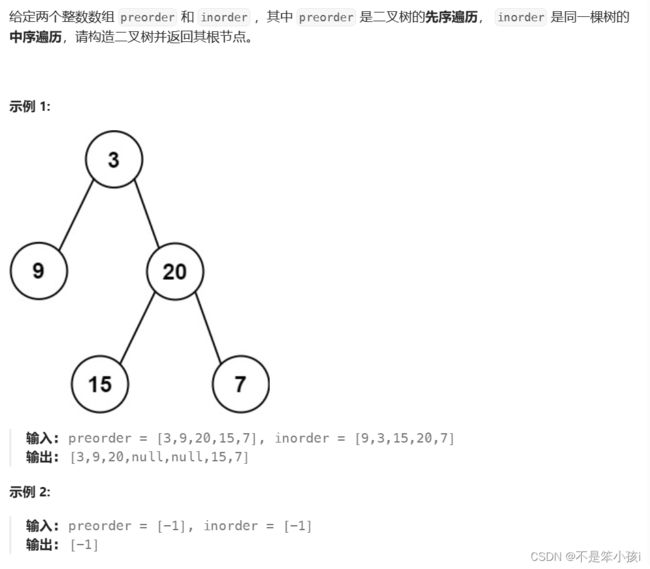
前序遍历是先根在左右子树,所以前序遍历的第一个值一定是根,而中序遍历是左子树 根 右子树,所以我们可以跟根在中序中分出来左右子树,然后构造根,在分别递归构造左右子树,但是我们需要直到当前遍历到那个位置,所以我们需要一个变量来记录,并且需要一段区间来记录左右子树在中序区间的范围。
解题代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int& i, int begin, int end)
{
if(begin>end)
{
return nullptr;
}
//构造根
TreeNode* root = new TreeNode(preorder[i]);
int curi = begin;
//找中序根的位置
while(preorder[i]!=inorder[curi])
{
curi++;
}
i++;
//构造左右子树
root->left = _buildTree(preorder,inorder,i,begin,curi-1);
root->right = _buildTree(preorder,inorder,i,curi+1,end);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
int i = 0;
TreeNode* ret = _buildTree(preorder,inorder,i,0,inorder.size()-1);
return ret;
}
};
二叉搜索树与双向链表
我们可以走一个中序遍历,先找到最左节点,然后在用一个前驱指针prev,保存上一个节点,然后在遍历到第二个节点的时候改变链接关系,把当前的左指向前驱指针,把前驱的右指向当前节点,直到中序走完,链表就有了。只不过我们还要找到头结点,我们从根一直找到最左节点就是根节点。
解题代码
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
void Inorder(TreeNode* root, TreeNode*& prev)
{
if(root==nullptr)
{
return;
}
Inorder(root->left,prev);
root->left = prev;
//防止对空指针的解引用
if(prev)
{
prev->right = root;
}
prev = root;
Inorder(root->right,prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
TreeNode* prev = nullptr;
Inorder(pRootOfTree,prev);
while(pRootOfTree&&pRootOfTree->left)
{
pRootOfTree = pRootOfTree->left;
}
return pRootOfTree;
}
};
那么今天的分享就到这里了,有什么不懂得可以私信博主,或者添加博主的微信,欢迎交流。