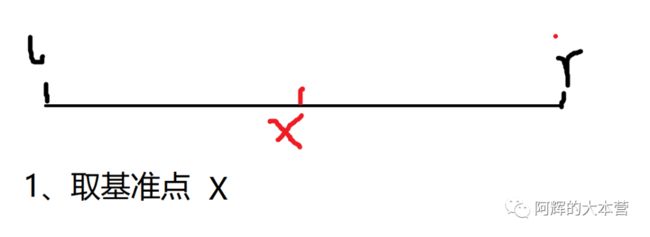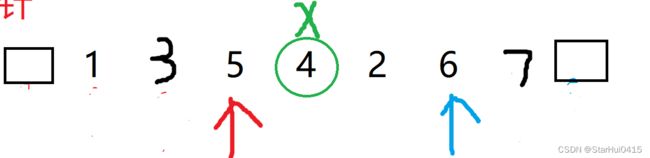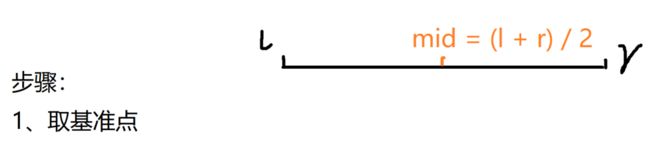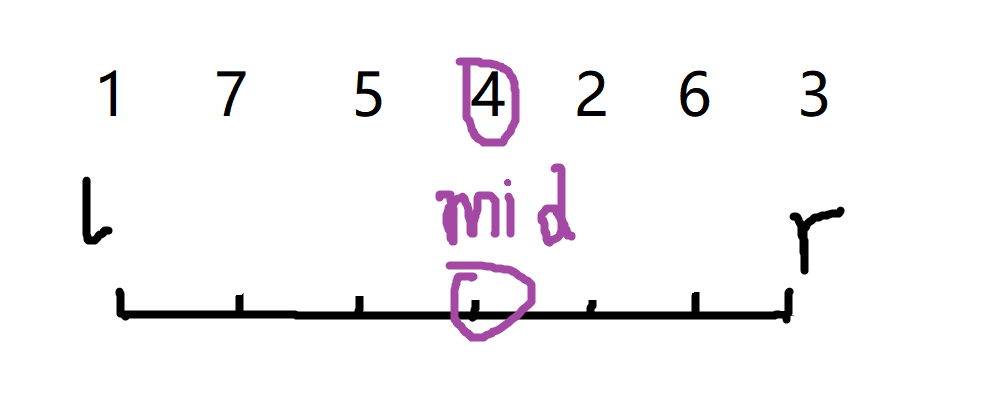AcWing算法基础课 第一讲小结(已完结,第二讲已开始)
目录
目录
前言
一、快速排序法及其扩展
快速排序法
介绍
思路 + 步骤
模拟代入
模板
练习
扩展(求第k个数)
思路
代码
二、归并排序法
归并排序
思路
思路 + 步骤
模拟代入
模板
练习
应用(逆序对的数量)
介绍
思路
模拟代入
模板
练习
三、二分
整数二分
大致步骤
详细步骤(两模板)
模板
模拟代入
练习
实数二分
介绍
练习
四、高精度算法
介绍
高精度加法
不压位步骤
压位步骤
练习
高精度减法
介绍
练习
高精度乘法
高精度乘以低精度
高精度乘以高精度
高精度除法
高精度除以低精度
高精度除以高精度
五、前缀和与差分
前缀和
介绍+思路
模板
练习
扩展
思路
练习
差分
介绍 + 思路
步骤
练习
扩展
思路
模板
举例
练习
六、双指针算法
介绍
示例
应用1(最长连续不重复子序列)
编辑思路
模拟
代码
应用2(数组元素的目标和)
思路
代码
应用3(判断子序列)
思路
模拟
代码
七、位运算
八、离散化
九、区间合并
前言
在学习完C语言后,并刷了许多道题发现刷题暂时不适合我了,应该去学习新的知识点于是开始学习y总的算法基础课。经过了一个月,差不多已经弄懂了第一讲的内容,特来向大家分享,可能有错误之处,希望大家见谅!
之前在公众号上发过这样的文章,但是公众号没有目录,也没人看,就专门来CSDN上发。感兴趣的可以关注我的公众号:阿辉的大本营。每天会分享一道算法题,感兴趣的可以关注一下公众号!!!
一、快速排序法及其扩展
快速排序法
介绍
快速排序法的核心思想是分治。
分治就是把一个大问题分为两个或以上的相同子问题,再把子问题分为更小的子问题...直到子问题可以直接简单求解为止,这是原问题的解就是子问题解之和。
快速排序是通过使用分治法策略把一个串行分为两个子串行。快速排序又是分而治之在排序算法上的典型应用。
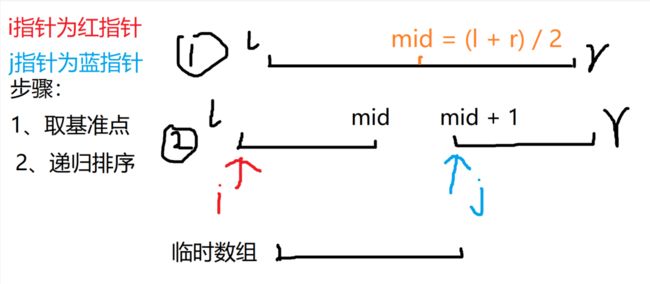
思路 + 步骤
1、取基准点
在这个数组里面取一个点作为基点,可以取左端点、右端点、中间值、随机取
2、划分区间
遍历整个数组,把小于基准点的放在左边,大于基准点的放在右边。传统方法是:开两个数组,分别把元素存里面。这里使用双指针算法,定义两个指针,分别从两边往中间走,当满足条件时就继续走,一个不满足条件时就停止原地,等待另一个指针不满足条件,之后两个指针指向的元素互换;再接着往下走,直至走到基准点!!!
3、递归排序左右两边
这一步也是和上面一样,把小于基准点的区间和大于基准点的区间再次重复1、2操作。当递归结束,数组就已经排好序了。需要注意的是,递归函数的退出。递归排序区间时,到最后区间元素个数就为1,那这时候怎样退出递归呢?需要在quick_sort()函数里面写个判断条件,当区间元素个数为1时,就退出。
模拟代入
现在上一个实例,来给大家模拟一下快速排序法的过程,帮助大家理解!!!
如果题目给了我们一个数组,让我们对这个数组进行排序。这个数组为{1, 7, 5, 4, 2, 6, 3}。
1、取基准点
可以随便取,也可以去左右端点,也可以取中间值
2、划分区间
区间是通过双指针算法来划分的,让一个指针从数组最前面的元素的前一位 和 另一个指针从数组的最后一位元素的下一位 同时往中间走。然后判断是否满足条件
开始
两个指针先往中间走一位
此时,i指向的元素小于基准点,j指向的元素小于基准点。然后 j指针跳出do while循环(不满足do while循环条件)j = 6。但是i指针还是支持往后走 。还没有轮到后面的if(i < j)语句执行
此时 i 指针指向的元素大于基准点,不满足do while循环条件,跳出do while循环,i = 2;现在两个指针都跳出了 do while循环,可以执行if语句了,正好条件为真,于是这两个指针指向的元素互换
然后 i 指针和 j 指针继续进入do while循环
此时 i 指针指向的元素大于基准点,i 跳出do while循环,i = 2;但是 j 指针指向的元素大于基准点,继续往中间走。不执行if语句
此时 j 指针指向的元素小于基准点,跳出do while循环,j = 4;执行if语句,正好满足条件,就两个指向的元素进行互换
互换后,两个指针1继续往中间走,走到了基准点,while循环结束,代表区间划分已经结束了,左边的区间都小于基准点,右边的区间都大于基准点
3、递归排序左右区间
就是重复以上的1、2步操作,就是区间变小了而已
最后再来一个动图,再帮大家理解一下(动图来自菜鸟教程)
模板
void quick_sort(int nums[],int l,int r)
{
if(l >= r)//判断是否只有一个元素或者没有元素
return;//如果没有直接退出函数
int i = l - 1,j = r + 1,x = nums[(l + r) / 2];
//i取左端点的的前面一位,j去右端点的右边一位;方便使用do while循环
//先往前走一位再判断,如果不这样,会把第一位和最后一位漏掉。基准点随便取
while(i < j)
{
do i++;while(nums[i] < x);//当满足小于基准点时,继续往下走
do j--;while(nums[j] > x)//与i一样
if(i < j)//当i和j跳出do while循环,说明都不满足条件,需要互换
{
swap(nums[i],nums[j]);
//这个是头文件为algorithm的标准库函数,如果没有的话这样写
//int t = nums[i];
//nums[i] = nums[j];
//nums[j] = t;
}
}
//经过上面循环操作,已经划分好区间了,下面就是递归排序左右区间了
quick_sort(nums,l,j);//递归排序左区间
quick_sort(nums,j + 1,r);//递归排序右区间
//当基准点为数组中间元素,必须这样写,不然排序错误
}练习
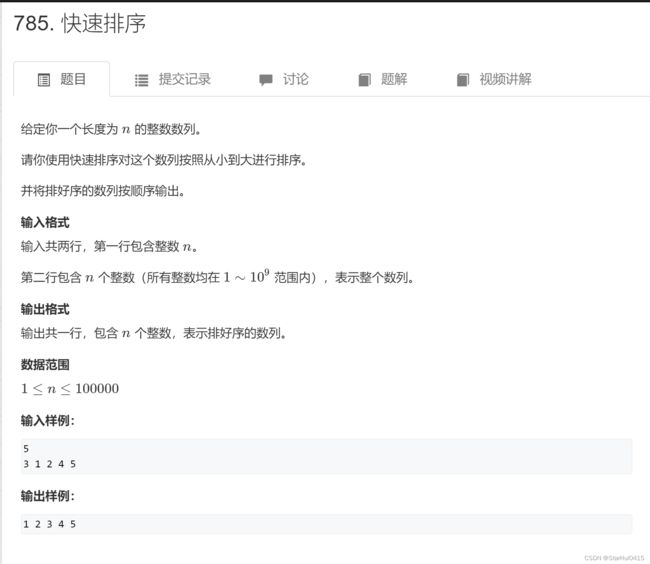
学习了以上内容后,快来试一下模板好用不好用吧!练习一道小题
看完题了吧,很简单的。下面是题解
#include
#include
using namespace std;
const int N = 1e5 + 10;
int nums[N];
void quick_sort(int nums[],int l,int r)
{
if(l >= r)
return;
int i = l - 1,j = r + 1,x = nums[(l + r) / 2];
while(i < j)
{
do i++;while(nums[i] < x);
do j--;while(nums[j] > x);
if(i < j)
swap(nums[i],nums[j]);
}
quick_sort(nums,l,j);
quick_sort(nums,j + 1,r);
}
int main()
{
int n;
cin >> n;
for(int i = 0;i < n;i++)
cin >> nums[i];
quick_sort(nums,0,n - 1);
for(int i = 0;i < n;i++)
cout << nums[i] << ' ';
return 0;
} 扩展(求第k个数)
学习完快速排序法后,我们应该知道快速排序法并不是只能超快排序的,还能进行一些操作,比如快速找到从小到大的第k个数。趁热打铁,赶紧来讲一下怎么可以快速选出第k小的数。
思路
让我们来回忆一下快速排序法的步骤。第一步:取基准点。第二步:划分区间。第三步:递归排序左右两边。找到第k小的数,只需要改变第三步。为什么呢?题目没有让我们排序,只是让我们找到第k小的数,只需要比较一下左区间的元素个数(sl) 与 k的大小,如果sl大于k,就说明答案在左区间,递归排序左边;反之答案在右区间,就递归排序右边。注意:此时区间元素个数为1时,要返回这个元素。
代码
#include
#include
using namespace std;
const int N = 1e5 + 10;
int nums[N];
int quick_sort(int nums[],int l,int r,int k)
{
if(l >= r)
return nums[l];//返回nums[r]也是这个结果,因为递归结束时,i = j
int i = l - 1,j = r + 1,x = nums[(l + r) / 2];
while(i < j)
{
do i++;while(nums[i] < x);
do j--;while(nums[j] > x);
if(i < j)
swap(nums[i],nums[j]);
}
int sl = j - l + 1;//统计左区间元素个数
if(sl >= k)//如果sl大于等于k,说明答案在左边
return quick_sort(nums,l,j,k);
else//反之在右边
return quick_sort(nums,j + 1,r,k - sl);
}
int main()
{
int n,k;
cin >> n >> k;
for(int i = 0;i < n;i++)
cin >> nums[i];
cout << quick_sort(nums,0,n - 1,k) << endl;
return 0;
} 二、归并排序法
归并排序
思路
归并排序是建立在归并操作上的有效的排序算法,该算法的核心是分治。这个分治与快速排序法的分治不同,快速排序法是用数组元素分治,归并排序是用下标分治
思路 + 步骤
1、取基准点(是数组下标而不是数组元素)
2、递归排序左右区间
关于这个递归排序左右区间,递归后就排好序了,大家可能不能理解为什么可以排好序,等第三步写出来就知道了,
3、归并-合二为一
怎么合二为一呢?此时我们需要一个额外的临时数组来暂时存储排完序的数组。然后利用双指针算法,从这两个区间的首元素开始走,来比较左右区间里面的元素,
谁最小,谁先存储到临时数组。
但是当这一步结束时,可能会存在一个区间指针已经把元素走完了,但是另一个区间还有元素没有走完;
所以需要在这一步后面再加上两个while循环,把没有走完的元素存储到临时数组里面,防止特殊情况发生。
看完第三步,应该理解了第二步是怎么利用递归排序的吧!
模拟代入
假如题目给我们一个数组,让我们进行排序。这个数组为{1, 7, 5, 4, 2, 6, 3}。
1、取基准点
基准点推荐去数组的中间元素的下标
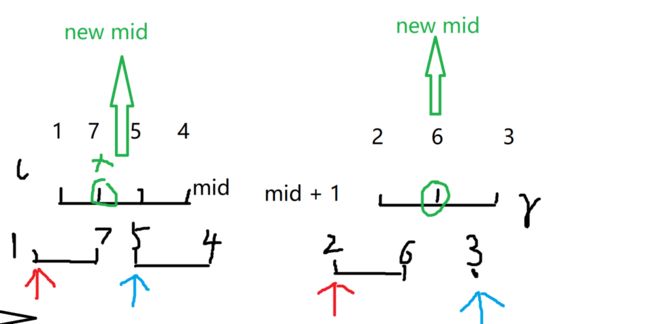
2、递归排序左右区间
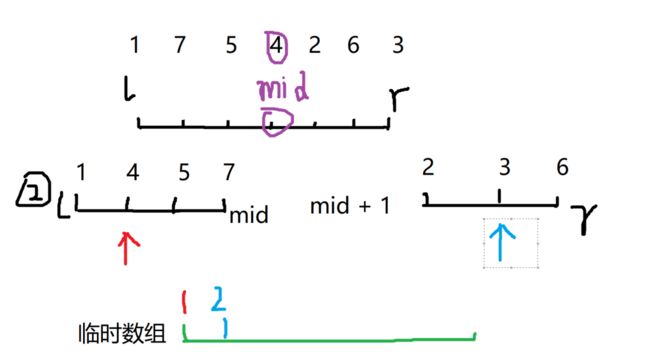
以基准点为分界点,把[l,mid] 和 [mid + 1,r]递归排序。现在来看一下
取新基准点
双指针算法,存临时数组
最后两个while循环把没有存到临时数组里面的元素存进去
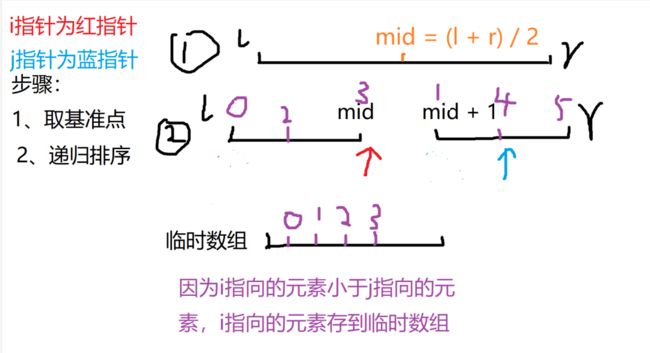
3、合并--合二为一
当左右区间排完序后,就开始利用双指针算法,从这两个区间的首元素开始走
将指针指向的元素和j指针指向的元素进行比较,如果谁最小,谁就被存到临时数组里面。
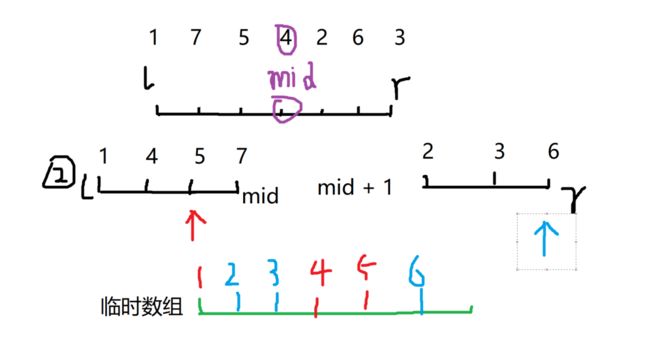
直到一个指针走到末尾结束。
此时一个区间已经遍历完了,但是另一个区间还有一个元素。这该怎么办呢?这就是下面的两个循环的作用了,让那些没用遍历完的区间的元素继续遍历,直到到末尾,并把剩下的元素存到临时数组。
再给大家放一下归并排序的动图,帮助大家更快地逻辑(来自菜鸟教程)
模板
void merge_sort(int nums[], int l, int r)
{
if (l >= r) return;//如果数组只有1个元素,就退出,递归的结束条件
int mid = l + r >> 1;//取基准点
merge_sort(nums, l, mid), merge_sort(nums, mid + 1, r);//递归排序左右区间
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)//利用双指针算法,来排序
{
if (nums[i] <= nums[j]) //谁最小谁先存到临时数组里面
tmp[k ++ ] = nums[i ++ ];
else
tmp[k ++ ] = nums[j ++ ];
}
while (i <= mid) //防止左区间没有遍历完
tmp[k ++ ] = nums[i ++ ];
while (j <= r) //防止右区间没有遍历完
tmp[k ++ ] = nums[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) //物归原主,把排好序的临时数组赋值给原数组
nums[i] = tmp[j];
}练习
#include
using namespace std;
const int N = 1e5 + 10;
int nums[N],tmp[N];
void merge_sort(int nums[],int l,int r)
{
if(l >= r)//如果数组只有一个元素,就退出,既用在刚开始判断是否只有1个元素,也作为递归的结束条件
return;
int mid = (l + r) / 2;
merge_sort(nums,l,mid),merge_sort(nums,mid + 1,r);//递归排序左右区间
int i = l,j = mid + 1,cnt = 0;
while(i <= mid && j <= r)//双指针,比较指针指向的元素大小
{
if(nums[i] <= nums[j])//谁小,谁先存到临时数组
tmp[cnt++] = nums[i++];
else
tmp[cnt++] = nums[j++];
}
while(i <= mid)//这两个while循环,是为了防止指针没有走完,还有元素没有存到临时数组
tmp[cnt++] = nums[i++];
while(j <= r)
tmp[cnt++] = nums[j++];
for(i = l,j = 0;i <= r;i++,j++)//物归原主,把排好序的数值赋值给原数组
nums[i] = tmp[j];
}
int main()
{
int n;
cin >> n;
for(int i = 0;i < n;i++)
cin >> nums[i];
merge_sort(nums,0,n - 1);
for(int i = 0;i < n;i++)
cout << nums[i] << ' ';
cout << endl;
return 0;
} 应用(逆序对的数量)
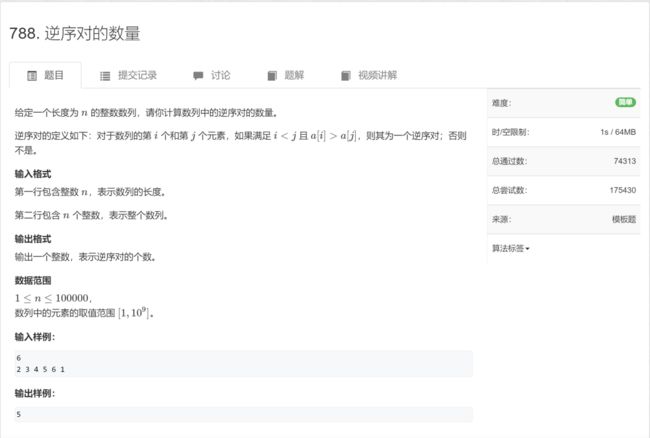
介绍
在做这道题之前,我们先来了解一下逆序对,看一下百度百科上的解释
估计看着比较懵,举个例子,数组为{3,2,1,5,4},3和2、1都是逆序对;逆序对是从数组里面选两个数,前面的数字比后面大。
逆序对的数量求解有三种做法,分别是 枚举法(双层for循环)、归并排序法、树状数组;目前我只会前两种,本题解是用归并排序来做。还是分治的思想。为什么可以用归并排序来做呢?不知道你们有没有思考过。
思路
归并排序是把一个区间一分为二,递归排序左右区间,然后使用两个指针比较大小,谁指向的元素小,那个小的元素就先存到数组里面。比较大小,逆序对不就是前面的数字比后面的数字大吗?此时,完全可以通过比较大小,来记录逆序对的数量!!!那么在归并排序里面,逆序对不是只有一种情况,一共有三种情况。分别为:左区间的逆序对、右区间的逆序对、一个在左区间一个在右区间的逆序对,如图所示(鼠标画的难受,凑合看看吧)
此时这三种情况的逆序对数量怎么求呢?
第一种情况:左区间逆序对的数量等于 merge_sort(nums,l,mid)
第二种情况:右区间逆序对的数量等于 merge_sort(nums,mid + 1,r)
为什么这两种情况可以求出左右区间的数量?请特别注意递归,看第三种情况。
第三种情况:此时左右区间都已经排好序了,如果不理解的话,往上翻一下,再看看归并排序。
当两个指针指向的元素进行比较时,如果第一个指针的元素大于第二个,说明i指针后面的元素(包含i指针)都比此时j指针指向的数大,都构成了逆序对,因为左右区间是升序!!!,此时逆序对数量为mid - i + 1。为什么加1?因为这是数组下标,是从0开始的,要加1。
注意:此时i指针前面的元素都小于j指针此时指向的元素,因为当 i 指针动时,说明左区间的元素比右区间的小,且区间都是升序的。
模拟代入
假如题目给我们一个数组,让我们求逆序对的数量。这个数组为{1, 7, 5, 4, 2, 6, 3}。
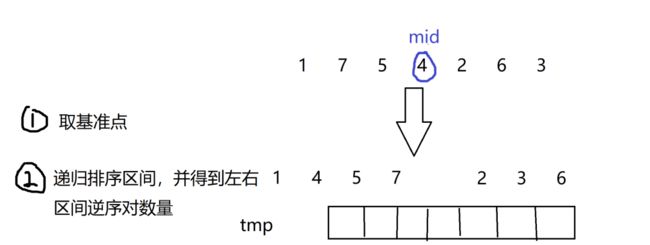
1、取基准点
2、递归排序左右区间并且得到左右区间的逆序对数量
现在不明白没关系,看第三步
3、求一左一右元素的逆序对
使用两个指针遍历左右数组
当i指针指向的元素小于j指针指向的元素时,把i指针的元素存到临时数组,继续往下走
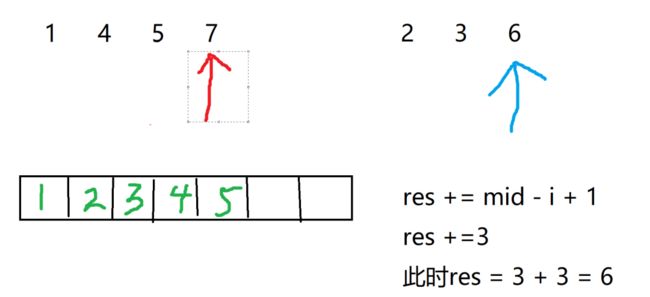
当i指针指向的元素大于j指针指向的元素时,逆序对数量为midmid - i + 1,因为区间是升序,i指针以及后面的元素都大于j指针指向的元素,都是逆序对
j指针往后走,再次比较大小
j指针的元素还是小于i指针的元素,还是res += mid - i + 1;把小的元素存进去,j指针后移
后移后
再比较指针指向的元素大小,i指针小于j指针指向的元素,小元素存入数组,逆序对数量不变。
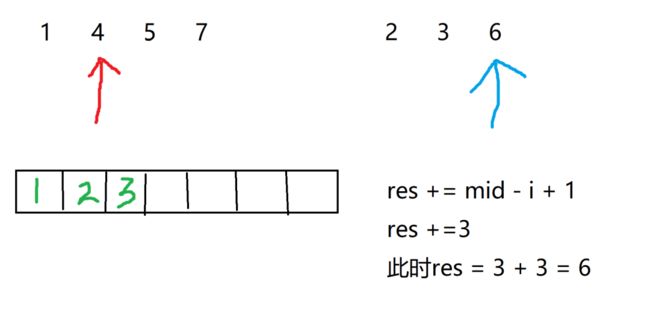
i指针指向的元素还是小于j指针,i指针指向的元素存入临时数组,逆序对不变
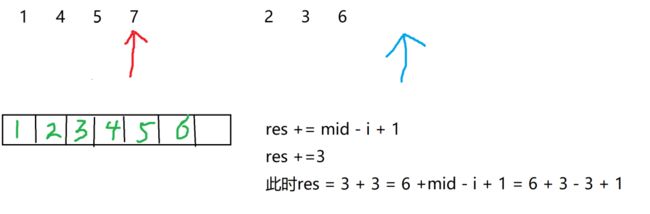
此时i指针指向的元素大于j指针指向的元素,逆序对再加上mid - i + 1;
这是左右区间逆序对的数量。看完第三步后,第二步应该知道是为什么可以得到左右区间的逆序对的数量了吧,就是区间变成各自区间的一半后进行重复操作而已!!!
模板
long long merge_sort(int nums[],int l,int r)
{
if(l >= r)
return 0;//数组只有一个元素,退出函数,也做函数递归的结束条件
int mid = (l + r) / 2;//取基准点
//得到左区间里面和右区间里面的逆序对的数量
long long res = merge_sort(nums,l,mid) + merge_sort(nums,mid + 1,r);
int i = l,j = mid + 1,cnt = 0;//两个指针,和临时数组下标
while(i <= mid && j <= r)
{
//如果i指针指向的元素小于j指针的,把i指针的元素存入数组
if(nums[i] <= nums[j])
tmp[cnt++] = nums[i++];
//i指针元素大于j指针的,说明此时i指针以及之后的元素都比现在j指针的大
//是逆序对,
else
{
res += mid - i + 1;
tmp[cnt++] = nums[j++];
}
}
while(i <= mid)//防止指针没有走完左区间
tmp[cnt++] = nums[i++];
while(j <= r)//防止指针没有走完右区间
tmp[cnt++] = nums[j++];
for(int i = l,j = 0;i <= r;i++,j++)//物归原主
nums[i] = tmp[j];
return res;
}练习
先不要向下看,等下再来看代码
#include
using namespace std;
typedef long long LL;//给long long起个别名,太长了
const int N = 1e5 + 10;
int nums[N],tmp[N];
LL merge_sort(int nums[],int l,int r)
{
if(l >= r)
return 0;
int mid = (l + r) / 2;
LL res = merge_sort(nums,l,mid) + merge_sort(nums,mid + 1,r);
int i = l,j = mid + 1,cnt = 0;
while(i <= mid && j <= r)
{
if(nums[i] <= nums[j])
tmp[cnt++] = nums[i++];
else
{
res += mid - i + 1;
tmp[cnt++] = nums[j++];
}
}
while(i <= mid)
tmp[cnt++] = nums[i++];
while(j <= r)
tmp[cnt++] = nums[j++];
for(int i = l,j = 0;i <= r;i++,j++)
nums[i] = tmp[j];
return res;
}
int main()
{
int n;
cin >> n;
for(int i = 0; i < n;i++)
cin >> nums[i];
cout << merge_sort(nums,0,n - 1) << endl;
} 三、二分
二分,就是一分为二。就是在有序序列里面,通过不断地二分,进而缩小解的范围,从而更快地寻找满足条件的解。
本质:如果可以找到某种性质,使得整个区间一分为二,其中一半区间满足条件,另一半区间不满足条件;二分就可以寻找性质的边界。
整数二分
整数二分稍微有点复杂,主要是需要处理边界问题,比较麻烦,不过还是挺简单的。整数二分主要有两种情况,第一种情况是把区间分为[l,mid] 和[mid + 1,r];第二种是把区间分为[l,mid - 1] 和[mid,r];现在大家可能不知道这是什么意思,没关系看下去。下面我会介绍什么时候怎么划分区间!
大致步骤
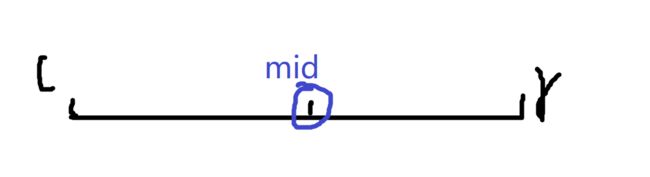
1、取中间值mid
注意这个中间值和前面的归并排序一样,取的是数组元素的下标,并不是数组元素。
而mid = (l + r) / 2或者mid = ( l + r + 1) / 2;看情况取
2、判断mid是否满足某种性质
什么意思呢?就是判断此时的基准点的右边满足某种性质,基准点的左边都不满足这种性质,就可以把整个区间一分为二,一半满足一半不满足。那么二分就可以寻找这两个性质的边界。
而寻找这两种不同的边界,就是两个不同的模板。让我们来看看这两个不同的模板吧。
详细步骤(两模板)
a、寻找红颜色性质的边界
先取中间值mid = (l + r) / 2(先不加一),然后每次判断一下中间值是否满足红颜色的性质。此时有两种情况。
第一种是满足,即true,说明mid在红色区间里面
既然知道了在红颜色里面,而我们要寻找红颜色的边界,所以答案在mid右边,包含mid;此时把一个区间一分为二,分成[l,mid - 1] 和 [mid + 1,r];更新方式为l = mid;
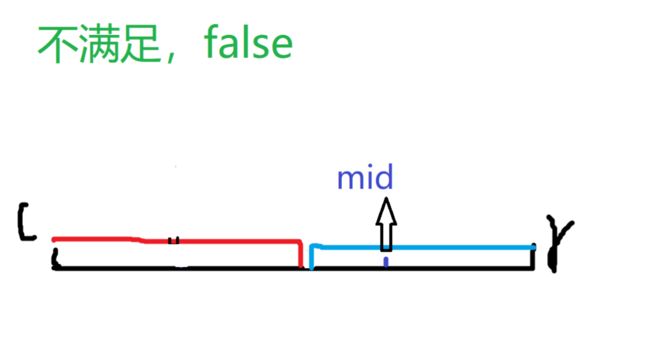
第二种是不满足,即false,说明mid在蓝色区间里面。
既然mid在蓝色区间里面,而我们要寻找红颜色的边界,所以答案一定在mid - 1的左边(包含mid - 1)为什么一定不包含mid呢?因为mid在蓝颜色区间里面,一定不能满足红颜色区间的性质。至多mid的前一位mid - 1满足。更新方式是r = mid - 1;看到这里,我们前面mid取值要加上1,mid = (l + r + 1)/ 2。
为什么要加1?因为C++里面除法是向下取整,当l = r - 1时,mid = (l + r)/2。此时mid = l(向下取整),而如果check()成功了,更新方式为l = mid;这不是一个死循环吗?所以为了防止死循环,所以要加1,变成向上取整,mid = r。
b、寻找蓝颜色的边界点
先取中间值mid,mid = (l + r )/ 2;然后每次判断是否满足蓝颜色的性质,此时判断有两种情况
第一种是满足,即true,说明mid在蓝颜色区间里面
既然已经知道mid在蓝颜色区间里面,而我们要寻找蓝颜色的边界,所以答案一定在mid左边(包含mid,因为mid1在蓝颜色区间里面)。所以整个区间就被一分为二成两个区间,[l,mid],[mid + 1,r]。更新方式为r = mid;
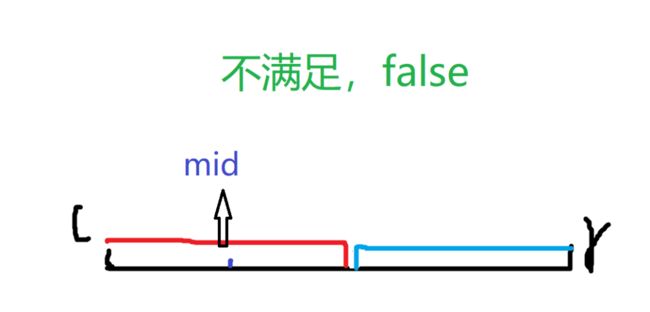
第二种是不满足,即false,说明mid在红色区间里面
既然知道了mid在红色区间里面,我们要寻找蓝颜色边界,所以答案一定在mid右边(不包含mid,因为mid在红颜色区间里面),更新方式为l = mid + 1;
模板
区间被划分为[l,mid - 1] 和 [mid,r];
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;//取中间值
if (check(mid)) //判断是否满足某种性质
l = mid;//更新区间
else
r = mid - 1;
}
return l;
}区间被划分为[l,mid] 和 [mid + 1,r]
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;//取中间值
if (check(mid)) //判断满足某种性质
r = mid;//更新区间
else
l = mid + 1;
}
return l;
}模拟代入
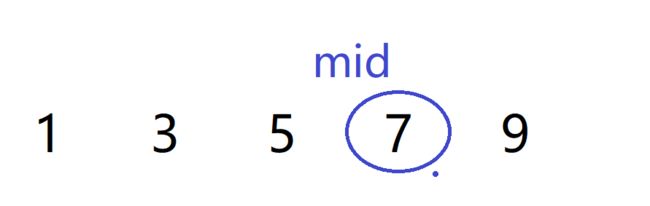
如果给你一个数组nums,为{1,3,5,7,9}。让你查找第一个大于等于6的数字的下标
1、取中间值mid
不管三七二十一,先把mid = (l + r) / 2;等到后面再看区间是怎么划分的,然后再决定加不加1;
2、判断mid是否满足某种性质
这个题是寻找蓝色区间边界,也就是第二个模板。
mid的下标为2,nums[mid] = 5,小于题目要找的元素,所以答案在右边,更新区间,l = mid + 1,更新后的mid = (3 + 4)/ 2,向下取整为3
此时mid大于6,且左边的都小于5,右边的都大于6,所以返回这个数的下标。
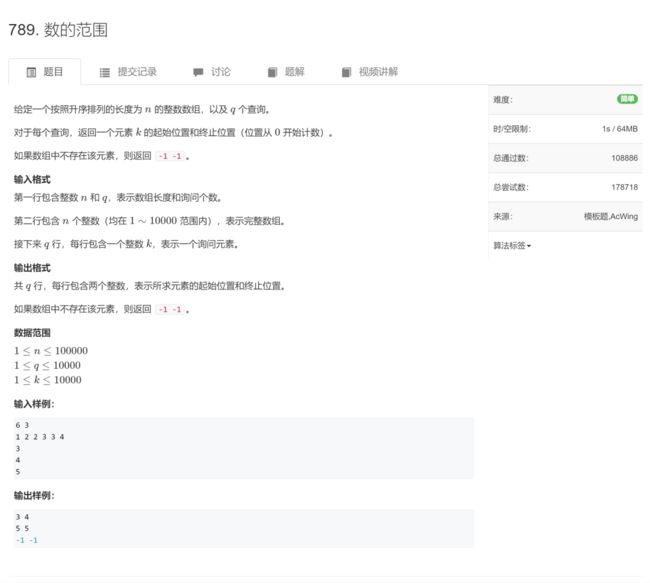
练习
大家先不要着急看代码啊,自己静下心来,认真思考一下!!!
代码
#include
using namespace std;
const int N = 1e6 + 10;
int nums[N];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i = 0;i < n;i++)
scanf("%d",&nums[i]);
while(m--)
{
int x;
scanf("%d",&x);
int l = 0,r = n - 1;
//求元素起始位置
while(l < r)
{
int mid = (l + r) / 2;
if(nums[mid] >= x)//由于mid也满足,答案在[l,mid]
r = mid;//更新区间
else
l = mid + 1;
}
if(nums[l] != x)//判断nums[l]和判断nums[r] 结果是一样的,因为当while循环结束,l = r
cout << "-1 -1" << endl;
else//求元素终止位置
{
cout << l << ' ';//或者cout << r << ' ';因为l和r相等
int l = 0,r = n - 1;
while(l < r)
{
int mid = (l + r + 1) / 2;//为了防止死循环,+1
if(nums[mid] <= x)//由于mid也满足,所以答案在[mid,r];
l = mid;//更新区间
else
r = mid - 1;
}
cout << r << endl;
}
}
return 0;
} 实数二分
介绍
实数的二分比较简单,由于比较稠密,可以被整除,所以没有什么边界问题,不需要加1。核心是精度的确定,一般有两种方法。第一种是r -l>esp;esp = 10^-(k + 2),k为要保留的位数;第二种方法是不管三七二十一,for循环100次差不多就可以得到精确的数了。
double b_sreach(double l,double r)
{
while(r - l > esp)//确定精度
{
double mid = (l + r) / 2;
if(check())
r = mid;
else
l = mid//不同于整数,不需要加1
}
return l;//return r;
}或
double b_search(double l,double r)
{
for(int i = 0;i < 100;i++)//直接循环100次
{
int mid = (l + r) / 2;
if(check())
r = mid;
else
l = mid;
}
return l;//return r
}实数二分很简单的,重要的是精度的确定。现在大家都理解了吧,下面让我们来一起练习一下吧!
练习
不要着急看哦,自己思考一下,看看能不能做出来,再继续往下看
#include
using namespace std;
int main()
{
double x;
cin >> x;
double l = -100,r = 100;
while(r - l > 1e-8)
{
double mid = (l + r) / 2;
if(mid * mid * mid >= x)
r = mid;
else
l = mid;
}
printf("%.6lf",l);
return 0;
} 四、高精度算法
介绍
高精度算法是处理大数字的数学计算方法,在一般的科学的计算中,会经常算到小数点后几百位或者更多,当然也可能是几千亿几百亿的大数字。一般这类数字我们统称为高精度数。
高精度算法是用计算机对于超大数据的一种模拟加,减,乘,除,乘方,阶乘,开方等运算。对于非常庞大的数字无法在计算机中正常存储,于是,将这个数字拆开,拆成一位一位的,或者是四位四位的存储到一个数组中, 用一个数组去表示一个数字,这样这个数字就被称为是高精度数。高精度算法就是能处理高精度数各种运算的算法。
下面将会讲解四种常见的高精度计算,包括高精度加法、减法、高精度乘低精度、高精度除低精度;再加一个高精度乘高精度。其中还包括压位操作。
这几种操作会有重复操作,本篇文章只会在高精度加法里面详细讲解一下,后面的就简单说一下。
高精度加法
不压位步骤
第一步:数据的存储
首先,我们需要考虑的是,当我们用字符串接收数据后,用什么存储数据呢?常见的有两种,第一种就是数组,第二种是vector容器。由于vector容器自带size函数,所以本文采用vector容器存储数据。
第二,我们是正序存储数据,还是倒序存储数据呢?这里推荐使用倒序。为什么呢?因为加法可能存在进位,举个例子,由四位数进位到五位数,如果是正序存储的话,就需要把元素都后移一位,比较麻烦。而如果是倒序的话,就直接在末尾添加元素就可以了,十分方便。
for(int i = a.size();i >= 0;i--)
A.push_back(a[i] - '0');
for(int i = b.size();i >= 0;i--)
B.push_back(b[i] - '0');第二步:人工模拟加法
数据处理完了,就开始进行加法操作。这个是核心,人工模拟加法,就是用代码模拟出小时候学习加法的操作。
如果低位数相加大于10的话,就减去10,得到余数;如果小于10的话,就不变。在用计算机语言进行该操作时,无论相加的结果是大于10还是小于10,直接进行取余(%)操作,就能得到准确的结果。
还有一个需要注意的是,当两个数的对应位数相加之前,要判断当前位数是否存在数字,然后决定是否相加。
vector add(vector &A,vector &B)
{
//判断两个数位数,以此保证第一个参数的位数大于第二个参数
if(A.size() < B.size())
return add(B,A);
vector C;//储存结果
int t = 0;//进位
for(int i = 0;i < A.size();i++)
{
t += A[i];//先加上A上的数
if(i < B.size())//如果B位数有数,那么也加上
t += B[i];
C.push_back(t % 10);//得到该位数的数字
t /= 10;//用于进位
}
if(t)//判断最后的t是否为0,如果不为零,说明还需要进位
C.push_back(t);
return C;//返回结果
} 压位步骤
首先我们先来了解一下压位。当数据过大时,此时long long存储不下,因此需要vector或者数组存储,然后计算。
而一般vector或者数组中的每一个元素是int,如果每一个位置只是存储0~9一位数字的话,比较浪费空间,并且计算也比较慢。因此可以让每个位置存储连续的多位数字,这被称为压位。
注意:加法可以压九位;乘法一般压四位,不能压五位,因为十万的平方爆int了
第一步:压位存入容器
既然是压位,就自然不能和不压位的那样一位一位的存到数组里面,而是要满九位或者是遍历完字符串了,才能存到容器里面。既然是倒序存入容器,就涉及到反转问题。
//s表示反转后数字,j为计数器,t用来反转数字
for(int i = a.size() - 1,s = 0,j = 0,t = 1;i >= 0;i--)
{
//得到数字反转的结果
s += (a[i] - '0') * t;
t *= 10,j++;
//当j等于9,或者字符串遍历完了,就把这几位数字存到容器了了里面
if(j == 9 || i == 0)
{
A.push_back(s);
s = j = 0;
t = 1;
}
}第二步:人工模拟加法
和上面不压位的大致一样,就是取余的底数变了,不是10,而是1000000000,因为想要得到九位数上的个数,必须要%1000000000。说不清楚,自己脑补一下吧。
//base在函数外面已经定义过了,为1e9
vector add(vector &A,vector &B)
{
if(A.size() < B.size())
return add(B,A);
vector C;
int t = 0;
for(int i = 0;i < A.size();i++)
{
t += A[i];
if(i < B.size())
t += B[i];
//底数变了,想要得到九位数的余数,只能%1e9
C.push_back(t % base);
t /= base;
}
if(t)
C.push_back(t);
return C;
} 第三步:输出
输出也需要讲一下,因为是压九位操作的,所以输出时不满九位要补零。但是第一次输出比较特殊,不需要补零,其他的都需要补零。
cout << C.back();
for(int i = C.size() - 2;i >= 0;i--)
printf("%09d",C[i]);讲完了这些步骤后,让我们来练习一些吧!!!
练习
不要着急看题解哦,自己动脑思考一下,这样才知道自己前面懂了没有!
压位代码
#include
#include
using namespace std;
const int base = 1e9;
vector add(vector &A,vector &B)
{
if(A.size() < B.size())
return add(B,A);
vector C;
int t = 0;
for(int i = 0;i < A.size();i++)
{
t += A[i];
if(i < B.size())
t += B[i];
//底数变了,想要得到九位数的余数,只能%1e9
C.push_back(t % base);
t /= base;
}
if(t)
C.push_back(t);
return C;
}
int main()
{
string a,b;
cin >> a >> b;
vector A,B;
//s是结果数字;j是次数,等于9就把九位数字存到容器,t为反转操作的,用来控制位数
for(int i = a.size() - 1,s = 0,j = 0,t = 1;i >= 0;i--)
{
//得到数字反转的结果
s += (a[i] - '0') * t;
t *= 10,j++;
//当j等于9,或者字符串遍历完了,就把这几位数字存到容器了了里面
if(j == 9 || i == 0)
{
A.push_back(s);
s = j = 0;
t = 1;
}
}
//一样操作,处理b
for(int i = b.size() - 1,s = 0,j = 0,t = 1;i >= 0;i--)
{
s += (b[i] - '0') * t;
t *= 10,j++;
if(j == 9 || i == 0)
{
B.push_back(s);
s = j = 0;
t = 1;
}
}
auto C = add(A,B);
cout << C.back();//特殊处理第一位,不需要补0
//剩下的不行满九位数,不够的补0
for (int i = C.size() - 2; i >= 0; i -- ) printf("%09d", C[i]);
cout << endl;
return 0;
} 高精度减法
介绍
高精度减法和高精度加法差不了多少。存储数据方式一样。之后在进行减法之前,要判断减数和被减数大小,以此判断结果是正负。核心思想就是人工模拟减法。这个人工模拟减法主要在于借位,如果对应的位数不够减,就借高位数,因此高位数要减一。还有一步,注意可能有前导零(比如001),所以要进行删除前导零的操作,之后就是输出了。
下面就不讲解压位的步骤了,因为和加法差不多
第一步:数据的存储
在进行数据存储的方法和高精度加法一样,还是倒序,为什么呢?因为加减乘除要保持一致,这是因为,高精度不会单独出题,一出题就是加减乘除一起,方便格式统一,所以都用倒序。
for(int i = a.size() - 1;i >= 0;i--)
A.push_back(a[i] - '0');第二步:比较减数和被减数大小
在进行减法操作之前,必须对减数和被减数进行比较,以此判断结果正负,方便输出负号(-)。如果减数大于被减数,就不需要改动,直接传参即可;如果减数小于被减数,需要把这两个参数位置互换(减数变成被减数,被减数变为减数),然后输出负号,在输出参数位置互换的结果。这里比较大小时,自定义了一个函数
bool cmp(vector &A,vector &B)
{
if(A.szie() != B.size())//如果位数不同,直接返回bool值
return A.size() > B.size();
//位数相同只能比较对应位数的大小,由于从字符串存到容器里面是倒序
//所以容器的最后一位是该数字的最高位,从高位开始比较,返回bool值
for(int i = A.size() - 1;i >= 0;i--)
{
if(A[i] != B[i])
return A[i] > B[i];
}
//如果到这函数还没有返回值,就说明这两个数相等,返回true
return true;
} 第三步:人工模拟减法
还记得小学刚学减法的时候吗?先从低位开始减,如果此时减数上的数大于被减数上的数,就直接减;否则就往前借位加上10再减;而前一位在进行减法操作时需要减1,因为它被借位了。减法就是这个思想,大家应该可以轻松理解吧!
vector sub(vector &A,vector &B)
{
vector C;
for(int i = 0,t = 0;i < A.size();i++)
{
t = A[i] - t;//t表示借位,只能为0或1
if(i < B.size())
t -= B[i];
C.push_back((t + 10) % 10);//无论正负,加上10,求余数不影响
if(t < 0)//如果t小于0,说明需要借位
t = 1;
else//反之不需要借位
t = 0;
}
while(C.size() > 1 && C.back() == 0)//去重前导零
C.pop_back();
return C;
} 练习
先不要着急看代码,做一道题检测一下自己吧
不压位代码
#include
#include
using namespace std;
bool cmp(vector &A,vector &B)//比较函数
{
if(A.size() != B.size())//位数不同比位数
return A.size() > B.size();
for(int i = A.size() - 1;i >= 0;i--)//位数相同,比较对应位数的数的大小
{
if(A[i] != B[i])
return A[i] > B[i];
}
return true;
}
vector sub(vector &A,vector &B)
{
vector C;
for(int i = 0,t = 0;i < A.size();i++)
{
t = A[i] - t;//t表示借位,只能为0或1
if(i < B.size())
t -= B[i];
C.push_back((t + 10) % 10);//无论正负,加上10,求余数不影响
if(t < 0)//如果t小于0,说明需要借位
t = 1;
else//反之不需要借位
t = 0;
}
while(C.size() > 1 && C.back() == 0)//去重前导零
C.pop_back();
return C;
}
int main()
{
string a,b;
cin >> a >> b;
vector A,B;
for(int i = a.size() - 1;i >= 0;i--)//把数据存到容器里面
A.push_back(a[i] - '0');
for(int i = b.size() - 1;i >= 0;i--)
B.push_back(b[i] - '0');
vector C;
//比较减数和被减数大小,如果减数大于等于被减数,不变
if(cmp(A,B))
C = sub(A,B);
//反之,位置互换,同时输出负号
else
{
C = sub(B,A);
cout << '-';
}
for(int i = C.size() - 1;i >= 0;i--)
cout << C[i];
return 0;
} 压位代码
#include
#include
using namespace std;
const int N = 1e9;
bool cmp(vector &A,vector &B)//比较减数和被减数关系
{
if(A.size() != B.size())
return A.size() > B.size();
for(int i = A.size() - 1;i >= 0;i--)
{
if(A[i] != B[i])
return A[i] > B[i];
}
return true;
}
vector sub(vector &A,vector &B)
{
vector res;
for(int i = 0,t = 0;i < A.size();i++)
{
t = A[i] - t;
if(i < B.size())
t -= B[i];
res.push_back((t + N) % N);//这里要加上10都要变为1e9,因为压位为九位
if(t < 0)//t只能为0或1,因为要么不借位,要么借1
t = 1;
else
t = 0;
}
while(res.size() > 1 && res.back() == 0)//去除前导零
res.pop_back();
return res;
}
int main()
{
string a,b;
cin >> a >> b;
vector A,B;
for(int i = a.size() - 1,t = 1,j = 0,s = 0;i >= 0;i--)
{
s += (a[i] - '0') * t;//和昨天的的加法压位操作一样
t *= 10,j++;//s是反转后的数字,j用来计数
if(j == 9 || i == 0)//到九位或者遍历完了
{
A.push_back(s);
s = j = 0;
t = 1;
}
}
for(int i = b.size() - 1,t = 1,j = 0,s = 0;i >= 0;i--)
{
s += (b[i] - '0') * t;
t *= 10,j++;
if(j == 9 || i == 0)
{
B.push_back(s);
s = j = 0;
t = 1;
}
}
vector C;
if(cmp(A,B))//比较减数和被减数关系
C = sub(A,B);
else
{
C = sub(B,A);
cout << '-';
}
cout << C.back();//第一个最特殊,不满九位,不需要补零
for(int i = C.size() - 2;i >= 0;i--)//剩下的都需要补零
printf("%09d",C[i]);
cout << endl;
return 0;
} 高精度乘法
高精度乘法有两种,第一个是常见的高精度乘低精度;第二个是不常见的高精度乘以高精度。这两种思路有点不一样,分别讲一下思路。就不详细写步骤,比较都和什么的高精度加法减法差不多,就是核心代码不一样而已
高精度乘以低精度
核心思路
高精度乘以低精度的代码模拟操作,和咱们小时候学的乘法不一样。不论低精度是几位数,把低精度看成一个整体。
这样做的好处是不需要再把每一位相乘后的结果相加后再进位了,直接进位处理,比较简单方便。
下面咱们来看看,乘法操作的具体步骤,把低精度看成一个整体,乘以高精度的每一位数。
这样有点抽象,这样吧,来上一个实例
这个是不是有点小意外,不用在相加了,只需要看进位就可以了!!!
不压位模板
vector mul(vector &A,int b)
{
vector C;//存储结果
int t = 0;//进位
for(int i = 0;i < A.size();i++)
{
t += A[i] * b;//存储每一位数相乘的结果
C.push_back(t % 10);//得到该位的数字
t /= 10;//用来进位
}
if(t)//如果t != 0 说明还有进位,就把它添加到末尾
C.push_back(t);
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
} 这个模板有点麻烦,可以把后面的if语句和for循环合并起来,这样for循环的结束条件为i遍历完了,或者进位t处理完了!!!
vector mul(vector &A,int b)
{
vector C;//存储结果
int t = 0;//进位
//把if和for循环合并,结束循环有两种情况,i遍历完了或者t为空
for(int i = 0;i < A.size() || t;i++)
{
if(i < A.size())
t += A[i] * b;//低精度与高精度每一位数相乘的结果
C.push_back(t % 10);//该位数上的数字
t /= 10;//处理进位
}
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
}
压位模板
//C为结果,A*b,里面的N根据压几位而定,10^N
vector mul(vector &A,int b)
{
vector C;//存储结果
int t = 0;//进位
//把if和for循环合并,结束循环有两种情况,i遍历完了或者t为空
for(int i = 0;i < A.size() || t;i++)
{
if(i < A.size())
t += A[i] * b;//进位
C.push_back(t % N);//得到该位数的数字
t /= N;//处理进位
}
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
} 练习
不压位代码
#include
#include
using namespace std;
vector mul(vector &A,int b)
{
vector C;//存储结果
int t = 0;//进位
//把if和for循环合并,结束循环有两种情况,i遍历完了或者t为空
for(int i = 0;i < A.size() || t;i++)
{
if(i < A.size())
t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while(C.size() > 1 && C.back() == 0)
C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector A;
for(int i = a.size() - 1;i >= 0;i--)//存到容器A
A.push_back(a[i] - '0');
auto C = mul(A,b);
for(int i = C.size() - 1;i >= 0;i--)
cout << C[i];
cout << endl;
return 0;
} 压四位代码
因为int类型只能压四位,10000*10000就会爆int
#include
#include
using namespace std;
const int N = 10000;//超过4位会爆int
vector mul(vector &A,int b)
{
vector C;//存储结果
int t = 0;//进位
//把if和for循环合并,结束循环有两种情况,i遍历完了或者t为空
for(int i = 0;i < A.size() || t;i++)
{
if(i < A.size())
t += A[i] * b;
C.push_back(t % N);
t /= N;
}
while(C.size() > 1 && C.back() == 0)
C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector A;
//s为反转后的数,j为计数器,t为反转用的
for(int i = a.size() - 1,j = 0,s = 0,t = 1;i >= 0;i--)//存到容器A
{
s += (a[i] - '0') * t;
t *= 10,j++;
if(j == 4 || i == 0)//压4位
{
A.push_back(s);//当输入容器里面后,必须把那些重复使用的元素,重新初始化
s = j = 0;
t = 1;
}
}
auto C = mul(A,b);
cout << C.back();//第一位比较特殊,不用补位
for(int i = C.size() - 2;i >= 0;i--)
printf("%04d",C[i]);//后面的不满4位要补位
cout << endl;
return 0;
} 来看一下压位和不压位的区别,看看能快上多少毫秒(ms)
高精度乘以高精度
核心思路
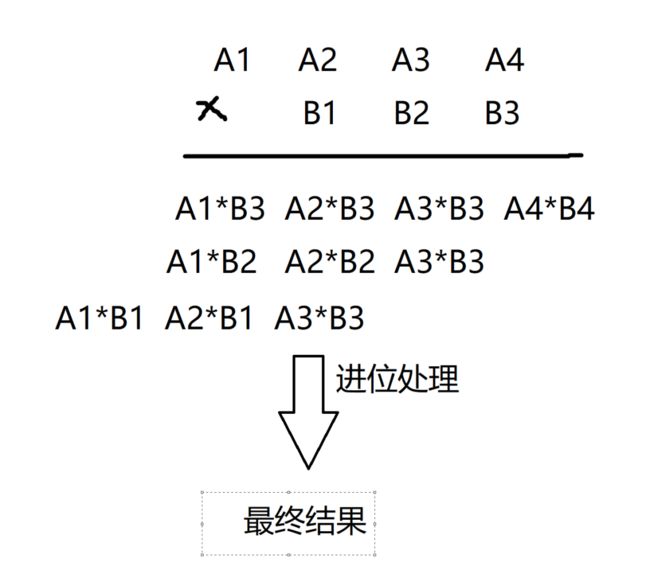
高精度乘以高精度的思路和高精度乘以低精度完全不一样。高精度乘以高精度就是模拟人工乘法,竖式乘法,然后分别相加
这样还是有点抽象,还是举个例子吧!!!
总之就分为两步,这两个数的每一位数交叉相乘,之后把对应的位数上面的数字加上,最后统一处理进位,就能得到结果了。
不压位模板
vector mul(vector A, vector B)
{
vector C(A.size() + B.size());//定义结果大小
//利用双层for循环,让每一位数交叉相乘
for (int i = 0; i < A.size(); i ++ )
for (int j = 0; j < B.size(); j ++ )
C[i + j] += A[i] * B[j];//得到每一位交叉相乘的结果
//统一处理进位
for (int i = 0, t = 0; i < C.size() || t; i ++ )
{
t += C[i];
if (i >= C.size()) //如果将要输出的位数比定义的多,就添加在末尾
C.push_back(t % 10);
else //否则,就在原位上改变数字就可以了
C[i] = t % 10;
t /= 10;
}
while (C.size() > 1 && !C.back()) //去除前导零
C.pop_back();
return C;
} 压四位模板
vector mul(vector &A,vector &B)
{
vector C(A.size() + B.size());//定义容器C大小
for(int i = 0;i < A.size();i++)
{
for(int j = 0;j < B.size();j++)
C[i+j] += A[i] * B[j] ;//A和B的每一位数相乘
}
//统一处理进位
//把后面的if语句和for循环合并了
for(int i = 0,t = 0;i < C.size() || t;i++)
{
t += C[i];
if(i > C.size())//如果进位还有数据,添加到末尾
C.push_back(t % N);
else//如果此时的位数在容器范围里面,就直接再该位数上改就行了
C[i] = t % N;
t /= N;
}
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
} 练习
不压位代码
#include
#include
using namespace std;
vector mul(vector &A,vector &B)
{
vector C(A.size() + B.size());//定义容器C大小
for(int i = 0;i < A.size();i++)
{
for(int j = 0;j < B.size();j++)
C[i+j] += A[i] * B[j] ;//A和B的每一位数相乘
}
//统一处理进位
for(int i = 0,t = 0;i < C.size() || t;i++)
{
t += C[i];
if(i > C.size())
C.push_back(t % 10);
else
C[i] = t % 10;
t /= 10;
}
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
}
int main()
{
string a,b;
cin >> a >> b;
vector A,B;
for(int i = a.size() - 1;i >= 0;i--)
A.push_back(a[i] - '0');
for(int i = b.size() - 1;i >= 0;i--)
B.push_back(b[i] - '0');
auto C = mul(A,B);
for(int i = C.size() - 1;i >= 0;i--)
cout << C[i];
cout << endl;
return 0;
} 压四位代码
#include
#include
using namespace std;
const int N = 1e4;
vector mul(vector &A,vector &B)
{
vector C(A.size() + B.size());//定义容器C大小
for(int i = 0;i < A.size();i++)
{
for(int j = 0;j < B.size();j++)
C[i+j] += A[i] * B[j] ;//A和B的每一位数相乘
}
//统一处理进位
//把后面的if语句和for循环合并了
for(int i = 0,t = 0;i < C.size() || t;i++)
{
t += C[i];
if(i > C.size())//如果进位还有数据,添加到末尾
C.push_back(t % N);
else//如果此时的位数在容器范围里面,就直接再该位数上改就行了
C[i] = t % N;
t /= N;
}
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
}
int main()
{
string a,b;
cin >> a >> b;
vector A,B;
//压位操作,不懂的话,看看前面的加减怎么压位的
for(int i = a.size() - 1,s = 0,j = 0,t = 1;i >= 0;i--)
{
s += (a[i] - '0') * t;
t *= 10,j++;
if(j == 4 || i == 0)
{
A.push_back(s);
s = j = 0;
t = 1;
}
}
for(int i = b.size() - 1,s = 0,j = 0,t = 1;i >= 0;i--)
{
s += (b[i] - '0') * t;
t *= 10,j++;
if(j == 4 || i == 0)
{
B.push_back(s);
s = j = 0;
t = 1;
}
}
auto C = mul(A,B);
cout << C.back();//第一位特殊,不用补零
for(int i = C.size() - 2;i >= 0;i--)//后面的不满4位要补零
printf("%04d",C[i]);
cout << endl;
return 0;
} 高精度除法
高精度除法稍微有点复杂,分为高精度除以低精度、高精度除以高精度。这两个对数据的处理和输出和上面的加减乘操作都一样,不在详细写了,主要来讲一下除法的核心思路
高精度除以低精度
思路
这个除法操作和上面的乘法操作一样,把低精度的数看成一个整体,然后开始进行除法操作。还记得小时候怎么进行除法的吗?人是先找到可以除的位数,从那里往后开始除
而计算机比较呆,不会自动选择可以除的地方,不论能不能除,只能从第一位开始进行除法,从而导致有前导零的存在,所以最后要注意去除前导零。
这样的除法操作的原理还记得吗?上一个原理图
为了让它们格式统一,我们可以把第一个t1改一下
这样就可以看出商和余数的关系了吧,t[i] = (r[i-1]*10+A[i])% b;
这样你们可能还有点迷糊,下面来一个实例,让你们感受一下!!!
![]()
用代码表示是这样的
//A是被除数,b是除数,r是余数
vector div(vector &A,int b,int &r)
{
vector C;//商
r = 0;
//由于是倒序存的,都是要从高位进行运算,所以应该从容器最后一位
for(int i = A.size() - 1;i >= 0;i--)
{
r = r * 10 + A[i];//每一位的余数
C.push_back(r / b);//每一位上的商
r %= b;//每一位的余数
}
return C;
} 并不是只有这些,别忘了计算机是从第一位开始进行除法操作的,千万记得去除前导零哦。
但是商是正序存到结果容器里面的,所以要把商反转一下,再去除前导零,最后再倒序输出
reverse(C.begin(),C.end());
while(C.size() > 1 && C.back() == 0)
{
C.pop_back();
}模板
vector div(vector &A,int b,int &r)
{
vector C;//商
r = 0;//余数初始化为0
for(int i = A.size() - 1;i >= 0;i--)
{
r = r * 10 + A[i];//每一位上的数
C.push_back(r / b);//每一位商
r %= b;//余数
}
reverse(C.begin(),C.end());//商为正序,需要反转
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
} 练习
------------------------------------------------(不要着急看代码)-----------------------------------------------------
不压位代码
#include
#include
#include
using namespace std;
vector div(vector &A,int b,int &r)
{
vector C;//商
r = 0;//余数初始化为0
for(int i = A.size() - 1;i >= 0;i--)
{
r = r * 10 + A[i];//每一位上的数
C.push_back(r / b);//每一位商
r %= b;//余数
}
reverse(C.begin(),C.end());//商为正序,需要反转
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
}
int main()
{
string a;
int b,r;
cin >> a >> b;
vector A;
for(int i = a.size() - 1;i >= 0;i--)
A.push_back(a[i] - '0');
auto C = div(A,b,r);
for(int i = C.size() - 1;i >= 0;i--)
cout << C[i];
cout << endl << r << endl;
return 0;
} 压四位代码
#include
#include
#include
using namespace std;
const int N = 1e4;
vector div(vector &A,int b,int &r)
{
vector C;//商
r = 0;//余数初始化为0
for(int i = A.size() - 1;i >= 0;i--)
{
r = r * N + A[i];//每一位上的数
C.push_back(r / b);//每一位商
r %= b;//余数
}
reverse(C.begin(),C.end());//商为正序,需要反转
while(C.size() > 1 && C.back() == 0)//去除前导零
C.pop_back();
return C;
}
int main()
{
string a;
int b,r;
cin >> a >> b;
vector A;
for(int i = a.size() - 1,s = 0,j = 0,t = 1;i >= 0;i--)//压位
{
s += (a[i] - '0') * t;
t *= 10,j++;
if(i == 0 || j == 4)
{
A.push_back(s);//压进去后,记得重新初始化
s = j = 0;
t = 1;
}
}
auto C = div(A,b,r);
cout << C.back();//第一个输出不用补零
for(int i = C.size() - 2;i >= 0;i--)
printf("%04d",C[i]);//其他的不满四位都需要补零
cout << endl << r << endl;
return 0;
} 高精度除以高精度
高精度除以高精度,平时用的比较少,就暂时不说了。(主要是我现在还不会)不过可以提供一下思路,用减法模拟除法,不过效率比较慢。
五、前缀和与差分
前缀和
介绍+思路
前缀和,是给定一个数组a1、a2、a3、a4、...ai,然后前缀和就是原数组中前i个数之和,就是高中数列的前n项和,只不过不是等差数列、等比数列。
其次,我们需要知道第 i 项和前 i - 1 项和的关系。S[i] = S[i - 1] + a[i]这个应该可以理解吧。换个高中公式,就是Sn-Sn-1 = an。这下应该明白了吧。知道了上面的那个公式,我们可以干什么啊?当然是把给前缀和数组赋值。不再需要使用for循环以O(n)的时间复杂度求前缀和了;而是O(1),更加快速方便。
注意:给前缀和数组赋值时,需要从1开始,而不是0。为什么呢?当 i 等于0时,S[0]=S[-1] + a[0]。这样就会越界访问了,所以要从1开始,并且令S[0] = 0(当全局变量定义前缀和数组时,默认每一项都为零)
最后有了前缀和数组怎么求区间和呢?很简单的,就一个公式,区间l,r的前缀和为s[r] - s[l - 1]。大家可能有点诱惑,接下来看这张图片,你就明白了
详细地写出来了S[l]、S[r] 、[l,r]的区间和,应该可以看得出规律吧!
[l,r]的区间和 = S[r] - S[l - 1]
So,你get到了吗?
模板
#include
using namespace std;
const int N = 1e5 + 10;
int nums[N],s[N];//nums数组为原数组,s数组为前缀和数组
int n;//元素个数
int main()
{
for(int i = 1;i <= n;i++)
cin >> nums[i];
for(int i = 1;i <= n;i++)
s[i] = s[i - 1] + a[i];//处理前缀和数组
//接下来就是你想要询问的区间和的操作了,不再具体写了
//区间和公式:l~r的区间和 = s[r] - s[l - 1];
} 练习
传送阵:795. 前缀和 - AcWing题库
这个和上面讲的模板一样吧,就直接套板子吧!
#include
using namespace std;
const int N = 1e5 + 10;
int nums[N],s[N];//原数组和前缀和数组
int main()
{
int n,m;
cin >> n >> m;
for(int i = 1;i <= n;i++)//下标从1开始存入原数组
cin >> nums[i];
for(int i = 1;i <= n;i++)//给前缀和数组赋值
s[i] = s[i - 1] + nums[i];
while(m--)
{
int l,r;
cin >> l >> r;
cout << s[r] - s[l - 1] << endl;//公式
}
return 0;
} 扩展
掌握了求一维数组的前缀和的方法后,来看看二维数组的前缀和怎么求吧!
思路
二维数组的前缀和的核心也是两个公式,一个是给前缀和数组赋值的,另一个就是求一部分二维数组的前缀和了。只不过公式与一维数组有所不同而已!
下面这是一个二维数组,让我们用这个数组来讲解一下知识点
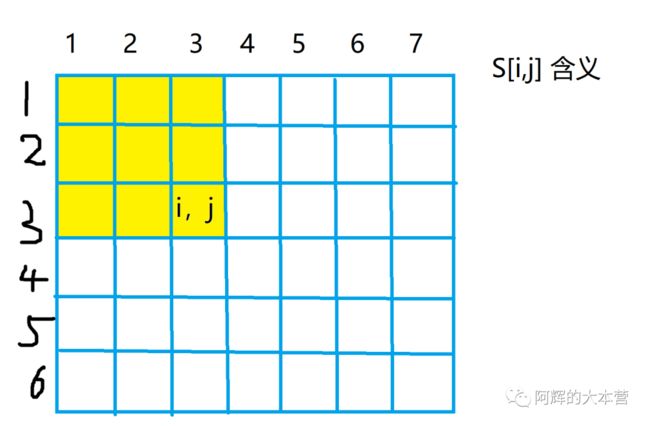
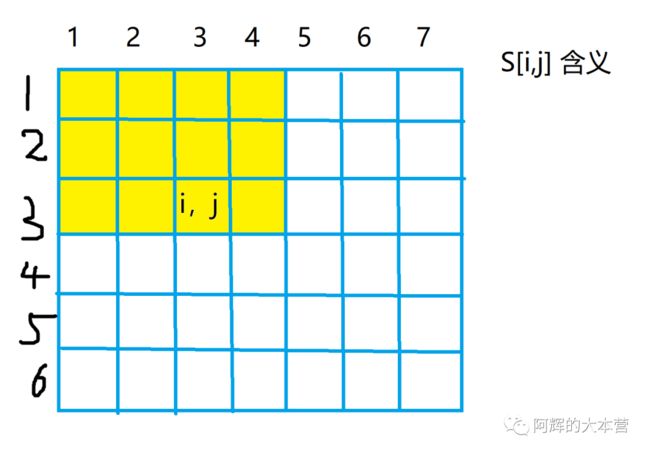
首先,我们需要知道S[i,j]表示什么,是哪些的和?
这时候,上面黄色块的和为S[3,3]。那么S[3,4]表示哪些的和呢?
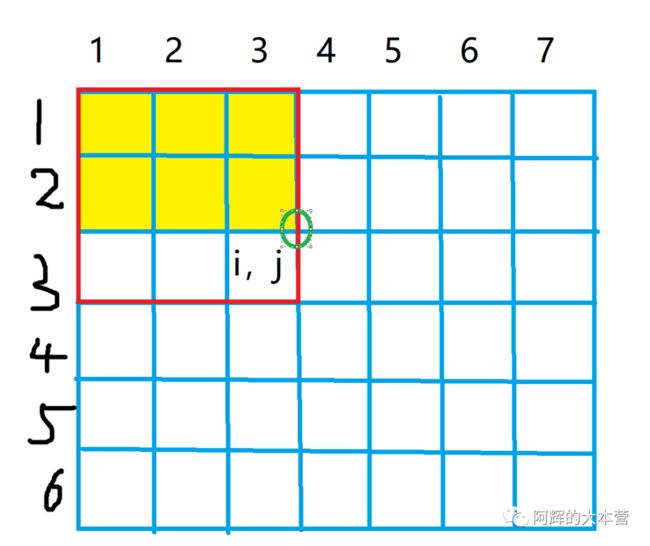
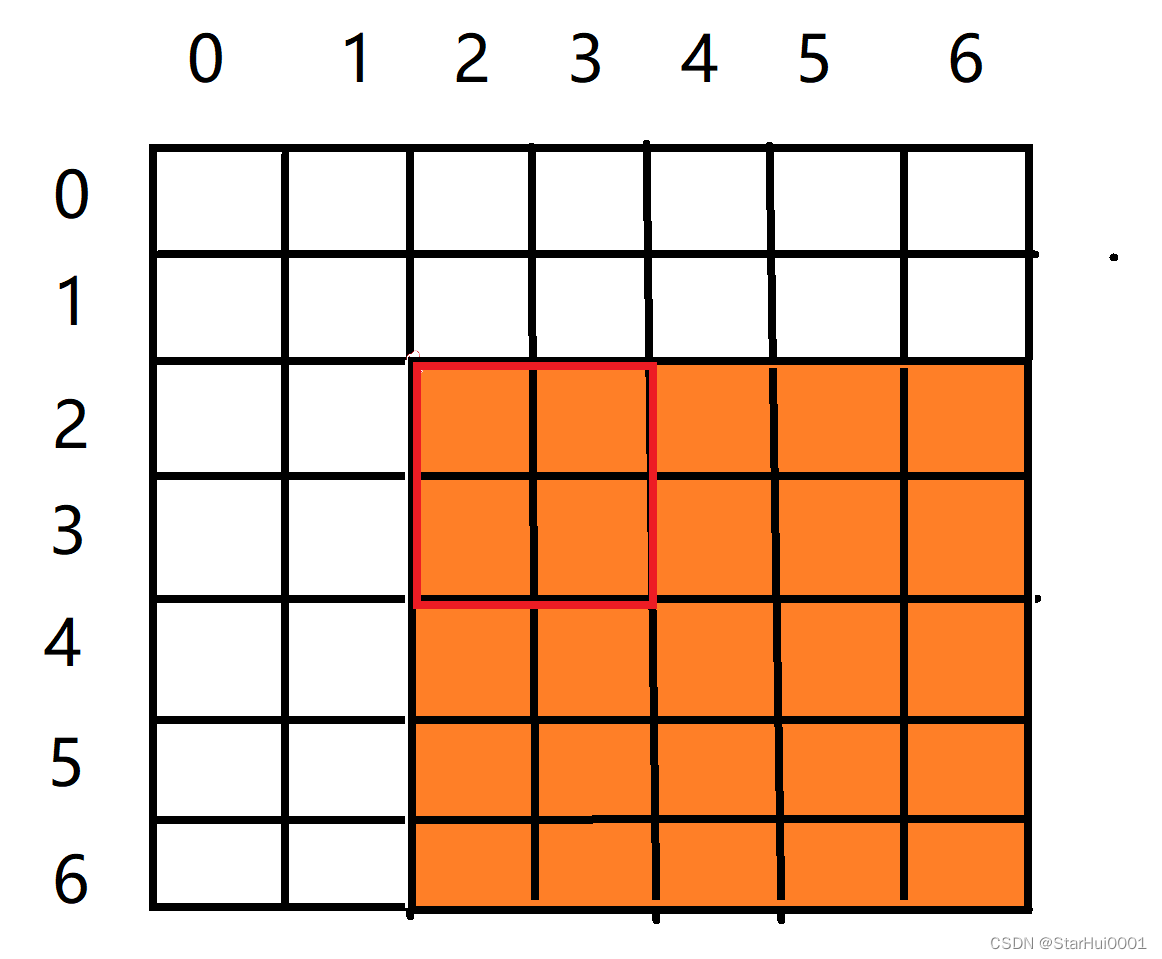
所以懂了吗?S[i,j]表示i行j列的数字之和。那么S[i,j]是如何计算的呢?
其实它有一个公式S[i,j] = S[i - 1,j] + S[i,j - 1] - S[ i-1 ,j - 1] + a[i,j];下面我来演示一下怎么搞的
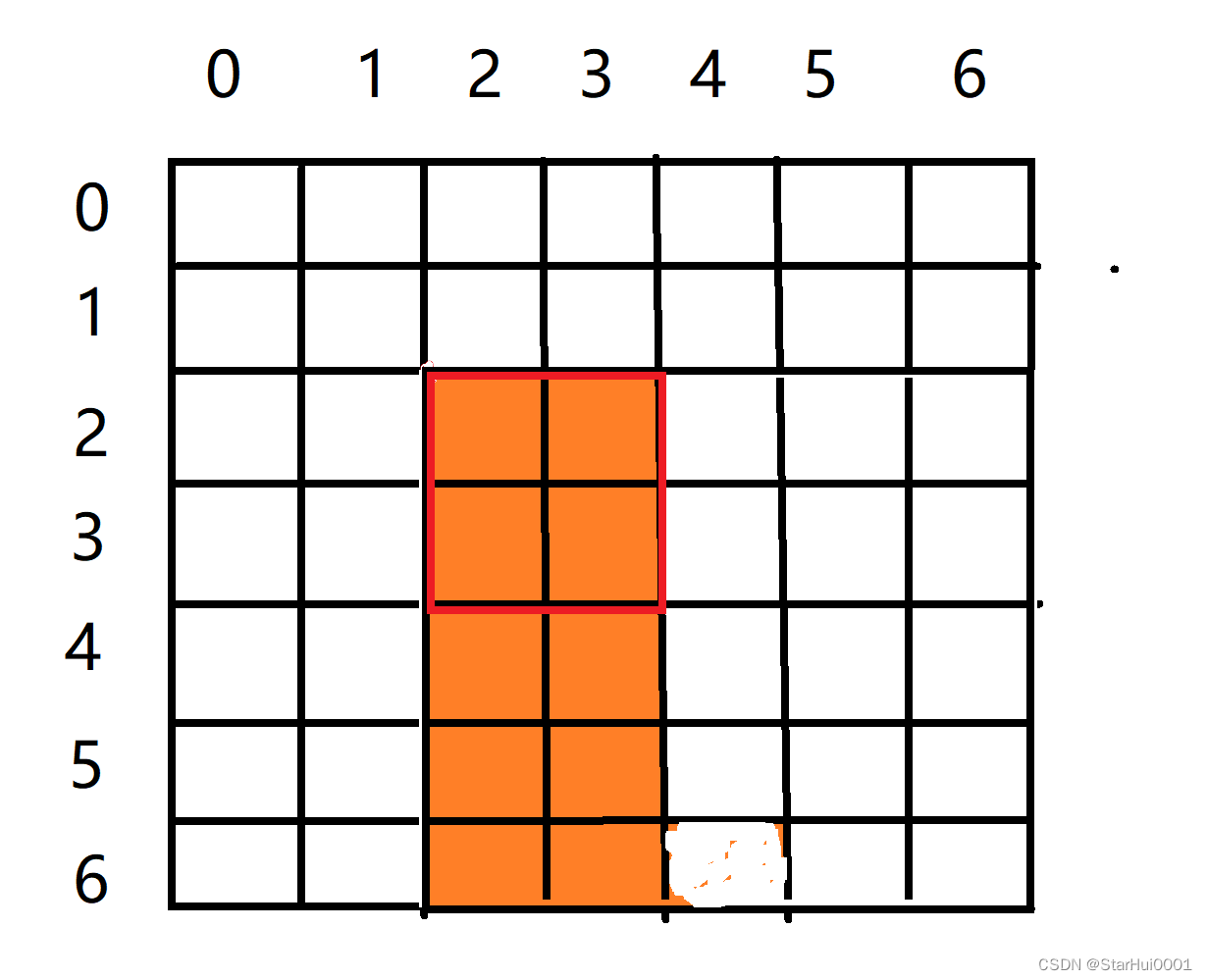
S[i - 1,j]就是这个a[i,j]的右上角到二维数组左上角围成的面积
S[i,j - 1]就是a[i,j]的左下角与二维数组的左上角围成的面积
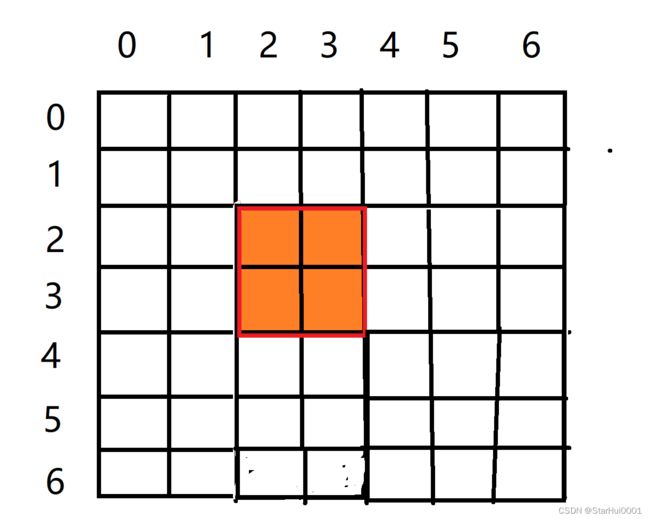
S[i - 1,j - 1]就是a[i,j]的左上角与二维数组左上角围成的面积
所以,你理解这个公式了吗?之所以减去S[i-1,j - 1]是因为加了两遍。
下面最最最核心的来了,就是子矩阵的求和,有了左上角(x1,y1)和右下角(x2,y2)的坐标,求子矩阵的和就是一个公式而已。
子矩阵的和=S[x2,y2] - S[x1 - 1,y2] - S[x2,y1 - 1] + S[x1 - 1,y1 - 1]
可能还是有一点抽象,大家看一下y总的讲解吧!
前缀和公式讲解
练习
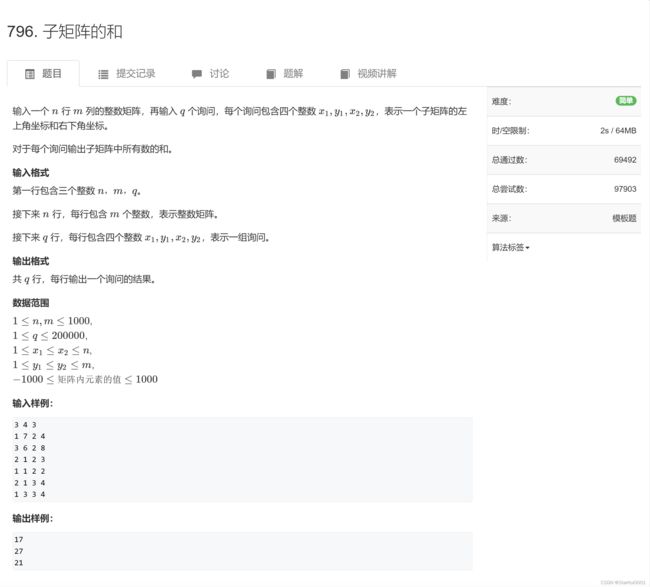
传送阵:796. 子矩阵的和 - AcWing题库
-----------------------------------------------------------代码分割线-------------------------------------------------------
#include
using namespace std;
const int N = 1010;
int s[N][N];
int main()
{
int n,m,q;
cin >> n >> m >> q;
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{ scanf("%d",&s[i][j]);//读取数据,并给二维数组赋值
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];//公式
}
}
int x1,x2,y1,y2;
while(q--)
{
cin >> x1 >> y1 >> x2 >> y2;
int res = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];//公式
cout << res << endl;
}
return 0;
} 差分
介绍 + 思路
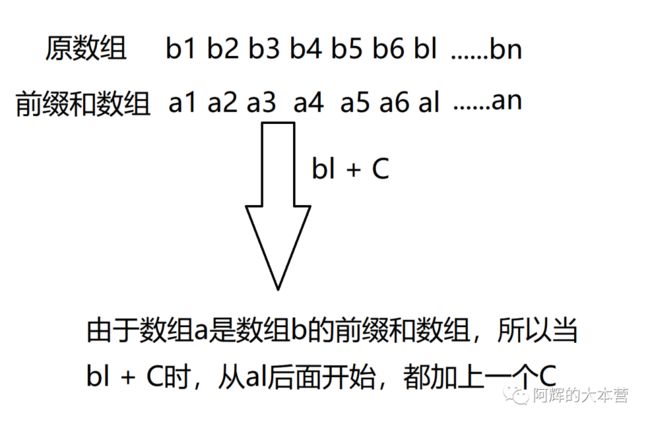
有一个原始数列a1 、a2、a3 ......an,构造一个新数列b1、b2......bn,使得ai = b1 + b2 +... + bi,使得ai是数列b的前缀和,b是a的差分,是前缀和的逆运算 。
差分的应用主要是解决一种操作:给定一个区间[l,r],把A数组里面这些区间全部加上一个C,只需要在B数组修改两个数就可以了
这两个数是B[ l ] +C,B[ r + 1 ] - C。为什么呢?
B[ l ] + C会导致,从前缀和数组A[ l ]开始,每一个前缀和数组都加上C(因为al及以后的数组元素求和时会加上bl,而bl又加上了C)。
而我们只是想让前缀和数组a [ l ,r ]区间里面的元素加上C,所以需要进行的操作是 B[r + 1] - C;和上面同理。
![]()
但是有的人可能不会构造差分数组,其实不需要构造差分数组。只需要把差分数组看成全为0的数组。但是前缀和数组有数啊,差分数组却为0,肯定不对啊!!!所以就对差分数组进行插入操作,这样就可以和前缀和数组对应上了。
步骤
1、构建差分数组
构建差分数组,不需要我们想,就利用前缀和数组来进行构建。那怎么构建呢?
我们把前缀和数组的值想象成是在数值为0的差分数组上进行插入操作的,利用前缀和数组逆向构建差分数组。
for(int i = 1;i <= n;i++)
{
cin >> a[i];
insert(i,i,a[i]);
}而insert函数就是我们上面提到的插入操作,具体逻辑请看代码
void insert(int l,int r,int c)
{
b[l] += c;
b[r + 1] -= c;
}这样就保持了只在区间为[l,r]上加上常数。
2、插入操作
就是上面的插入函数,在给定的区间上的每个数加上常数。
练习
传送阵:797. 差分 - AcWing题库
-----------------------------------------------------------代码分割线-------------------------------------------------------
#include
using namespace std;
const int N = 1e5 + 10;
int a[N],b[N];//数组a为前缀和数组,数组b为差分数组
//插入操作
void insert(int l,int r,int c)
{
b[l] += c;//从l开始都加上常数C
b[r + 1] -= c;//从r + 1开始都减去常数C
//这样保持了只把区间[l,r]加上常数C,其他区间都不变
}
int main()
{
int n,m;
cin >> n >> m;
for(int i = 1;i <= n;i++)
{
cin >> a[i];
insert(i,i,a[i]);//给差分数组赋值
}
while(m--)
{
int l,r,c;
cin >> l >> r >> c;
insert(l,r,c);//在差分数组进行插入操作
}
for(int i = 1;i <= n;i++)
{
a[i] = a[i - 1] + b[i];//前缀和求和
cout << a[i] << ' ';
}
return 0;
} 扩展
学习了一维数组的差分,来学习二维数组的差分吧!
思路
一维数组的差分是构造一个数组使得是原数组的前缀和,二维数组的差分也是如此。构造一个二维数组使得是原数组的前缀和。
核心:给定一个数组a[ i ][ j ],构造差分矩阵,使得a[ ][ ]是 b[ ] [ ]的二维前缀和。但是我们不需要构造差分数组,只需要把原数组看成全是0的数组,然后通过核心操作构建出来
核心操作:给以(x1,y1)为左上角、(x2,y2)为右上角的子矩阵中所以的数a[ i , j ]都加上C
S[ 2,2 ]表示为(2,2)与右下角围成的面积
对于差分数组的影响:S[ x1, y1 ] += C;
S[x1, y2 + 1] -= C;
S[ x2 + 1,y1] -= C;
S[x2 + 1,y2 + 1] += C;
二维数组差分
模板
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
举例
如果我们想让以(2,2)为左上角、(4,4)为右下角的子矩阵加上常数C,看模板。
首先把(x1,y1)加上C,所以这个数及其后的数组的前缀和都被加上常数C,就是(2,2)加上常数C
然后再把(x2+1,y1)减去常数C,就是(5,2)减去常数C。
之后是(x1+1,y2)减去常数C,也就是(1,5)减去常数C
(黑色的表示,被减去常数C)
最后(x2+1,y2+1)加上常数C
这样就完成对一个区间加上常数C。
练习
传送阵:798. 差分矩阵 - AcWing题库
#include
using namespace std;
const int N = 1010;
int a[N][N],b[N][N];
int n,m,q;
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
cin >> n >> m >> q;
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
scanf("%d",&a[i][j]);
insert(i,j,i,j,a[i][j]);//二维差分数组
}
}
while(q--)
{
int x1,y1,x2,y2,c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1,y1,x2,y2,c);
}
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];//二维数组的前缀和
printf("%d ",b[i][j]);
}
cout << endl;
}
return 0;
}
六、双指针算法
介绍
双指针算法通过设置两个指针不断进行单向移动来解决问题的方法。
它包含两种形式
1、两个指针分别指向不同的序列。比如:归并排序的合并过程。
2、两个指针指向同一个序列。比如:快速排序的划分过程。
双指针算法的核心思想就是优化时间复杂度。
本来是双层for循环,O(n²)的时间复杂度。通过双指针算法可以优化到O(n)的时间复杂度。那是如何优化的时间复杂度呢?其实是当一个指针满足条件后才会单向移动,没有指针的回溯,而每次都会有指针的移动。
双指针算法的模板大致都是下面这样
for(int i = 0,j = 0;i < n;i++)
{
while(j < i && check(j))//当j指针满足一一定条件后才会移动
j++;
// 每道题的具体逻辑
}示例
给大家举一个最简单的应用。让一个由单词组成的字符串,按照单词输出,一个单词占一行。例如让 Life is but a hard and tortuous journey里面的一个单词一行输出
如果使用双层for循环的话,比较慢。这是用双指针算法来优化
逻辑很简单,就是i指针在每一个单词第一个位置,
然后j指针开始往后移,直到遇到空格停止,
然后更新i指针
代码如下
#include
#include
using namespace std;
int main()
{
char a[1010];
cin.get(a,1010);//读入字符串,gets函数已经被删除了
int len = strlen(a);
for(int i = 0;i < len;i++)
{
int j = i;
while(j < len && a[j] != ' ')//满足某种性质,当j指针停的时候,已经走到了空格
j++;
for(int k = i;k < j;k++)//这时候打印i到j - 1之间得到字符
cout << a[k];
cout << endl;
i = j;//更新指针,跳过空格
}
return 0;
} 而怎么才能写出双指针算法的代码呢?不可能直接写出来啊,应该先写出暴力做法,再看看i和j有什么联系,然后利用这些联系进行优化。
还是一句话:勤加练习,熟能生巧,练的多了就直接能写出双指针算法的代码!!!
应用1(最长连续不重复子序列)
传送门:799. 最长连续不重复子序列 - AcWing题库
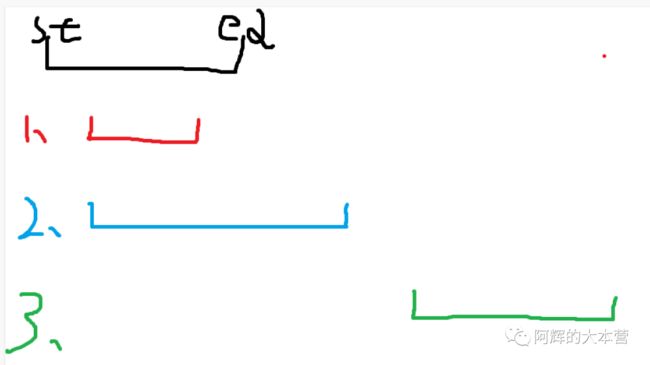
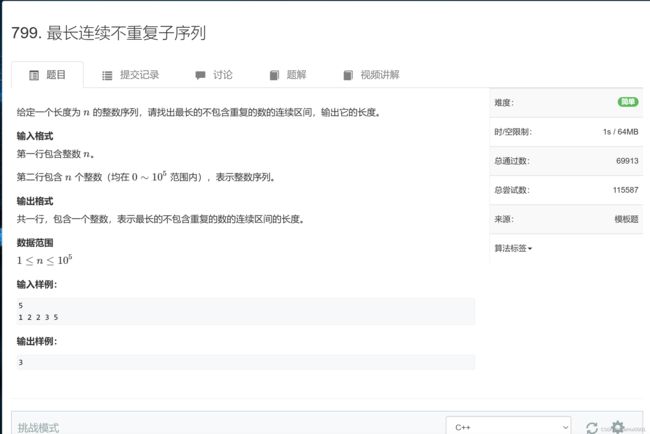 思路
思路
暴力做法
暴力做法就是使用两个for循环遍历数组,i为序列起点,j为序列终点,然后对这个序列进行判断。而判断这个序列是否有重复元素时,又需要for循环遍历一遍,所以时间复杂度是O(n³)。
双指针算法进行优化
其实用双指针算法优化也是比较简单的,就是使用两个指针。
一个指针i是遍历的,是子序列的终点;而另一个指针j是子序列的起点。而我们只需要判断这个子序列里面是否有重复元素,如果有重复元素的话,就把表示子序列起点的指针右移,直到没有重复元素为止。
而怎样进行重复元素的判断呢?此时我们可以开一个次数数组,记录每个元素出现的次数,当子序列的右端点右移时,次数数组对应的位置就加1,;相反,当左端点右移时,对应的位置就减1。
模拟
上实例,帮助你们理解一下
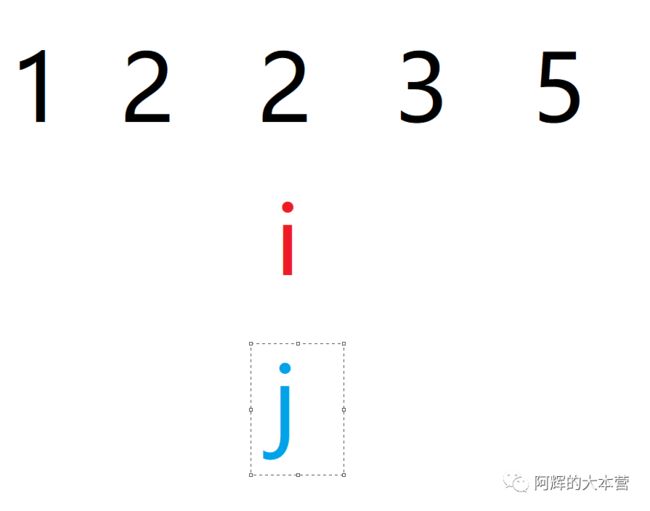
就拿1、2、2、3、5举例子吧。
刚开始都从第一个数开始
i指针继续遍历,直到走到重复元素那里。
这时候,我们通过开的次数数组已经知道该子序列有重复元素了。所以就需要把子序列的左端点右移,直到没有重复元素为止,然后i指针继续往右走
这时候没有重复元素了,i指针继续往右走。走到末尾,没有重复元素了
此时 i - j + 1,就表示该子序列的元素个数。(i为右端点,j为左端点)
这样子应该能理解了吧!!!
代码
#include
using namespace std;
const int N = 1e5 + 10;
int a[N],s[N];//数组s存储的是数组元素出现的次数
int main()
{
int n;
cin >> n;
for(int i = 0;i < n;i++)
cin >> a[i];
int res = 0;//结果
for(int i = 0,j = 0;i < n;i++)
{
s[a[i]]++;//每遍历一个元素,次数数组s对应的位置就加一,表示出现一次
//j < i 表示子序列里面有元素,且a[i]出现多次,所以就把左端点右移
while(j < i && s[a[i]] > 1)
{
s[a[j]]--;//表示子序列的左端点往右移,且左端点的次数减1
j++;
}
res = max(res,i - j + 1);//结果
}
cout << res << endl;
return 0;
} 应用2(数组元素的目标和)
传送门:800. 数组元素的目标和 - AcWing题库
思路
这一题其实是一个很典型的双指针算法的应用。就是使用两个指针 i 和 j。i指针从一个数组头开始走,j指针从另一个指针末尾开始走。如果两者相加大于目标值的,j指针往左走,直到和小于等于目标值位置。然后判断是否与目标值相等,如果相等,就输出。
代码
#include
using namespace std;
const int N = 1e5;
int a[N],b[N];
int main()
{
int n,m,x;
cin >> n >> m >> x;
for(int i = 0;i < n;i++)
cin >> a[i];
for(int i = 0;i < m;i++)
cin >> b[i];
for(int i = 0,j = m - 1;i < n;i++)//典型的双指针算法模板
{
while(j >= 0 && a[i] + b[j] > x)//控制j指针往左走的条件
j--;
if(a[i] + b[j] == x)//如果j指针停下的时候,刚好之和等于目标值,就输出
{
cout << i << ' ' << j;
break;
}
}
return 0;
} 应用3(判断子序列)
传送门:2816. 判断子序列 - AcWing题库
思路
模拟
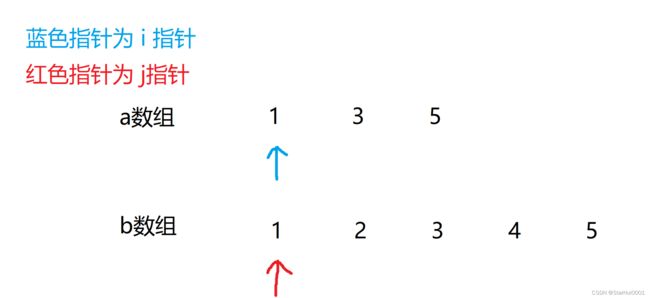
就拿题目给的例子吧,a数组为1、3、5,b数组为1、2、3、4、5
首先匹配a数组的第一个元素,第一个元素匹配成功,i 、 j指针都往后移
a数组进行第二个元素的匹配,不成功,i 指针不动,j 指针往后移
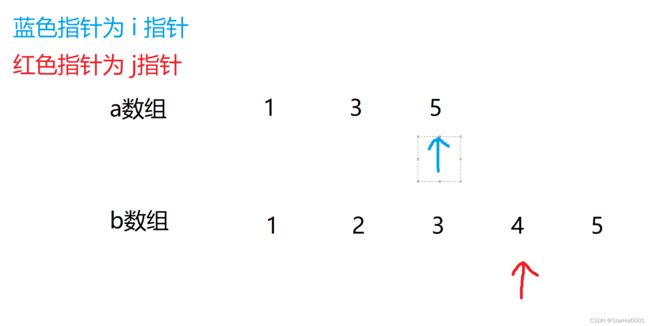
再次进行a数组第二个元素的匹配,匹配成功;i 、j 指针都往后移
a数组第三个元素第一次匹配不成功,i 指针不动,j 指针往后移;准备进行第二次匹配
第三次匹配成功,i 指针已经指向了 a数组最后一个元素,循环结束
代码
#include
#include
using namespace std;
const int N = 100010;
int a[N],b[N];
int main()
{
int n,m;
cin >> n >> m;
for(int i = 0;i < n;i++)
scanf("%d",&a[i]);
for(int i = 0;i < m;i++)
scanf("%d",&b[i]);
int i = 0,j = 0;
while(i < n && j < m)//循环条件,不能越界访问数组
{
if(a[i] == b[j])//第一次是用来判断两个数组的首元素是否相等,后面判断第n个数字是否相等
i++;
j++;//无论是否相等都要j++,因为要遍历b数组
}
if(i == n)//如果i等于n的话,就证明匹配上了
puts("Yes");
else
puts("No");
return 0;
}
七、位运算
位运算的话,只是介绍几种最常见的操作!!!
在开始之前,大家要了解几种位运算符,位运算_百度百科 (baidu.com)
常用操作1:整数的第k位数(二进制)
介绍
这个操作是为了求 整数 x (十进制)的 第 k 位数是0 / 1(二进制)
原理
1、先把第k位移到最后一位,x >> k,用位移运算
2、看个位是几,x & 1(位运算&,只有两个1&时,才会返回1;否则返回0)
公式: (x >> k) & 1
常用操作2:返回整数的最后一位1
介绍
lowbit(x)函数
作用:返回x的最后一位1(二进制下的)
比如:x = 1010(二进制),lowbit(x) = 10(二进制) = 2(十进制)
x = 101000(二进制),lowbit(x) = 1000(二进制) = 8(十进制)
原理
在C++里面,一个数的负数等于原数的补码,补码又等于 取反(~)+ 1
不理解补码的可以看看补码_百度百科 (baidu.com)。
使用 x & -x 等价于 x & (~x + 1)
&运算符应该都知道吧,只有对应的数为1时结果为1,否则都是0
公式:x & ( - x)
应用(二进制中1的个数)
传送门:801. 二进制中1的个数 - AcWing题库
思路
这个题是让我们统计二进制中1的个数,由上面讲的常用操作可以求出最后一位1,我们求出来最后一位后 就减去,直到这个数等于0为止,开一个计数器统计减去的次数,这样就可以得到1的个数了。
代码
#include
using namespace std;
int n;
int lowbit(int x)
{
return x & -x;
}
int main()
{
cin >> n;
while(n--)
{
int a,res = 0;
cin >> a;
while(a)
{
a -= lowbit(a);//减去返回的最后一位1
res++;//计数器
}
printf("%d ",res);
}
return 0;
} 八、离散化
介绍
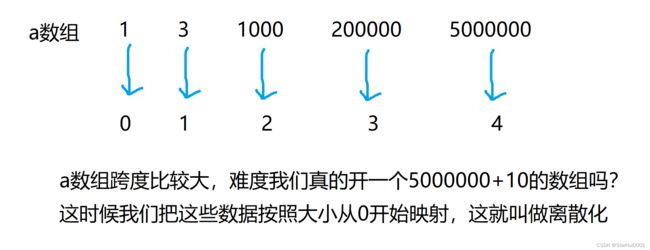
离散化,把无限空间的有限的个体映射到有限的空间中去,以此提高算法的时空效率。通俗的说,离散化是在不改变数据相对大小的条件下,对数据进行相应的缩小。核心是整个区间跨度很大,但是用到数据不是很多,比较稀疏。
问题
问题1:数组可能有重复元素
数组如果有重复元素的话,我们离散化的时候就会出现重复的,所以我们应该去重。由于离散化是有序的,所以我们再去重之前应该先排序。
排序的话,调用C++库函数sort函数就可以了。去重推荐也是推荐使用库函数
解决代码
vector alls;//存储所有离散化的值
sort(alls.begin(),alls.end());//排序
all.erase(unique(alls.begin(),alls.end()),all.end())//去除重复元素
解惑
1、sort(start,end,cmp)函数是C++头文件为#include
有三个参数,第一个是start排序数组的起始地址,第二个end是数组结束地址的下一位;第三cmp用于规定排序的方法,可不填,默认升序。sort函数_百度百科 (baidu.com)
2、upique(start,end)函数是C++头文件#include
3、erase()函数,有两种用法,一是c.erase(p)删除迭代器p所指向的元素。二是c.erase(start,end)删除迭代器start到end区域内的元素。
c为容器对象,返回值都是迭代器,该迭代器指向被删除元素的后面的元素。
c++学习之容器——erase()函数_qingtianweichong的博客-CSDN博客
问题2:如何找到离散化后的对应的值
当我们把一个整数x离散化后,如何找到离散化后的值呢?
其实很简单,想一想我们之前学过的查找方法,它就是整数的二分查找。
忘记的话大家自行回顾哦!
解决的代码
//二分求出x对应的离散化的值
int find(int x)//找到第一个大于等于x的位置
{
int l = 0,r = all.size() - 1;
while(l < r)
{
int mid = l + r >> 1;
if(alls[mid] >= x)
r = mid;
else
l = mid + 1;
}
return r + 1;//映射到1,2.....n;或者是return r;映射到0,1,2,....n - 1;
}
应用:区间和
传送门:802. 区间和 - AcWing题库
思路
这一道题是让我们求一个值域大、稀疏的数组的区间和,自然是需要进行离散化了。由于离散化的值比较难找,所以还需要用到二分查找。当然了,求区间和必须得用到前缀和啊!!!
整理一下,就是 离散化 + 二分查找 + 前缀和
这些知识点我都讲过,翻一下上面的内容,复习后再来做题。
代码
#include
#include
#include
using namespace std;
typedef pair PII;
const int N = 300010;
int a[N],s[N];//数组a是存储离散化后的值,s是前缀和数组
vector alls;//待离散化的数据
vector add,query;//储存插入、询问的数组
int find(int x)
{
int l = 0,r = alls.size() - 1;
while(l < r)
{
int mid = l + r >> 1;
if(alls[mid] >= x)//找到第一个大于等于x的
r = mid;
else
l = mid + 1;
}
return r + 1;//返回r+1,照顾了下面的前缀和运算,不用处理边界问题
}
int main()
{
int n,m;
cin >> n >> m;
for(int i = 0;i < n;i++)
{
int x,c;
cin >> x >> c;
add.push_back({x,c});
alls.push_back(x);//把x存到待离散化的数组
}
for(int i = 0;i < m;i++)
{
int l,r;
cin >> l >> r;
query.push_back({l,r});
alls.push_back(l);//把左右区间存到待离散化的数组
alls.push_back(r);
}
//经过处理,所以待离散化的数据已经存储到待离散化的数组
// 排序去重
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());
//处理插入
for(auto item : add)//遍历add,并赋值给item
{
int x = find(item.first);//得到插入点离散化后的值
a[x] += item.second;//把插入的数组存到数组a
}
// 预处理前缀和
for(int i = 1;i <= alls.size();i++)
{
s[i] = s[i - 1] + a[i];//前缀和公式
}
for(auto item : query)
{
int l = find(item.first),r = find(item.second);//依次得到左右区间离散化后的值
cout << s[r] - s[l - 1] << endl;//前缀和公式
}
return 0;
}
九、区间合并
传送门:803. 区间合并 - AcWing题库
思路
先来说一下区间合并,区间合并是合并那些有交集的区间,没有交集就合并不了,就是另一个新的区间。
区间合并,肯定要有区间,就肯定有左右端点,那用什么存储左右端点呢?pair还是比较合适的。存储之后,就可以进行排序了!对每一个线段的左端点从小到大进行排序,刚好sort函数对pair类型刚好可以先排序左端点,再排序右端点!然后定义一个起始维护区间(负无穷到负无穷,看数据范围定义)。开始遍历每一个线段1,如果线段的左端点大于维护区间的右端点,说明并不存在交集那么这个线段就是一个新区间,就会变成一个新的维护区间。反之线段的左端点小于维护区间的右端点,就需要对线段的右端点和维护区间的右端点进行比较,保证新的维护区间的右端点是这两个端点中最大的。
步骤
-
对线段的左右端点进行排序
-
扫描所有线段,把所有相交的线段合并
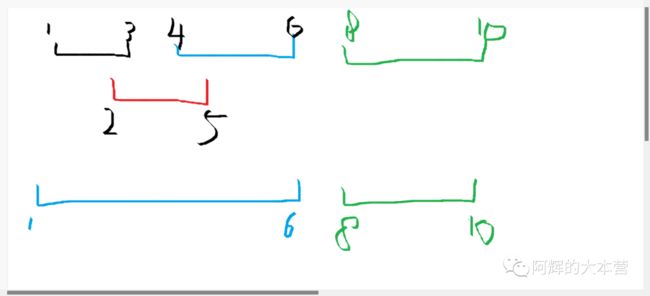
这时有三种情况:a、被包含维护区间里面
b、与维护区间有交集
c、比前面的维护区间大,没有交集
三种情况对应下面的1、2、3线段
合并后的情况:
a、维护区间不变
b、维护区间的左端点不变,右端点变大
c、上一个维护区间结束,换一个新的维护区间
三种情况对应下面的1、2、3线段(代码里面a、b化为一种情况)
代码
#include
#include
#include
using namespace std;
typedef pair PII;
vector segs;
void merge(vector &segs)
{
vector res;//存储结果
sort(segs.begin(),segs.end());//pair的排序:优先排序左端点,再排序右端点
int st = -2e9,ed = -2e9;//根据数据范围,定义一个需要维护的边界
for(auto seg : segs)//从前到后扫描所有的线段
{
if(ed < seg.first)//需要维护的区间的右端点小于线段的左端点
{
//加判断语句是为了特殊处理第一个区间
if(st != -2e9)//这时候已经找到了一个新区间,但是需要判断一下,不能是初始的维护区间
res.push_back({st,ed});
st = seg.first,ed = seg.second;//此时维护区间变成第一个线段的区间
}
else//说明线段与维护区间有交集,需要比较维护区间的右端点和线段的右端点
ed = max(ed,seg.second);
}
//把最后的区间加到答案里面,进行判断是为了反正输入的segs是空区间
//如果不加,当输入区间为空时,返回的区间为1,当题目明确不能输入空区间,这是可以省略
if(st != -2e9)
res.push_back({st,ed});
segs = res;
}
int main()
{
int n;
cin >> n;
while(n--)
{
int l,r;
cin >> l >> r;
segs.push_back({l,r});//存储左右区间
}
merge(segs);
cout << segs.size() << endl;//区间个数就是segs的大小
return 0;
} 赠y总模板
void merge(vector &segs)
{
//在这个函数外面还有一个typedef pair PII
// 这样可以理解这个res了吧
vector res;
// 左右端点排序
sort(segs.begin(), segs.end());
// 定义一个起始维护区间
int st = -2e9, ed = -2e9;
// 遍历有两种大情况,一个是有交集(包含或有共同部分),一个是没交集
for (auto seg : segs)
if (ed < seg.first)// 没交集,说明是新区间
{
if (st != -2e9) res.push_back({st, ed});//把新区间存到结果
st = seg.first, ed = seg.second;//更新维护区间
}
else ed = max(ed, seg.second);
// 有交集,把合并后的区间的右端点更新为最大有端点
//判断输入segs是否为区间
if (st != -2e9) res.push_back({st, ed});
segs = res;//把结果给segs,方便后面用segs的大小表示区间个数
} 结束语
实在是不好意思,之前忘了博客这个事情了,整天都在忙着写公众号文章,大家有兴趣的可以看看我的公众号(就是图片上的水印名字)。
之后会进行第二讲的更新的,谢谢大家的支持和陪伴!!!