【密码学】北航公开课《密码的奥秘》笔记
课程链接:
【【公开课】北京航空航天大学:密码的奥秘】
注1:本章内容仅用于记录个人收获,如有误,为个人理解出现偏误,望指正。
注2:本章内容更像是一个密码学导论,仅作 Introduction 的 作用。
第一讲 密码的起源
(该部分内容均为纯个人见解,正误性有待商榷,请慎重读取。)
- 一切信息内容的传递形式都可以从某种程度上视为“密码“
- 密码 的形式:即映射、hash。 将 抽象、非抽象的信息,映射为文字、图画等。
- 密码 的本质:使用信息发送方和信息接收方可以理解,而其他任意第三方无法理解或难以理解的语言形式,传递信息。
- 密码 的目的:秘密传递信息。控制信息可知范围。
注:第1点的补充例子
三个人在一起,两个人会说方言,另一个听不懂方言,那么这两个人如果有悄悄话要说,那么方言便成为了这个场合中的一种密码。
第二讲 古典密码(※)
一、 前置定义:
明文 :加密之前的、人可以直接阅读理解的文字
密文:加密之后的,人难以直接理解的文字
密钥:可以将密文和明文进行相互转化的 关键钥匙。
二、 古典密码的两大基本方法:
- 置换密码 :不更改字母(不更改语言)只更改文字顺序。
- 代换密码 :将明文字母,单表代换、多表代换、多字母代换。
三、凯撒密码(单表代换密码)
加密方式:
将每个字母按字母表顺序后推(前移)k位
例:
明文: students
密钥:后移3位
密文:vwxghqwv
优点: 加密方式简单
缺点: 容易被穷举法破译;且语言已知,容易识别
四、维吉尼亚密码(多表代换密码)
加密方式
(查表法,或 加和取模法)
给定密钥串 key,明文串str,将key重复写若干次,使key串与str串等长。得下列形式。将对应位加和并取模得密文。
例:
明文: 0 1 2 3 4 5
密钥: 0 1 2, 模 5
key: 0 1 2 0 1 2
密文: 0 1 4 3 0 2
注: 字母串同理。
优点: 相对复杂,相同的明文字母可能对应多个密文字母。
缺点: 如果密钥足够长,期间就会出现大量重复密文序列,通过计算重复密文序列间的公因子,分析者可精确计算密钥长度。
五、普莱费尔密码(多字母代换)
加密方式:
part1. 密钥表 制作规则
绘制 5*5 的方格表,后续将所有的 i 和 j 视为同一个字母。(26个字母,正好25个格子)
给定密钥单词,将密钥单词中的字母按单词中出现的顺序(重复字母只填入一次)依次填入表格;
表格中剩余位置,按字典序将其余字母依次填入。
part2. 密钥表 使用规则
step1. 明文串 分组
先将明文中所有的 J 和 I 都用 I表示
(两两分组)然后将明文串中的相邻字符进行两两分组。
(组内字母不同)如果某一组中的两个字母为同一字母,则在其中插入随机无效字母,然后重新分组。
(组内字母都为两个)如果串长为奇数,则补无效字母到最后一组。
step 2. 明文串翻译:
对于每组字母对有三种情况
1: 两个字母在密钥表中位于同一行:”同行代换“,每个字母用其同行的下一位(如果没有下一位则用首位)代替。
2:两个字母在密钥表中位于同一列:”同列代换“,每个字母用其同列的下一位(如果没有下一位则用首位)代替。
3:不同行且不同列: 第一字母定行,第二字母定列,对应位置字母为密文的第一字母;第二字母定行,第一字母定列,对应位置字母为密文的第二字母。
即 明文= (key [a][b],key[c][d]),
则 密文= (key [a][d],key[c][b])。
按上述规则,将每组字母代换后,得到密文。
解密: 如果得到密钥单词,即可绘制密钥表,从而对应解密。
优点:单频次方法攻击无效
缺点:双频率法可攻破。
(虽然我也不知道这俩啥意思)
(后注:大概是说,在大样本前提下,依据概率论与数理统计知识,单个字母在英文中的使用频率基本固定,因此可以根据单个字母的出现频率依次对照,实现密码破译。双频率,即不看单个字母的频率,而看 “字母对“ 出现的频率。)
六、 置换密码:
通过置换矩阵加密信息。
加密方式:
part 1 绘制 置换矩阵
给定密钥单词,将密钥单词作为矩阵的第一行,
将明文串 从矩阵的第二行开始按序抄写,自动换行。
以此法得到置换矩阵
part 2 使用 置换矩阵
将 密钥单词更改顺序,对应列顺序一同更改(换列),从而得到密文
例:
密钥单词: hand
明文: meet at school
密钥表:
h a n d
m e e t
a t s c
h o o l
置换矩阵:
a d h n
e t m e
t c a s
o l h o
得密文: etmetcasolho
七、 一次一密 密码体制
即 基于以上各类古典密码,采取每次使用一个密钥,使用后即销毁密钥并更改密钥的方式。
优点: 随机性强、难以破解。
缺点: 制作密钥表工作量大;每次都需要进行密钥表的物理传递过程,中途可能被截获的概率极高。
八、 古典密码学展现的密码学思想
注:古典密码学中体现了现代密码学的核心思想——“扩散” 和 “混淆”
扩散: 即 将各个字母分布位置 在文章中打散,变得更加均匀。 一般依靠 “置换” 实现。
混淆: 即 调整各个字母在文章中出现的 频次,以打破相应统计学规律(防止频次攻击)。一般依靠 “代换” 实现。
第三讲 机械密码
- 两次世界大战中密码谍报对于战局的影响至关重要。 欧洲战局Enigma密码机、sigaba密码机,日本二战的 “紫色密码机”
- 所谓机械密码,即:基于古典密码理论,战争时期中 物理密码锁的实现
第四讲 现代密码学(※)
一、 现代密码学——知识大纲
密码学分为两大部分:密码编码学(即加密)密码分析学(即破译)
基础知识 :数论、物理学。(单向函数、陷门单向函数、杂凑函数等)
单钥密码 :DES、AES。 分组密码、流密码、消息认证码
双钥密码 :RSA、ECC。 公钥加密、数字签名
二、 对称密码体制(单钥密码)(传统密码)
1. 定义:
信息收发双方拥有相同的密钥
2. 单钥密码种类:
流密码: 将明文以 bit 或 字符 为单位, 分别与 密钥流 进行 加和取模运算, 得到密文。在二进制的情况下,则 %2,即异或运算。
分组密码: 先将明文划分为若干组,一般分组长度是 64bit 的倍数, 然后分组加密。 (因为计算机 2^64 位,计算得快)
3. DES单钥加密算法:Data Encryption Standard
分组与密钥长度: 将明文 以 64 bit / 组 进行分组; 密钥固定为 64 bit
算法流程:
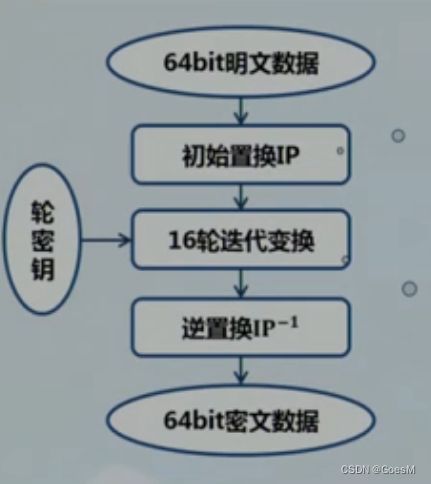
意义解析: 置换操作 以实现 扩散的目的; 迭代变换以 实现 混淆的目的; 多轮迭代变换 以增加数学组合,增加密码强度。
4. AES单钥加密算法: Advanced Encryption Standard
分组与密钥长度: 将明文 以 128 bit / 组 进行分组; 密钥长度根据安全性需求进行选择,一般为 128bit 192bit 256bit
算法流程:

意义解析:
从密码强度上来看,将 加和取模、代换、置换 三种古典密码方法综合使用,外加多轮迭代,加密性更强。
从使用实际上来看,根据安全性需求进行密钥长度的选择,提高了加密效率。
5. 详解链接: 单钥密码体制
三、非对称密码体制(双钥密码)(公钥密码)
1. 定义:
发送方和接收方使用不同的密钥,但这两个密钥都为一方拥有。
如果 A 要传送密文给 B,则使用B的公钥进行加密,B接收后用自己的私钥进行解密。
2. 密钥构造原理
用于构造公钥密码体制的函数依赖于各类数学难题。
其本质原理在于 用于加密的函数 为 单向函数 (难以逆解) 陷门单向函数 (知道陷门后则容易求逆,否则难以求逆)
3. Diffie 和 Hellman 提出公钥算法
数学基础:有限域上求离散对数。
4. RSA 算法
数学基础: 基于 大整数分解 为质因数的复杂性
优点: 极难破译
缺点: 加密也很慢
5. ECC 椭圆曲线 密码体制
数学基础: 基于 有限域上的 椭圆曲线点集 所构成的群上定义的离散对数
优点: 在相同安全性前提下,ECC的密钥更短。
6. 详解链接: 双钥密码体制
四、小结:
1. 单钥 与 双钥 对比
2. 三种算法的比较(DES与AES,RSA,ECC)
DES 密钥长度 固定为56位,当前已经可以被暴力打破
AES 密钥长度 可根据需求增长
RSA与ECC密钥长度即对应安全性如图:
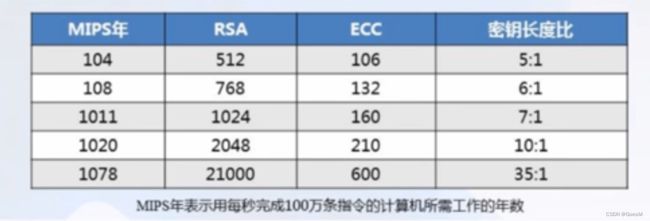
第五讲 密码破译
一、密钥破译方法
1. 直接窃取
就是直接偷,或者偷听
2. 密钥穷搜索
通过暴力搜索、字典攻击两种搜索方式,暴力搜索密钥
3. 密码分析攻击
根据数学理论进行密钥的分析。
四种分析方法:唯密文攻击、已知明文攻击、选择明文攻击、选择密文攻击。
4. 现代密码分析
- 确定性分析:通过已知量与已知的数学关系,进行密钥破译
- 统计性分析:利用明文的已知规律进行 破译
- 差分密码分析:通过明文的差值对于密文的影响,从而分析密钥
- 线性分析:对于单向函数求 线性近似表达式,从而分析
- 插值分析:根据拉格朗日差值法的思想,对加密算法(函数)进行等价变换。
- 密钥相关攻击:通过分析两个密钥之间的关系。
第六讲 密码的未来
- 量子计算机对密码的破译:量子计算机计算速度巨快,对于RSA公钥算法,因为其所应用的大整数分解数学理论在普通计算机中难以解决,但量子计算机可在分钟内解决。
- 量子密码: 通过量子形式作密码加密,具有不可窃听性。 量子性质:观测者的改变会改变信息的内容,因此当有人窃听密文时,窃听者和接收者所接受的量子信息也会发生改变,从而失去正确信息。
