java自制计算机_Java 应用:自制高精度计算器(2)
上一篇 文章讲了如何通过正则来将输入的表达式解析为多个 Token,而这篇文章的核心在于如何对 表达式求值。
我们输入的表达式,即我们通常见到的表达式,都是中缀表达式 —— 中缀的含义是,在表达式中,运算符是放中间的,比如 (1 + 2) * 3,运算符都是在数的中间。然而在计算机的世界里,还存在着前缀表达式和后缀表达式 —— 由名字也很容易知道,前缀表达式是将运算符放在数之前,后缀表达式是将运算符放到数之后。
表达式
形式
中缀
1 + (3 - 2) * 4 / 5
前缀
+ 1 / * - 3 2 4 5
后缀
1 3 2 - 4 * 5 / +
中缀表达式的劣势在于,一旦表达式复杂化,比如多层括号嵌套同时还要注意运算符的优先级,那么要编写计算中缀表达式的值的代码也十分的复杂。而对于前缀表达式和后缀表达式的计算,则十分的简单。
以后缀表达式为例:
从左往右扫描表达式,如果遇到数,那么将数入栈
如果遇到运算符,那么从栈中依次弹出两个数 n1 和 n2,使用该运算符对这两个数进行运算(n2 op n1),将获得的结果数入栈
重复 1 和 2 直到表达式扫描结束,那么栈中最后剩余的数便是表达式的值。
比如上面的例子,1 + (3 - 2) * 4 / 5 = 1.8,对于后缀表达式 1 3 2 - 4 * 5 / +:
当前 Token
操作
栈(栈顶在左边)
1
遇到数直接入栈
1
2
遇到数直接入栈
3 1
3
遇到数直接入栈
2 3 1
-
n1 = 2, n2 = 3;n2 op n1 = 3 – 2 = 1,并将 1 入栈
1 1
4
遇到数直接入栈
4 1 1
*
n1 = 4, n2 = 1;n2 op n1 = 4 * 1 = 4,并将 4 入栈
4 1
5
遇到数直接入栈
5 4 1
/
n1 = 5, n2 = 4;n2 op n1 = 4 / 5 = 0.8,并将 0.8 入栈
0.8 1
+
n1 = 0.8, n2 = 1;n2 op n1 = 1 + 0.8 = 1.8,并将 1.8 入栈
1.8
所以可见计算后缀表达式非常容易编码。
由 上一篇 文章可知,我们目前的 Expression 类所表示的,就是中缀表达式,所以我们需要提供算法,将中缀表达式转换为前缀表达式或者后缀表达式,从而方便我们计算表达式的值。当然,算法的流程,我们的计算机先辈们早就想出来了,而我们只需要做出实现即可。
同样以后缀表达式为例,中缀表达式转换为后缀表达式的算法流程如下:
初始化运算符栈 S 和用来保存中间结果的列表 L
从左往右扫描中缀表达式:
遇到数时,直接将其加入到 L
遇到运算符 op 时
2.1 如果 S 为空,那么直接将 op 入栈 S
2.2 如果 S 不空,并且 S 栈顶为左括号 '(',那么将 op 入栈 S
2.3 如果 S 不空,此时 S 栈顶为运算符,如果 op 的优先级大于 S 栈顶元素的优先级,那么将该运算符入栈 S
2.4 否则(即 op 的优先级小于 S 栈顶元素的优先级),将 S 的栈顶元素弹出,并将该元素加入 L;然后转到 2.1 继续判断并比较。
遇到括号时
3.1 如果是左括号 '(',直接将该左括号入栈 S
3.2 如果是右括号 ')',依次弹出 S 中的运算符,直到遇到一个左括号为止,然后将这一对括号都丢弃
将 S 中的剩余运算符依次弹出并加入 L
此时 L 中的所有的 Token 按顺序即为后缀表达式
(关于中缀、前缀、后缀表达式转换算法更详细的内容和例子,可以参考 前缀、中缀、后缀表达式 这篇文章,本文所写的算法流程也是参考这篇文章而来。)
根据上面的算法,我们就不难在目前的 Expression 基础上,写出将中缀表达式转换为后缀表达式的算法,我们将这个方法命名为 toPostfixExpr():
/**
* 获得该表达式的后缀形式
*
* @return 后缀表达式
*/
public Expression toPostfixExpr() {
ArrayDeque S = new ArrayDeque<>(); // 运算符栈
ArrayList L = new ArrayList<>(); // 保存中间结果的列表
for (Token token : tokens) {
switch (token.getType()) {
case NUMBER:
L.add(token);
break;
case OPERATOR:
Operator op = (Operator) token;
boolean back = true;
while (back) {
back = false;
if (S.isEmpty()) { // 运算符栈为空
S.push(op);
} else { // 运算符栈不为空
Token top = S.peek();
// 运算符栈栈顶为 '('
if (top.isBracket() && ((Bracket) top).isLeft()) {
S.push(op);
// op 的优先级大于运算符栈栈顶元素的优先级
} else if (op.isHigherThan((Operator) top)) {
S.push(token);
} else { // op 的优先级小于运算符栈栈顶元素的优先级
L.add(S.pop());
back = true; // 回到 while
}
}
}
break;
case BRACKET:
if (((Bracket) token).isLeft()) {
S.push(token);
} else {
for (Token t = S.pop();
!t.isBracket(); t = S.pop()) {
L.add(t);
}
}
break;
}
}
while (!S.isEmpty()) {
L.add(S.pop());
}
return new Expression(L, true); // true 表示该表达式为后缀表达式
}
此时我们往 Expression 中添加了一个 boolean 字段 postfix,用来标识该表达式是否为后缀表达式,postfix 默认为 false,如果为 true 则表明该表达式是后缀表达式。
public class Expression {
...
private final List tokens; // 该表达式中的所有 Token
private final boolean postfix; // 该表达式是否为后缀表达式的标识
public Expression(List tokens, boolean postfix) {
this.tokens = tokens;
this.postfix = postfix;
}
/**
* 该表达式是否为后缀表达式
*
* @return 如果该表达式为后缀表达式返回 true,否则返回 false
*/
public boolean isPostfix() {
return postfix;
}
...
}
然后,根据后缀表达式,我们也很容易写出计算表达式值的方法,我们将方法命名为 calculate():
/**
* 通过后缀表达式计算表达式的值
*
* @return 表达式的值
*/
public Num calculate() {
if (!isPostfix()) {
throw new RuntimeException("请先将表达式转为后缀表达式再计算");
}
ArrayDeque stack = new ArrayDeque<>();
for (Token token : tokens) {
if (token.isNumber()) {
stack.push(token);
} else {
Num n1 = (Num) stack.pop();
Num n2 = (Num) stack.pop();
Operator op = (Operator) token;
Num result = n2.operate(op, n1);
stack.push(result);
}
}
if (stack.size() != 1) { // 栈中最后剩下的不止一个数,说明表达式有问题
throw new RuntimeException("错误的表达式");
}
return (Num) stack.pop();
}
此时我们在 Num 类中定义了一个 operate 方法,用来根据运算符对两个数进行运算:
public static final RoundingMode MODE
= RoundingMode.HALF_UP; // 默认对末尾小数采用 四舍五入
public static final MathContext MATH_CONTEXT
= new MathContext(6, MODE); // 无限循环时保留6位有效数字,末位四舍五入
public Num operate(Operator op, Num other) {
BigDecimal result = null;
switch (op.value()) {
case '+':
result = value.add(other.value);
break;
case '-':
result = value.subtract(other.value);
break;
case '*':
result = value.multiply(other.value);
break;
case '/':
result = value.divide(other.value, MATH_CONTEXT);
break;
}
if (result == null) {
throw new RuntimeException(String.format(
"operate 方法出错:%s %s %s", value, op.text(), other.value));
}
return new Num(result);
}
目前来看一切都很完美 —— 但是我们忽略了一种情况,那就是输入负数的情况。而此时存在以下两种情况:
输入的表达式开头是负数,比如 -1 + 2 * 3,这种情况容易解决,我们只需要在开头补上一个 0,便能适应现在的程序,比如该表达式补上 0 后就成为 0 - 1 + 2 * 3,结果一致
另一种情况就是表达式中出现负数了 —— 此时我们需要对负数进行特殊的标识,比如按照一般情况将负数使用括号()包围。所以我们需要补充我们的正则表达式,让其可以匹配类似于 (-12) 和 (-100.100) 这样的 Token。
修改之后的 Expression(\(-(\d*\.\d+|\d+)\) 用来匹配负数):
public class Expression {
private static final String REG_EXPR = "\\s*((\\(-(\\d*\\.\\d+|\\d+)\\))|(\\d*\\.\\d+|\\d+)|(\\+|-|\\*|/)|(\\(|\\))|([A-Za-z]+\\(.*\\)))\\s*";
private static final Pattern PATTERN = Pattern.compile(REG_EXPR);
...
private static Token getToken(Matcher matcher) {
// matcher.group(0) 匹配整个正则,matcher.group(1) 匹配第一个括号
String m = matcher.group(1);
if (m != null) {
if (matcher.group(2) != null) { // 负数
// matcher.group(3) 提取形如 (-1.2) 中的 1.2
return new Num("-" + matcher.group(3));
} else if (matcher.group(4) != null) { // 正数
return new Num(matcher.group(4));
} else if (matcher.group(5) != null) { // 运算符
return new Operator(matcher.group(5).charAt(0));
} else if (matcher.group(6) != null) { // 括号
return new Bracket(matcher.group(6).charAt(0));
} else if (matcher.group(7) != null) { // 函数
Function function = new Function(matcher.group(7));
Num num = function.getResult(); // 直接计算出函数的值作为 Token
return num;
}
}
throw new RuntimeException("getToken"); // 正则无误的情况下不会发生
}
...
}
现在,让我们来写一个主类,从命令行获得输入并且计算输入的表达式的值。我们将主类命名为 Launcher:
public class Launcher {
public static void main(String[] args) throws Exception {
System.out.println("欢迎使用你的计算器(输入 e(xit) 退出)");
try (Reader in = new InputStreamReader(System.in);
BufferedReader reader = new BufferedReader(in)) {
String line;
while (true) {
System.out.print("> ");
line = reader.readLine();
if (null == line
|| "e".equalsIgnoreCase(line)
|| "exit".equalsIgnoreCase(line)) {
break;
} else if (line.isEmpty()) {
continue;
}
try {
Expression expr = Expression.of(line);
Expression postfixExpr = expr.toPostfixExpr();
Num result = postfixExpr.calculate();
System.out.println(result);
} catch (ArithmeticException ex) {
System.out.println("运算错误:" + ex.getMessage());
} catch (RuntimeException ex) {
System.out.println("运行错误:" + ex.getMessage());
// ex.printStackTrace(System.err);
}
}
}
}
}
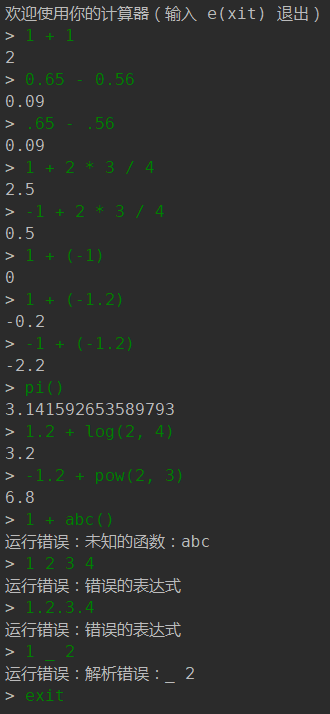
可以看到,我们已经可以成功的解析表达式,并且计算表达式的值(完整的源码在 GitHub)。
当然,我们总不能每次运行都用 Maven 来运行项目,所以我们把项目打包成 jar,然后写个脚本来执行这个 jar,最后将脚本加入到 PATH 中,那么便可以在命令行下直接调用。
我们将打包的 jar 命名为 mcalc.jar (打包的配置可参考 pom.xml),然后写个简单的脚本。比如,在 Windows 上,写个 mcalc.bat:
@echo off
:: %~dp0 表示当前批处理文件所在目录的路径
set DIR_PATH=%~dp0
java -jar %DIR_PATH%mcalc.jar
然后将 mcalc.bat 和 mcalc.jar 放到同一个文件夹下,然后将这个文件夹的路径加入到 PATH。此时在命令行中直接输入 mcalc,便可以进入程序:
参考: