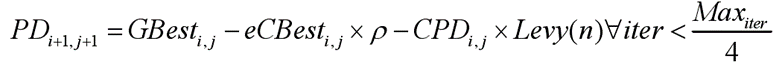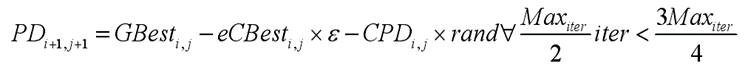智能优化算法之土拨鼠优化算法（PDO），原理公式详解，附matlab代码

土拨鼠优化算法（Prairie Dog Optimization Algorithm，PDO）是一种新兴的智能优化算法。该成果于2022年发表在知名SCI，CCF推荐期刊Neural Computing and Applications。目前谷歌学术上查询被引177次。

PDO的基本思想是将土拨鼠的行为分为两个阶段。第一阶段为全局探索阶段，分为两种行为模式：食物搜索行为和构筑洞穴行为；第二阶段为局部开发阶段，分为两种行为模式：对食物源信号和捕食者信号的反应行为。

算法原理

（1）探索阶段

探索阶段有两种策略：

策略一：由个体在巢穴内寻找新的食物来源，数学模型如下式表示：

策略二：个体会不断挖掘新的洞穴，数学模型如下式表示：

其中PDi,j为个体所处位置。GBesti,j为当前全局最优解，Levy(n)为标准列维飞行，ρ为本实验固定在0.1Hz的专门食物源报警器。eCBesti,j、CPDi,j和DS的数学模型公式如下：

eCBesti,j评估当前获得的最优解的效果，△表示一个极小的数，表明草原犬的个体之间存在差距。

CPDi,j为群体中所有草原犬的随机累计效应，rPD为随机解的位置：

DS为小团体的挖掘强度，它取决于食物源的质量，r引入随机性质以确保探索的性能，当迭代次数为奇数时为-1，为偶数时为1。Maxiter为最大迭代次数，iter为当前迭代次数。

（2）开发阶段

在开发阶段，第一种声音可以传递食物的来源与食物源的质量，当有个体发现了高质量的食物来源，其余个体会聚集在声源位置以满足它们的食物需求，该情况的位置更新数学模型如下式表示：

第二种声音为警示同类捕食者的存在，捕食者行进路线上的同类会躲藏起来，该情况的位置更新数学模型如下式表示：

其中PE表示捕食者效应，rand为[0,1]中的随机数。

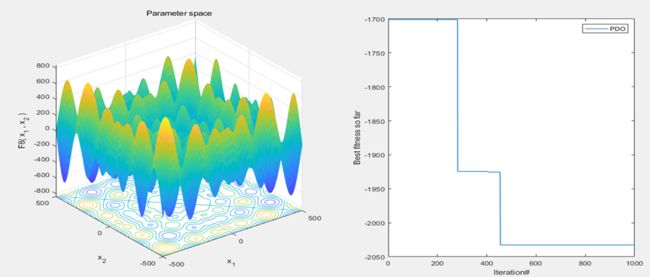
结果展示

以为CEC2005函数集为例，进行结果展示：

 MATLAB核心代码

% 土拨鼠优化算法（PDO）
function [Best_PD,PDBest_P,PDConv]=PDO1(N,T,LB,UB,Dim,F_obj)
PDBest_P=zeros(1,Dim);           % best positions
Best_PD=inf;                    % global best fitness
X=initializationPDO(N,Dim,UB,LB); %Initialize the positions of solution
Xnew=zeros(N,Dim);
PDConv=zeros(1,T);               % Convergance array
M=Dim;                      %set number of coteries 


t=1;                         % starting iteration
rho=0.005;                   % account for individual PD difference
% eps                         %food source quality 
epsPD=0.1;                  % food source alarm
OBest=zeros(1,size(X,1));     % old fitness values
CBest=zeros(1,size(X,1));     % new fitness values


for i=1:size(X,1) 
Flag_UB=X(i,:)>UB; % check if they exceed (up) the boundaries
Flag_LB=X(i,:)=T/4)
                    Xnew(i,j)=PDBest_P(1,j)*X(randi([1 N]),j)*DS*RL(i,j);
                elseif (t<3*T/4 && t>=2*T/4)
                    Xnew(i,j)=PDBest_P(1,j)*PE*rand;
                else
                    Xnew(i,j)=PDBest_P(1,j)-eCB*eps-cpd*rand;
                end
        end


            Flag_UB=Xnew(i,:)>UB; % check if they exceed (up) the boundaries
            Flag_LB=Xnew(i,:)

参考文献

[1] Absalom E. Ezugwu, Jeffrey O. Agushaka, Laith Abualigah, Seyedali Mirjalili, Amir H Gandomi, “Prairie Dog Optimization Algorithm” Neural Computing and Applications, 2022. DOI: 10.1007/s00521-022-07530-9.

[2] 袁磊. 基于知识共享优化算法和草原犬优化算法分析及应用研究[D]. 广西民族大学，2023

完整代码获取方式：后台回复关键字：TGDM827