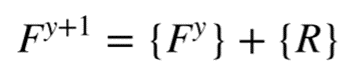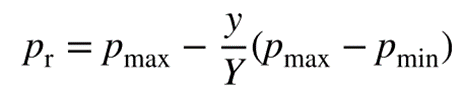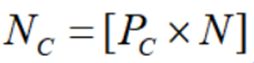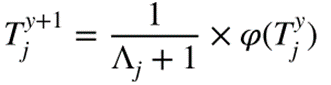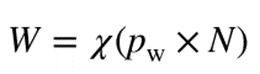智能优化算法之季节优化算法（SOA），原理公式详解，附matlab代码

季节优化算法（Seasons optimization algorithm，SOA）是一种新的随机仿生优化算法，该算法的灵感来自于树木在一年中不同季节的生长周期。该成果于2020年发表在知名SCI期刊Engineering with Computers上。目前谷歌学术上查询被引13次。

SOA算法通过更新、竞争、播种和移除四个主要操作对森林中的树木进行更新，最后选取最强树作为最优解。

算法原理

（1）树木更新阶段

算法首先创建一个随机分布的森林F，定义为F=[T1,T2,...,Tn]，更新算子用于模拟树木在春季的行为，该更新算子的数学模型如下式表示：

其中Fy为第y次迭代时的森林，R为新生成的幼苗集合，如下所示:

其中Pr表示更新速率，Ay表示去年秋天落在土地上的种子数。函数Φ在森林的不同区域随机生成Pr×Ay新幼苗。Φ模拟了几种种子的自然发芽并长成幼苗的过程。在自然界中，只有少数种子有机会成长为一棵树，Pr的数学模型如下式表示：

其中Y为最大迭代次数，y为当前迭代次数。经实证检验，Pmin和Pmax分别设为0.4和0.6。

（2）树木竞争阶段

竞争阶段模拟了夏季对树木生长的影响。首先，树木按照其强度递减的顺序进行排序。然后选择最强树的Nc，形成核心树列表Γ=[T1, T2，…，TNc]。Nc的数学模型如下式表示：

其中PC是一个随机数，它识别出要作为核心树的树的分数，然后从相邻树中随机选取Zi树，形成核心树Ti∈Γ的邻域区。在每个邻域i内，为了数学模拟竞争对一棵树Tj的影响，提出如下方程:

其中Tjy为树Tj在迭代y中的位置。Λj为度量拥挤度或竞争指数，计算相邻树对树Tj的影响。

（3）树木播种阶段

为了模拟树木在秋季播种过程的行为，首先随机选取几棵树形成播种列表Υ={T1, T2，…，TA}。这些树就有机会在森林里传播它们的种子。种子数(A)的数学模型如下式表示：

其中Ps为随机数，表示播种速率。函数  从森林中选择Ps×N最强的树。

（4）树木移除阶段

为模拟冬季对树木的影响，该操作符从森林中移除弱树。强度最小的树被认为是弱树，移除工作对森林的影响模型如下:

其中W是将从森林中移除的弱树集合，W的数学模型如下式表示：

其中函数x(.)从森林中去除Pw×N棵树，Pw为抗性率，其数学模型如下式表示:

其中x为负值，表示树木可能受损和倒塌的临界温度。实际上，x的取值范围为[−100,0)，但为了保持一致性，它的值被映射为[−1,0)。

结果展示

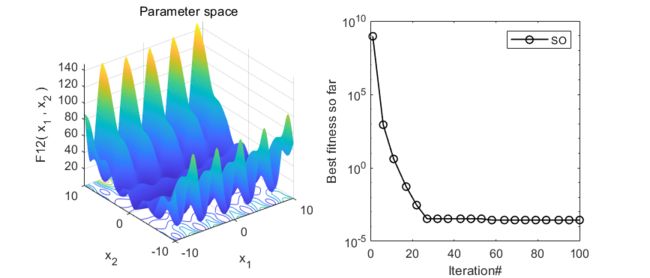
以为CEC2005函数集为例，进行结果展示：

 MATLAB核心代码

% 季节优化算法（POA）
clear all;
clc;


%% Problem Statement
func_name = 'F12';
ProblemParams.CostFuncName = func_name;
[lowerbound, upperbound, dimension,fobj]=fun_info(ProblemParams.CostFuncName);
ProblemParams.CostFuncName=fobj;
ProblemParams.lb=lowerbound;
ProblemParams.ub=upperbound;
ProblemParams.NPar = dimension;




ProblemParams.VarMin =ProblemParams.lb;
ProblemParams.VarMax = ProblemParams.ub;


if numel(ProblemParams.VarMin)==1
    ProblemParams.VarMin=repmat(ProblemParams.VarMin,1,ProblemParams.NPar);
    ProblemParams.VarMax=repmat(ProblemParams.VarMax,1,ProblemParams.NPar);
end
ProblemParams.SearchSpaceSize = ProblemParams.VarMax - ProblemParams.VarMin;
AlgorithmParams.NumOfTrees = 8;
AlgorithmParams.NumOfYears = 100;
AlgorithmParams.Pmin = 0.1;
AlgorithmParams.Pmax = 0.8;




%% Main Loop


for year= 1:AlgorithmParams.NumOfYears
    p=AlgorithmParams.Pmax-(year/AlgorithmParams.NumOfYears)*(AlgorithmParams.Pmax-AlgorithmParams.Pmin);            %pr, ps and pw are in the range [0.4, 0.6]
    AlgorithmParams.RenewRate=p;
    AlgorithmParams.SeedingRate=p;
    AlgorithmParams.ColdThreshold=p;
    AlgorithmParams.CompetitionRate = p;
    %% Spring Season
    if (year==1)
        InitialTrees = CreateForest(AlgorithmParams, ProblemParams);
        Forest=InitialTrees;
        InitialCost = feval(ProblemParams.CostFuncName,InitialTrees');
        Forest(:,end+1) = InitialCost';
    else
        Forest = Renew(Forest, Seeds, AlgorithmParams, ProblemParams);
    end
    
    
    %% Summer Season  (Growth & Competition)
    [Forest] = Competition (Forest, AlgorithmParams, ProblemParams, year);
    %% Autumn Season
    Seeds = Seeding(Forest,AlgorithmParams, ProblemParams);
    s=size(Seeds,1);
    AlgorithmParams.s=s;
    %% Winter Season
    Forest = Resistance(Forest,AlgorithmParams, ProblemParams);
    Costs = Forest(:,end);
    MinimumCost(year) = min(Costs);
    fprintf('Minimum Cost in Iteration %d is %3.16f \n', year,MinimumCost(year));
end

参考文献

[1] Emami H. Seasons optimization algorithm[J]. Engineering with Computers, 2022, 38(2): 1845-1865.

完整代码获取方式：后台回复关键字：TGDM827