AcWing第三章算法模板总结——搜索与图论
一、DFS与BFS
二、树与图的遍历:拓扑排序
三、最短路径
四、最小生成树
五、二分图:染色法、匈牙利算法
一、DFS与BFS
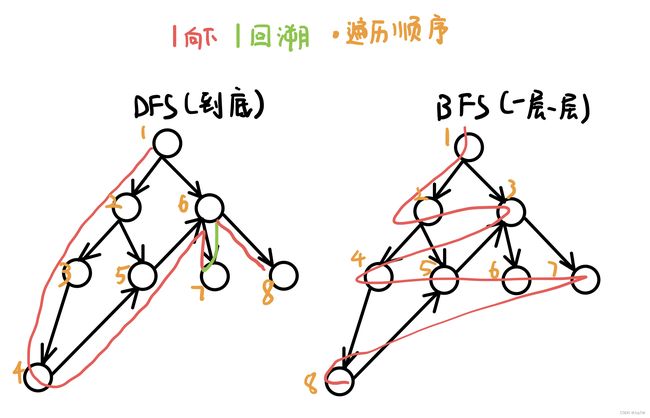
(一)DFS(深度优先遍历)
1、使用栈(stack)实现。
2、DFS所需要的空间是树的高度h
3、搜索到某个节点不具有最短性
4、回溯:回溯的时候,一定要记得恢复现场
5、剪枝:提前判断某个分支一定不合法,直接剪掉该分支
例题:
842.排列数字
题目描述
给定一个整数n,将数字1~n排成—排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1 ≦ n ≦ 7
输入样式:
3
输出样式:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
#include例题:
843.n-皇后问题
题目描述
n-皇后问题是指将n个皇后放在n*n的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
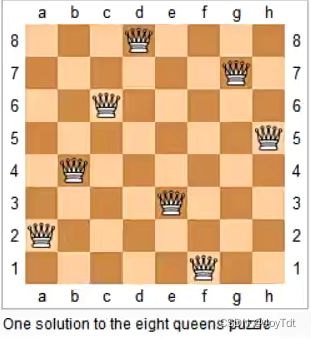
现在给定整数n,请你输出所有的满足条件的棋子摆法。
输入格式
共—行,包含整数n。
输出格式
每个解决方案占n行,每行输出一个长度为n的字符串,用来表示完整的棋盘状态。其中"."表示某一个位置的方格状态为空,"Q"表示某一个位置的方格上摆着皇后。每个方案输出完成后,输出一个空行。
数据范围
1 ≦ n ≦ 9
输入样式:
4
输出样式:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
分析:
只要满足这一行,这一列,主对角线,和副对角线上没有被使用,就可以落子

代码:
#include(二)BFS(广度优先遍历)
1、使用队列(queue)实现。
2、BFS需要的空间是2h
3、搜索到某个节点一般是具有最短性的路径,通常来说,求“最短”的操作,都可以用BFS来做
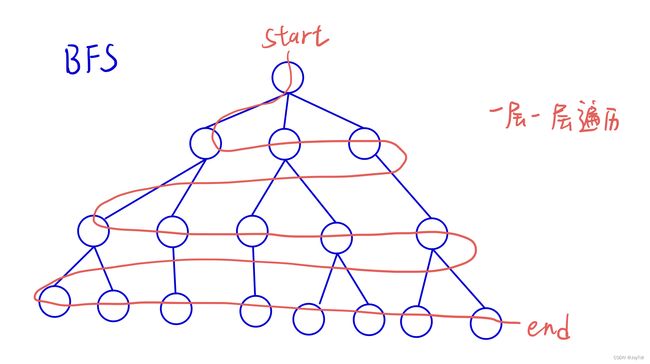
基本框架:

844.走迷宫
题目描述
给定一个n*m的二维整数数组,用来表示一个迷宫,数组中只包含0或1,其中0表示可以走的路,1表示不可通过的墙壁。
最初,有一个人位于左上角(1,1)处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。请问,该人从左上角移动至右下角(n, m)处,至少需要移动多少次。
数据保证(1,1)处和(n, m)处的数字为0,且一定至少存在一条通路。
输入格式
第—行包含两个整数n和m。
接下来n行,每行包含m个整数((O或1),表示完整的二维数组迷宫。
输出格式
输出路径。
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1 ≦ m ≦ n ≦ 100
输入样式:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样式:
4 4
3 4
2 4
2 3
2 2
2 1
2 0
1 0
8
代码:
#include二、树与图的遍历:拓扑排序
树是特殊的图,无环连通图。
图分为两种:有向图和无向图
(一)树与图的存储

1、邻接矩阵:g[a][b] 存储边a->b
2、邻接表(n是节点数,e是边数)
模板代码:
const int N = 100010, M = N * 2;
// h[k]存储这个单链表的头结点。e存储节点的值。ne存的是每个节点的next值
int h[N], e[M], ne[M], idx;
// 添加一条边a->b
void add(int a, int b) // 头插至h[a]后面
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// 初始化
idx = 0;
memset(h, -1, sizeof h);
(二)树和图的遍历
1、深度优先遍历(递归)
const int N = 100010, M = N * 2;
// h[k]存储这个单链表的头结点。e存储节点的值。ne存的是每个节点的next值
int h[N], e[M], ne[M], idx;
bool st[N]; // 存储某个值是否遍历过
int dfs(int u)
{
st[u] = true; // 表示点u已经被遍历过
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j]) dfs(j);
}
}
例题:
846.树的重心
题目描述
给定一颗树,树中包含n个结点(编号1~n)和n-1条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。

输入格式
第一行包含整数n,表示树的结点数。
接下来n-1行,每行包含两个整数a和b,表示点a和点b之前存在一条边。
输出格式
输出一个整数m,表示重心的所有的子树中最大的子树的结点数目。
数据范围
1 ≦ n ≦ 10^5
输入样式:
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样式:
4
代码:
#include模板:
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true; // 表示点j已经被遍历过
q.push(j);
}
}
}
例题:
847.图中点的层次
题目描述
给定一个n个点m条边的有向图,图中可能存在重边和自环。
请你求出1号点到n号点的最短距离,如果从1号点无法走到n号点,输出-1。
请你求出1号点到n号点的最短距离,如果从1号点无法走到n号点,输出-1。
输入格式
第一行包含两个整数n和m。
接下来m行,每行包含两个整数a和b,表示存在一条从a走到b的长度为1的边。
输出格式
输出一个整数,表示1号点到n号点的最短距离。
数据范围
1 ≦ n ,m ≦ 10^5
输入样式:
4 5
1 2
2 3
3 4
1 3
1 4
输出样式:
1
题目代码:
#include3、时间复杂度
| 邻接矩阵 | 邻接表 | |
|---|---|---|
| DFS | O(n²) | O(n+e) |
| BFS | O(n²) | O(n+e) |
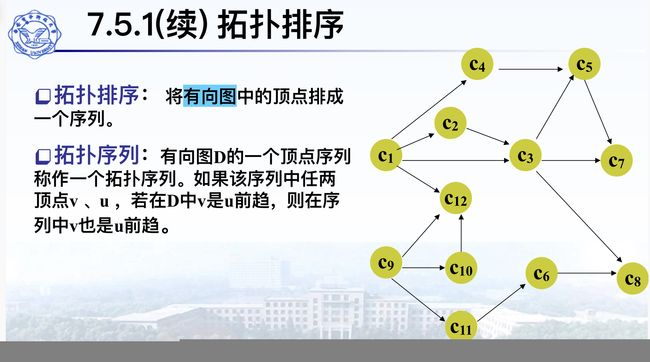
4、BFS的应用:拓扑序列
什么是拓扑序:将一个有向图的很多节点,排成一个序列,使得图中的所有边,都是从前面的节点,指向后面的节点。则这样一个节点的排序,称为一个拓扑序。
可以证明,一个有向无环图,一定存在一个拓扑序列。有向无环图,又被称为拓扑图。
对于每个节点,存在2个属性,入度和出度。
入度,即,有多少条边指向自己这个节点。
出度,即,有多少条边从自己这个节点指出去。
所有入度为0的点,可以排在当前最前面的位置。

848.有向图的拓扑序列
题目描述
给定一个n个点m条边的有向图,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出-1。
若一个由图中所有点构成的序列A满足:对于图中的每条边(x, y),x在A中都出现在y之前,则称A是该图的一个拓扑序列。
输入格式
第一行包含两个整数n和m。
接下来m行,每行包含两个整数x和y,表示点x和点y之间存在一条有向边(x, y)。
输出格式
共—行,如果存在拓扑序列,则输出拓扑序列。
否则输出-1。
数据范围
1 ≦ n ,m ≦ 10^5
输入样式:
3 3
1 2
2 3
1 3
输出样式:
1 2 3
#include三、最短路径
最短路径和dp问题的关系:dp问题可以看成最短路径的特殊情况。
在最短路问题中,源点也就是起点,汇点也就是终点。
(一)简述
一、单源最短路:指的是求一个点,到其他所有点的最短距离。(起点是固定的,单一的)
根据是否存在权重为负数的边,又分为两种情况:
第一种为所有边都是正数,共有两种:
- 朴素Dijkstra:时间复杂度O(n2),其中n是图中点的个数,m是边的个数。
- 堆优化版的Dijkstra:时间复杂度O(mlogn)
两者孰优孰劣,取决于图的疏密程度(取决于点数n,与边数m的大小关系)。当是稀疏图(n和m是同一级别)时,可能堆优化版的Dijkstra会好一些。当是稠密图时(m和n2是同一级别),使用朴素Dijkstra会好一些。
第二种为存在负权的边,共有两种:
- Bellman-Ford:时间复杂度O(nm)
- SPFA:时间复杂度一般是O(m),最差O(nm),是前者的优化版,但有的情况无法使用SPFA,只能使用前者,比如要求最短路不超过k条边,此时只能用Bellman-Ford
二、多源汇最短路:起点和终点都是不确定的,(起点不是固定的,而是多个)
Floyd算法:(时间复杂度O(n3))
三、算法的选用:通常来说,单源最短路的,如果没有负权重的边,用Dijkstra,有负权重边的,通常用SPFA,极少数用Bellman-Ford;多源汇最短路的,用Floyd。
Dijkstra基于贪心,Floyd基于动态规划,Bellman-Ford基于离散数学。
最短路问题的核心在于,把问题抽象成一个最短路问题,并建图。图论相关的问题,不侧重于算法原理,而侧重于对问题的抽象。
(二)具体算法
849.Dijkstra求最短路Ⅰ
题目描述
给定一个n个点m条边的有向图,图中可能存在重边和自环,所有边权均为正值。请你求出1号点到n号点的最短距离,如果无法从1号点走到n号点,则输出-1。
输入格式
第一行包含整数n和m。
接下来m行每行包含三个整数x,y,z,表示点x和点y之间存在一条有向边,边长为z。
输出格式
输出一个整数,表示1号点到n号点的最短距离。
如果路径不存在,则输出-1。
数据范围
1 < n ≤ 500,
1 ≤ m ≤ 10^5,
图中涉及边长均不超过10000。
输入样式:
3 3
1 2 2
2 3 1
1 3 4
输出样式:
3
1、朴素Dijkstra算法
时间复杂度为 O(n²+m), n 表示点数,m 表示边数
假设图中一共有n个点,下标为1~n。下面所说的某个点的距离,都是指该点到起点(1号点)的距离。
算法步骤如下,
①定义用到的数据
int n,m; // n个点,m条边
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
②初始化距离
使用dist数组表示距离,dist[1] = 0,dist[i] = +∞;即,将起点的距离初始化为0,而其余点的距离当前未确定,用正无穷表示。实际算法可以用比较大的数表示正无穷。
③for循环n次
从距离已知的点中,每次选取一个不在st集合中,且距离最短的点(这一步可以用小根堆来优化),遍历该点的所有出边,更新这些出边所连接的点的距离。并把该次选取的点加入到集合st中,因为该点的最短距离此时已经确定。
当所有点都都被加入到st中,表示全部点的最短距离都已经确定完毕
注意某个点的距离已知,并不代表此时这个点的距离就是最终的最短距离。在后续的循环中,可能用一条更短距离的路径,去更新。

代码:
#include2、堆优化版的Dijkstra算法
最重要的是具体用到的数据结构:
int n,m;
int h[N], w[N], e[N], ne[N], idx; // w代表权重,其他是图使用单链表实现
bool st[N]; // 存储每个点的最短路是否已经确定
priority_queue, greater> heap;
时间复杂度 O(mlogn), n 表示点数,m 表示边数
优化:相比于普通的Dijkstra算法,在寻找距离最短的点的时候,这里优化为使用小根堆来找最短距离的点。从而缩减执行时间!
可以自己手写堆(用数组模拟,int h[N], e[N], ne[N], idx;),也可以使用现成的(C++的STL提供了priority_queue )
特别注意,插入堆的操作,由于更新距离时,可能对一些距离已知的点进行更新(更新为更小的距离),此时不能因为这个点已经在堆中就不进行插入了,因为其距离已经变了,堆中原有的节点已经无效了,按理说,应该修改堆中对应节点的距离值,然后做调整,实际上,可以直接插入一个新的节点(此时对于同一个节点,堆中有两份),但没有关系,堆中的重复节点不会影响最终的结果。
也可以使用STL的模板,建造堆priority_queue
Type 就是数据类型,Container 就是容器类型(Container必须是用数组实现的容器,比如vector,deque等等,但不能用 list。STL里面默认用的是vector),Functional 就是比较的方式,当需要用自定义的数据类型时才需要传入这三个参数,使用基本数据类型时,只需要传入数据类型,默认是大顶堆。
#include 3、Bellman-Ford算法
最重要的是具体用到的数据结构:
int n, m; // n表示点数,m表示边数
int dist[N]; // dist[x]存储1到x的最短路距离
struct Edge // 边,a表示出点,b表示入点,w表示边的权重
{
int a, b, w;
}edges[M];
适用于所有负权边的情况。(n是点的个数)

可以使用C++里面的结构体来定义边,存储a,b,w。表示存在一条边a点指向b点,权重为w。则遍历所有边时,只需要遍历所有的结构体数组即可。
循环的次数的含义:假设循环了k次,则表示,从起点,经过不超过k条边,走到每个点的最短距离。
该算法能够保证,在循环n次后,对所有的边(a, b, w),都满足dist[b] <= dist[a] + w。这个不等式被称为三角不等式。这个更新操作(dist[b] = min(dist[b], dist[a] + w))称为松弛操作。
注意:
1、有负权回路,不一定存在最短路径

2、判断图中是否存在负权回路——可以用来找负环
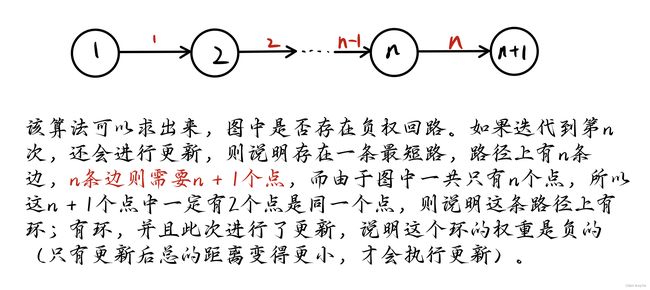
但求解负权回路,通常用SPFA算法,而不用Bellman-Ford算法,因为前者的时间复杂度更低。
由于循环了n次,每次遍历所有边(m条边)。故Bellman-Ford算法的时间复杂度是O(n×m),nn 表示点数,mm 表示边数
注意在模板题中需要对下面的模板稍作修改,加上备份数组,详情见模板题。
模板:
int n, m; // n表示点数,m表示边数
int dist[N]; // dist[x]存储1到x的最短路距离
struct Edge // 边,a表示出点,b表示入点,w表示边的权重
{
int a, b, w;
}edges[M];
// 求1到n的最短路距离,如果无法从1走到n,则返回-1。
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
// 如果第n次迭代仍然会松弛三角不等式,就说明存在一条长度是n+1的最短路径,由抽屉原理,路径中至少存在两个相同的点,说明图中存在负权回路。
for (int i = 0; i < n; i ++ ) // 遍历n次
{
for (int j = 0; j < m; j ++ ) // 每次判断m个边
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > dist[a] + w)
dist[b] = dist[a] + w;
}
}
if (dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];
}
只能用Bellman-Ford算法做的题:
853.有边数限制的最短路
4、SPFA算法 (做队列优化的Bellman-Ford算法)
若要使用SPFA算法,一定要求图中不能有负权回路。只要图中没有负权回路,都可以用SPFA,这个算法的限制是比较小的。
SPFA其实是对Bellman-Ford使用队列进行的一种优化。
它优化的是这一步:d[b] = min(d[b], d[a] + w)
我们观察可以发现,只有当d[a]变小了,才会在下一轮循环中更新d[b]
考虑用BFS来做优化。用一个队列queue,来存放距离变小的节点。
(和Dijkstra很像)
SPFA的好处:能解决无负权边的问题,也能解决有负权边的问题,并且效率还比较高。但是当需要求在走不超过k条边的最短路问题上,就只能用Bellman-Ford算法了。
时间复杂度 平均情况下 O(m),最坏情况下 O(nm), n 表示点数,m 表示边数
代码:
#includeSPFA还可以被用来判断图中是否存在负环
核心步骤:
1、首先开辟一个cnt[n]数组,用来记录从1号点到每个节点的最短路径中所经过的节点个数
2、要把所有节点放入队列
3、然后在每次更新dist数组的时候维护这个cnt数组。并且判断,如果当前cnt[j]的值大于n(节点个数),说明图中有负环
时间复杂度是 O(nm), n 表示点数,m 表示边数
int n; // 图中节点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N], cnt[N]; // dist[x]存储1号点到x的最短距离,cnt[x]存储1到x的最短路径中所经过的点数
bool st[N]; // 存储每个点是否在队列中
// 如果存在负环,则返回true,否则返回false。
bool spfa()
{
// 不需要初始化dist数组
// 原理:如果某条最短路径上有n个点(除了自己),那么加上自己之后一共有n+1个点,由抽屉原理一定有两个点相同,所以存在环。
// 主要cnt[x]只要大于等于 n了,则可以说明图中有负环
queue<int> q;
for (int i = 1; i <= n; i ++ ) // 要把所有节点放入队列
{
q.push(i);
st[i] = true;
}
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true; // 如果从1号点到x的最短路中包含至少n个点(不包括自己),则说明存在环
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
5、Floyd算法 (进行队列优化的Bellman-Ford算法)
适用情况:求解多源汇最短路问题,也能处理边权为负数的情况,但是无法处理存在负权回路的情况。
使用邻接矩阵来存储图。初始使用d[i][j]来存储这个图,存储所有的边
算法思路:
for(k = 1; k <= n; k++)
for(i = 1; i <= n; i++)
for(j = 1; j <= n; j++)
d[i,j] = min(d[i,j] , d[i,k] + d[k,j])
结束后,d[i][j]存的就是从点 i 到 j 的最短路的长度。
Floyd算法 的原理是基于动态规划(DP)(具体原理在后续的动态规划章节细说)。
其状态表示是:d(k, i, j),从 i 这个节点出发,只经过1 ~ k这些中间点,到达点j的最短距离
模板代码:
// 初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示 a到 b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
四、最小生成树
(一)简述
对应的都是无向图。
在给定一张无向图,如果在它的子图中,任意两个顶点都是互相连通,并且是一个树结构,那么这棵树叫做生成树。当连接顶点之间的图有权重时,权重之和最小的树结构为最小生成树!
常用算法如下图:

一般情况下,稀疏图使用克鲁斯卡尔算法,稠密图使用朴素版Prim算法。
Prim算法简单说其实就是找相邻最小边,然后把点加入集合
Kruskal算法简单来说其实就是找整个图中最小的边,然后把边加入集合
(二)具体算法
1、朴素版Prim算法(加点)
算法流程(核心):
memset(dit, 0x3f, sizeof dist);
for(int i = 0; i < n; i++)
{
t <- 找到不在集合s中, 且距离最近的点
用t来更新其他点到集合s的距离(Dijkstra算法是更新其他点到源点的距离)
将t加入到集合s中(st[]=true)
}
注意,一个点t到集合s的距离,指的是:若点t和集合s中的3个点有边相连。则点t到集合s的距离就是,t与3个点相连的边中,权重最小的那条边的权重。
时间复杂度是 O(n^2+m), n 表示点数,m 表示边数
模板代码:
int n; // n表示点数
int g[N][N]; // 邻接矩阵,存储所有边
int dist[N]; // 存储其他点到当前最小生成树这个集合的距离
bool st[N]; // 存储每个点是否已经在生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
memset(dist, 0x3f, sizeof dist); // 1、初始化dist为正无穷
int res = 0;
for (int i = 0; i < n; i ++ ) // 2、n次迭代,代表第i个加入的点
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j])) // 3、找到集合外(!st[j])距离集合最近的点
t = j;
if (i && dist[t] == INF) return INF; // 如果不是第一条边且(当前距离集合最近的点,距离集合的距离是正无穷),所以不存在最小生成树
if (i) res += dist[t];
st[t] = true;
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]); // 4、更新其他点到集合的距离
}
return res;
}
上面先累加res,再执行更新其他点到集合的距离。这两个操作的顺序不能出错。
例题:
Acwing-858.Prim算法求最小生成树
2、堆优化版Prim算法
基本不会用到,这里就偷个懒,不写了。
3、Kruskal(克鲁斯卡尔)算法(加边)
时间复杂度是 O(mlogm), n 表示点数,m 表示边数。
这里还使用到了并查集,判断a和b是否连通
算法思路:
1、先将所有边 按照权重 从小到大排序(可以用sort)
2、从小到大枚举每条边(a,b,w)——a->b权重是w
3、若a,b不连通(并查集中的祖宗节点是否一致),则将这条边,加入集合中(将a点和b点连接起来)
AcWing 859. Kruskal算法求最小生成树
题目描述
给定一个n个点m条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G = ( V , E ) G=(V,E)G=(V,E),其中V表示图中点的集合,E表示图中边的集合,n=∣V∣,m=∣E∣。
由V 中的全部n 个顶点和E 中n−1 条边构成的无向连通子图被称为G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图G 的最小生成树。
输入格式
第一行输入整数n和m。
接下来m行,每行包含三个整数u,v,w,表示点u和点v之间存在一条权值为w的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出impossible。
数据范围
1 ≤ n ≤ 10^5,
1 ≤ m ≤ 2*10^5,
输入样式:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样式:
6
模板代码:
#include五、二分图:染色法、匈牙利算法
(一)简述

若无向图G=

图论中的一个重要性质:一个图是二分图,当且仅当图中不含奇数环
奇数环,指的是这个环中边的个数是奇数。
可以用染色法来判断一个图是否是二分图,使用深度优先遍历,从根节点开始把图中的每个节点都染色,每个节点要么是黑色要么是白色(2种),每条边两侧的点的颜色不能相同,只要染色过程中没有出现矛盾,说明该图是一个二分图,否则,说明不是二分图。
(二)具体算法
1、染色法
染色法:是用来判断一个图是否是二分图的
染色法是通过深度优先遍历实现
时间复杂度是 O(n+m), n 表示点数,m 表示边数
模板代码:
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色
// u表示当前节点,c表示当前点的颜色
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i]) // 遍历当前节点的邻边
{
int j = e[i];
if (color[j] == -1) // 如果j未染色
{
if (!dfs(j, !c)) return false; // 给j的相邻点染色
}
else if (color[j] == c) return false; // 如果邻边颜色和当前边颜色相同,则出错——————不是二分图
}
return true;
}
bool check()
{
memset(color, -1, sizeof color);
bool flag = true; // 默认可以染色
for (int i = 1; i <= n; i ++ ) // 给n个点的所有相邻点都尝试染色
if (color[i] == -1) // 如果i未染色
if (!dfs(i, 0)) // 给i这个点染白色,如果在这个期间出错了
{
flag = false;
break;
}
return flag;
}
例题:
AcWing 860. 染色法判定二分图
2、匈牙利算法
时间复杂度是 O(nm), n 表示点数,m 表示边数
匈牙利算法:是用来求二分图的最大匹配的
什么是最大匹配:
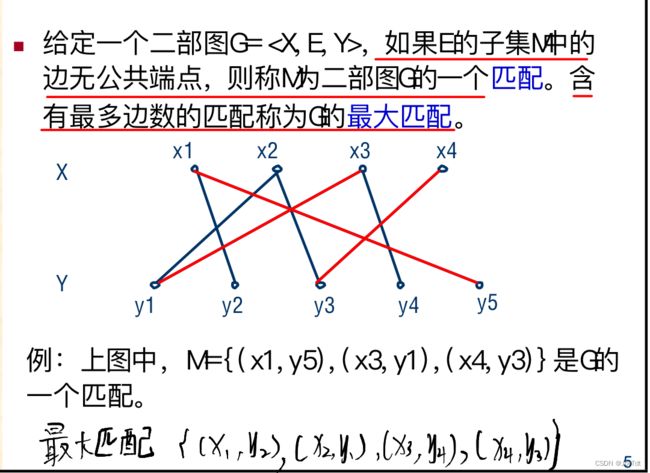
文字定义:给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边,都不依附于同一顶点,则称M是一个匹配。就是每个点只会有一条边相连,没有哪一个点,同时连了多条边。
所有匹配中包含边数最多的一组匹配,被称为二分图的最大匹配。其边数即为最大匹配数
核心思想:
1、依此遍历左侧节点,每次找到当前左侧节点所连接的所有右侧节点,并遍历右侧这些节点
2-a、当右侧的节点没有和其他左侧节点匹配时,直接将这个节点和当前的左边节点匹配。则该左侧节点配对成功
2-b、当右侧节点已经和其他左侧节点匹配上了,则尝试给这个右侧节点所匹配的左侧节点,看能不能让他换一个可以匹配的节点(寻找另一个和这个节点连接的右侧节点),称之为备用节点。如果这个右侧节点所匹配的左侧节点有其他可选择的备用节点。则将这个左侧节点和其备用节点匹配。然后将这个右侧节点和当前节点匹配。
模板代码:
#include例题:
AcWing 861.二分图的最大匹配