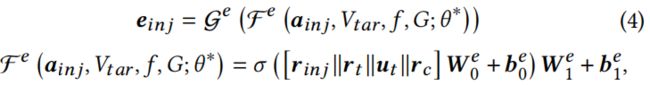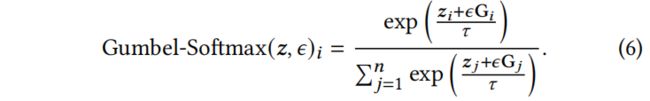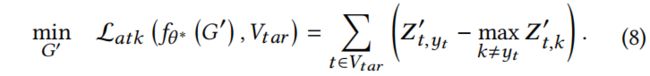CIKM2021《Single Node Injection Attack against Graph Neural Networks》论文详解

原文链接：https://arxiv.org/pdf/2108.13049.pdf

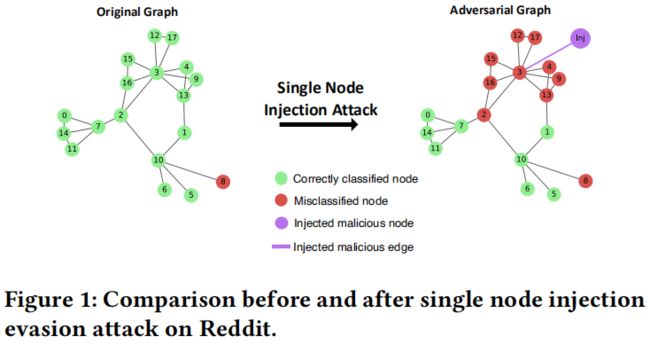
evasion attack

1 Abstract and Introduction

图神经网络节点注入攻击是一种新兴而实用的攻击场景，攻击者通过注入恶意节点而不是修改原始节点或边来影响图神经网络的性能。本文关注的是一个非常有限的单节点注入 evasion attack 场景，即攻击者在测试阶段只被允许注入单个节点来伤害 GNN 的性能。网络结构的离散性以及网络结构与节点特征之间的耦合效应给这种极其有限的场景带来了极大的挑战。本文首先提出了一种基于优化的方法来探讨单节点注入 evasion 攻击的性能上限。然而，这种基于优化的方法需要对每次攻击进行重新优化，这在计算上是无法承受的。为了解决这一难题，进一步提出了一个可泛化节点注入攻击模型 G-NIA，在保证攻击性能的同时提高攻击效率。

现有的节点注入攻击忽略了非常有限的对抗攻击场景，即注入的节点可能过多以至于被目标受害系统或目标节点都能感知或检测到。此外，现有的节点注入攻击一般集中在 poisoning 场景，即假设目标 GNN 对注入的带标签的恶意节点进行训练/再训练。这种假设很难在实际场景中得到满足，因为我们可能不知道目标受害者系统的标签标准。

单节点注入规避（evasion）攻击具有检测难度大、成本低等优点。其关键是将恶意属性随网络结构的变化传播到适当的节点。

本文首先提出了一种基于优化的方法，即 OPTI，来探讨单节点注入 evasion 攻击的性能上限。然而，每次攻击都需要对 OPTI 进行重新优化，这在计算上是无法承受的。此外，每次优化过程中学习到的信息都被丢弃了，阻碍了注入攻击的泛化。

为了解决这一难题，本文进一步提出了一个可泛化节点注入攻击模型 G-NIA，在保证攻击性能的同时提高攻击效率。G-NIA 也通过使用 Gumbel-Top-k 来像 OPTI 一样生成离散边，并通过一个复杂的设计模型捕捉网络结构和节点特征之间的耦合效应。与 OPTI 相比，G-NIA在以下两个方面具有优势。一是表现能力。G-NIA 通过联合建模明确地为最关键的特征传播建模。具体来说，利用恶意属性来指导边的生成，更好地建模属性和边的影响。二是效率高。G-NIA 采用了基于模型的框架，在模型训练过程中利用了攻击的有用信息，在推理过程中无需重新优化，节省了大量的计算成本。

本文方案的主要优点：

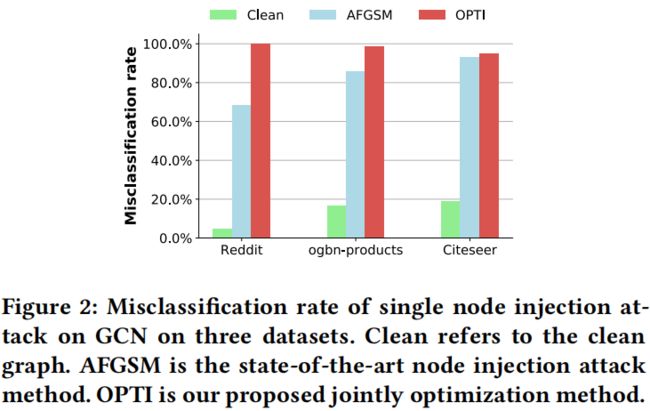
（1）Effectiveness：当只注入一个节点和一条边时，OPTI 可以在社会网络，共同购买网络和引文网络上实现100%，98.60%， 94.98%的成功攻击。G-NIA 可以在推理过程中获得相当的结果，而无需像 OPTI 那样进行重新优化。在这三个数据集上，这两种方法都明显优于目前最先进的方法。

（2）Efficiency：G-NIA 在推理阶段的速度大约比 OPTI 快500倍。

（3）Flexibility：为了证明本文所提出的 G-NIA 模型的有效性，在两种场景下，在三种著名的 GNN 模型上对三种网络数据集进行了大量的实验。此外，G-NIA 还可以在黑盒场景中使用。

2 Related Work

此前有一些在原图上进行修改的方法。但在现实世界中，由于无法访问存储图数据的数据库，修改现有的边或属性是棘手的。节点注入攻击关注的是一种更实际的场景，它只注入一些恶意节点，而不修改已有的图。此前的的研究主要集中在节点注入 poisoning 攻击上，存在一些在 evasion 攻击场景中不可忽视的问题。目前还缺乏一种同时考虑注入节点属性和结构的有效方法。

3 Preliminary

Node Classification. 给定属性图，表示 n 个节点的集合。是 d 维特征的属性矩阵。把网络结构表示为邻接矩阵。给定由标签集标记的节点，目标是通过分类器为每个未标记的节点分配标签，是概率分布，是类别的数量。

 Graph Neural Networks. 典型的 GNN 层包含一个特征变换和一个聚合操作：

 

 其中和是一个 GNN 层维和维的输入和输出特征。特征变换把变换为；特征聚合通过聚合后的特征来更新特征。不同的 GNNs 对和由不同的定义。以 GCN 为例，其中，是度矩阵。是特征变换的权重矩阵。

 3.2 Problem Definition

单节点注入 evasion 攻击的目标是在极其有限的情况下使原始节点错误分类，如在测试阶段，攻击者只允许注入单个节点，而不修改原图中已有的节点和边。将目标函数形式化为：

 

其中是指示函数；是目标节点，可以是单节点也可以是多节点；是节点 t  的真实标签；是在原图上经过训练的被攻击的 GNN 模型。被扰动的图包括恶意注入节点，是该节点的边，是其属性。是连接操作。为了确保不被感知，定义注入边的预算，如。恶意属性还受限于连续属性图的现有属性的最大值和最小值，以及离散属性图的最大范数。

Notes：指示函数：

Eq.(2) 意味着通过在原图中训练得到的参数用在注入节点后的模型中，使得分类器对目标节点的预测尽可能不标签不同。

节点注入 evasion 攻击利用特征传播的优势，将恶意属性传播到合适的节点，而无需重新训练。特征传播依赖于属性和边的耦合效应。因此，核心是在考虑注入节点之间的耦合效应的同时，生成合适的节点属性和边。然而，生成属性和边面临各自的挑战。

Challenges：对于边来说，挑战来自于边的离散性。由此产生的不可微性阻碍了反向传播梯度来指导注入边的优化。对于属性，不同的网络数据集差异很大。大多数网络，如社交网络和共同购买网络，都具有连续属性来表示更多的含义，而研究中常用的引文网络具有离散节点属性来表示关键词的出现。但到目前为止，对连续属性图的研究还很少。离散属性图的生成也面临着与边生成相同的挑战。值得注意的是，没有一种节点注入攻击方法能够同时处理这两种属性图。

 4 Optimization-based Node Injection Attack

4.1 Optimization-based Approach

针对单节点注入 evasion 攻击问题，提出了一种基于优化的方法，即 OPTI，直接优化恶性节点的属性和边。具体来说，首先将恶性属性和边初始化为自由变量，并将它们注入到原图中。然后，将扰动图输入到一个代理 GNN 模型中以获得输出。然后，根据公式（8）计算损失，并对自由变量进行优化，直到收敛。联合优化有助于描述恶性节点的属性与边之间的耦合效应。为了克服上文提到的离散变量的梯度挑战，采用 Gumbel-top-k 来帮助优化。

 4.2 Attack Performance

对三个数据集进行了单节点注入 evasion 攻击。对于每次攻击，攻击者在推理（测试）阶段只注入一个节点和一条边来攻击一个目标节点。将整个图中的每个节点分别选择为目标节点。

结果表明，OPTI 能够成功攻击几乎所有的目标节点。同时也验证了单节点注入 evasion 攻击的可行性和有效性，因此在该攻击场景下无需注入更多节点。

虽然 OPTI 取得了很好的效果，但在现实中却很难实施。因为它是一种个案（case-by-case）方法，这意味着对每次攻击执行不同的优化。优化的计算成本很高，而且没有知识可以保存和重用。更糟糕的是，在图对抗学习领域中，几乎所有的攻击方法都存在这些局限性。因此，是时候探讨单节点注入攻击的有效性了。

5 Generalizable Node Injection Attack

5.1 Generalization in Graph Adversarial Attack

上述基于优化的方法几乎不可能处理现实生活中的攻击，即使它获得了极好的攻击性能。因为 case-by-case 的优化带来的巨大计算量是无法忍受的。为了解决这一难题，提出用一个可推广的模型来模拟优化过程。该模型可以成功地攻击看不见的新鲜节点，只要这些节点服从独立相同分布的假设。

5.2 Framework of Generalizable Node Injection Attack Model

下图展示了 G-NIA 的整体框架。上半部分是 G-NIA 训练阶段的工作流。具体来说，G-NIA 由三部分组成：属性生成，边生成和优化。前两部分为恶意的注入节点生成合适的属性和边，最后一个对代理 GNN 进行攻击，并计算损失以优化 G-NIA。下半部分展示了 G-NIA 如何在测试阶段对原图进行攻击。G-NIA 首先生成恶意的属性，然后生成边，并使用得到的对抗图来攻击目标节点。

 5.3 Attribute Generation

 在节点注入 evasion attack 中，属性对攻击性能是至关重要的，因为属性给成功的攻击带来了额外的信息。

攻击的目标是使目标节点被错误分类，这与目标节点以及类信息（包括标签类），如；以及被代理 GNN 误分类的类别，即相关。目标节点提供了要攻击对象的必要信息，类信息告诉了进行攻击的可能方式，如把预测标签从改为。基于这些，采用目标节点的表示，以及标签类和误分类的表示（即）来生成属性。对于目标节点的表示，由代理 GNN 来表示。在一个两层的 GNN 中，对于标签类，采用特征变换权重的第列，即和，其中。因为特征变换是属性空间和标签空间的映射。

有了上面的表示，使用两层神经网络和一个映射函数来生成恶意注入节点的属性：

 

其中是可训练的参数。把神经网络的输出映射到原图指定的属性空间，使得这个属性与已有节点相似。对于离散属性，包含一个 sigmoid 函数和一个扩展到指定属性空间的标量。对于离散属性，是一个 Gumbel-Top-k 技术。

Notes：这里的两层神经网络就是一个 MLP，对于连续属性，把 MLP 得到的属性与属性最值之差相乘然后加上最小值。

与其他方法相比，G-NIA 更加灵活。本文的模型可以处理离散属性图和连续属性图的高维属性生成，但 AFGSM 只能处理离散属性，NIPA 甚至不能生成属性。

5.4 Edge Generation

恶意边帮助恶意节点将其属性扩展到所需的候选节点。在这里，候选节点被限制在目标节点及其一阶邻域内，使得注入节点至少是目标节点的二阶邻域。因为大多数具有良好性能的 GNN 包含两层特征传播。由于注入边预算 Δ 有限，对候选节点进行评分，并选择最优的 Δ 个候选节点连接到注入的节点。候选节点得分用来衡量某些候选节点连接到恶意节点对攻击性能的影响。

Notes：好像在代码中目标节点的一阶邻域也包括目标节点本身，但却没有排除。

5.4.1 Joinitly modeling. 为了捕获网络结构和节点特征的耦合效应，对恶意属性和边联合建模。具体来说，使用恶意属性来指导恶意边的生成，将注入节点的属性和边联合建模。据此，使用候选节点和恶意节点的表示、来获得评分。由代理 GNN 的特征变换计算得到，如，因为恶意节点还没有结构。（图3中棕色箭头从恶意属性输入到边生成。）

正如前面提到的，攻击的目标与两个元素，目标节点和类信息密切相关。上面两个元素的表示，即和，也包含在神经网络的输入中，两个都重复 m 次，其中 m 为候选节点数。

在上述所有输入的基础上，采用两层神经网络来获取候选节点的得分，并使用 Gumbel-Top-k 技术将得分离散化，如下所示：

 

其中是可训练的参数。 

5.4.2 Gumbel-Top-k technique. 为了解决网络结构的离散性，采用 Gumbel-Top-k 技术来解决边的优化问题。Gumbel 分布用来模拟各种分布的若干个样本的极值分布。形式上，，其中是均匀分布。Gumbel-Softmax：

 

其中是一个用来控制平滑程度的温度系数，是神经网络的输出。Gumbel- softmax 通过 Gumbel 分布对边选择进行探索。为了鼓励探索，进一步使用来控制探索强度：

 

Gumbel-Top-k 函数：

 

其中 k 是边（离散属性）的预算，过滤选中的边/属性，以确保不会再次被选中。注意，获得的向量是锐利的，但不是完全离散的，这有利于训练。在测试阶段，强制离散向量以获得离散边。对于离散属性也是这样。

Gumbel-Top-k 技术可以解决高维离散属性的优化问题。此外，Gumbel-Top-k 并不影响训练的稳定性。

5.5 Optimization

生成恶意属性和边后，将恶意节点注入到原图中，得到扰动图。将输入到代理 GNN 模型中，计算攻击损失：

攻击损失用来指导训练过程。通过梯度下降迭代优化攻击损失，直到收敛。

思考

对于度数比较大的节点，可以通过注入多个节点来改变其预测结果。该图只适合于相对较小的图，对于大型图、度数比较高的节点可能会有问题。注入节点的属性是否可以通过目标节点周围节点的概率平均得到？除了 Gumbel 分布外，还有其它分布适合离散域吗？

欢迎讨论和指教。