集中趋势度量:分散性、变异性、强大的距
作者 白宁超
2015年10月14日10:13:13
摘要:程序员眼中的统计学系列是作者和团队共同学习笔记的整理。首先提到统计学,很多人认为是经济学或者数学的专利,与计算机并没有交集。诚然在传统学科中,其在以上学科发挥作用很大。然而随着科学技术的发展和机器智能的普及,统计学在机器智能中的作用越来越重要。本系列统计学的学习基于《深入浅出统计学》一书(偏向代码实现,需要读者有一定基础,可以参见后面PPT学习)。正如(吴军)先生在《数学之美》一书中阐述的,基于统计和数学模型对机器智能发挥重大的作用。诸如:语音识别、词性分析、机器翻译等世界级的难题也是从统计中找到开启成功之门钥匙的。尤其是在自然语言处理方面更显得重要,因此,对统计和数学建模的学习是尤为重要的。最后感谢团队所有人的参与。( 本文原创,转载注明出处:集中趋势度量:分散性、变异性、强大的距 )
目录
【程序员眼中的统计学(1)】 信息图形化:第一印象
【程序员眼中的统计学(2)】集中趋势度量:分散性、变异性、强大的距
【程序员眼中的统计学(3)】概率计算:把握机会
【程序员眼中的统计学(4)】离散概率分布的运用:善用期望
【程序员眼中的统计学(5)】排列组合:排序、排位、排
【程序员眼中的统计学(6)】几何分布、二项分布及泊松分布:坚持离散
【程序员眼中的统计学(7)】正态分布的运用:正态之美
【程序员眼中的统计学(8)】统计抽样的运用:抽取样本
【程序员眼中的统计学(9)】总体和样本的估计:进行预测
【程序员眼中的统计学(10)】假设检验的运用:研究证据
【程序员眼中的统计学(11)】卡方分布的应用
【程序员眼中的统计学(12)】相关与回归:我的线条如何?
1 平均值
1.1 均值算法的描述
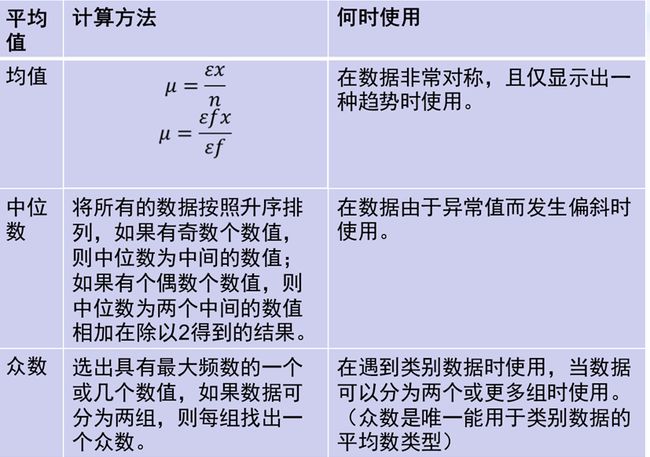
均值的定义
均值有两种计算方法:第一种计算方式是:将所有的数字加起来,然后除以数字的个数 。可用记为:µ=∑x/n
另一种计算方法是把每个数的频数考虑进去了的,它表示如下:µ=∑fx/f
均值符号定义
n:表示的是输入的数据的个数
µ:为数据的均值
∑:表示所有数据之和
均值算法中的计算方法
- 统计出输入数据的个数n
- 计算出所有的数据之和 sum
- 计算出数据的均值avg=sum/n
1.2 均值算法的应用场景
案例描述:俱乐部中,各个舞蹈班的人数的清单为:1人,2人,3 人,4人,5人,6人,7人。
均值算法在该场景的定义
案例定义:这个俱乐部舞蹈班的总人数为28,总共有7个舞蹈班,知道了总的人数和总共有多少个班级,即可求出舞蹈班人数的均值。
该场景下算法中符号解释
n:用来统计输入的舞蹈班的个数
list:用来存储输入的舞蹈班的人数
sum:表示所有舞蹈班的人数之和
avg:表示n个舞蹈班的人数的均值
该场景下算法计算方法
案例中俱乐部舞蹈班的人数的总和为:sum=1+2+3+4+5+6+7,sum=28,
统计出俱乐部中舞蹈班级的个数为:n=7
计算出该俱乐部的人数的均值为:avg=sum/n,avg=28/7=4 ,
1.3 本算法优缺点
- 优点:能够快速准确地计算出均值
- 缺点: 在输入的数据过多时,会产出一定的误差。
- 本算法采用的数据类型:本算法适用于double数据类型。
1.4 算法的输入数据、中间结果以及输出
本算法输入数据
* @param i double,表示输入的数据
* @param list List,存储输入的数据
算法中间结果
* @param sum double,表示输入的所有的数据之和
本算法输出结果
* @return avg double,表示数据的均值
1.5 算法中的异常及处理办法
本算法可能异常或误差
异常1:输入数据不合法,如:输入字母。
异常2:输入数据特别大,会产生误差。
本算法异常或误差处理
异常1:解决,输入不合法给予提示。
异常2:解决,扩大数据占有的空间
1.6 算法的代码参考
源码:
/**
* @Title: set
* @Description: 数据赋值
* @param a存储的是输入的数据
* @author cy
* @date 2015-7-29
*/
public static void set(double a[]) {
b = a;
n=a.length;
}
/**
* @Title: avg
* @Description: 计算平均值
* @param a存储输入的数据
* @param sum 表示输入的所有的数据之和
* @param avg表示数据的均值
* @author cy
* @date 2015-7-29
*/
public static void avg(double a[]) {
// 定义一个平均值、和
double sum = 0;
for (double i : a) {
sum += i;
}
System.out.println("平均值为:" + sum / n);
}类和方法基本描述
类源码:见源程序:Average.java
该算法首先接受输入的n个数据(输入时以输入0为结束),将其存入到List数组list中,再求出这些数据的总和sum,均值avg=sum/n;
类和方法调用接口
见源程序:Average.java
Average.java下包含如下方法:
List
set(List
avg(List
2 中位数值
2.1 中位数算法的描述
中位数的定义永远处于一组数据的中间,它是个中间值
中位数均值符号定义
n:表示的是输入的数据的个数
中位数算法中的计算方法
- 按顺序排列数字:从最小值排列到最大值
- 如果有奇数个数值,则中位数为位于中间的数值。如果有n个数,则中间数的位置为(n+1)/2
- 如果有偶数个数值,则将两个中间数相加,然后除以2.中间位置的算法是:(n+1)/2。两个中间数分别位于这个中间数位置的两侧
2.2 中位数算法的应用场景
案例描述:有两组数据,分别求出两组数据的中位数,并比较两组数据的中位数的情况。
| 年龄 |
19 |
20 |
21 |
147 |
145 |
| 频数 |
3 |
6 |
3 |
1 |
1 |
1 1 1 2 2 2 2 3 3 31 31 32 32 32 32 33 33 33
中位数算法在该场景的定义
案例定义:将两组数据输入到算法中,算法中用数组list接受,之后,算法就会自动的算出这两组数据的中位数。
该场景下算法中符号解释
n:用来统计输入数据个数
list:用来存储输入数据
该场景下算法计算方法
①按顺序排列数字:
1 1 1 2 2 2 2 3 3 31 31 32 32 32 32 33 33 33
②如果有奇数个数值,则中位数为位于中间的数值。如果有n个数,则中间数的位置为(n+1)/2:
③如果有偶数个数值,则将两个中间数相加,然后除以2.中间位置的算法是:(n+1)/2:
该组数据中有18个数据为偶数。因此,用③中的方法,求出该组数据的中位数是17
2.3 本算法优缺点
- 优点:能够快速准确地计算出数据的中位数
- 缺点: 在输入的数据过多时,会产出一定的误差。
- 本算法适用于double数据类型。
2.4 算法的输入数据、中间结果以及输出
本算法输入数据
* @param i double,表示输入的数据
本算法中间结果
* @param list List,存储输入的数据
本算法输出结果
* @return med double,表示数据的中位数
2.5 算法中的异常及处理办法
本算法可能异常或误差
异常1:输入数据不合法,如:输入字母。
异常2:输入数据特别大,会产生误差。
本算法异常或误差处理
异常1:解决,输入不合法给予提示。
异常2:解决,扩大数据占有的空间
2.6 算法的代码参考
源码:
/**
* @Title: med
* @Description: 找中位数
* @param a存储输入的数据
* @param med表示中位数
* @param n表示中位数的个数
* @author cy
* @date 2015-7-29
*/
public static void med(double a[]) {
// 定义中位数
double med;
// 对数据进行排序
Arrays.sort(a);
// 数据个数为奇数的情况
if (n % 2 == 1) {
med = a[(n+1)/2];
// 数据个数为偶数的情况
} else {
med = (a[n / 2 ] + a[n/2+1]) / 2.0;
}
System.out.println("该组数据的中位数为:" + med);
}类和方法基本描述
类源码:见源程序:Median.java
算法中首先按输入的数据存入到数组List中(输入时以输入0为结束),再讲数组中的数字顺序排列:从最小值排列到最大值,如果有奇数个数值,则中位数为位于中间的数值。如果有n个数,则中间数的位置为(n+1)/2,如果有偶数个数值,则将两个中间数相加,然后除以2.中间位置的算法是:(n+1)/2。两个数分别位于这个中间数位置的两侧。
类和方法调用接口
见源程序:Median.java
Median.java下包含如下方法:
List
set(List
med(List
3 众数
3.1 众数算法的描述
众数的定义
众数:即频率最大的数,与均值和中位数不同,众数必须是数据集中的一个数值,而且是最频繁出现的数值。
众数符号定义
n:表示的是输入的数据的个数
众数算法中的计算方法
众数的三步法:
- 把数据中的不同类别或数值全部找出来。
- 写出每个数值或类别的频数。
- 挑出具有最高频数的一个或几个数值,得出众数。
3.2 众数算法的应用场景
案例描述:有一组数据,求出这组数据的众数。
| 年龄 |
19 |
20 |
21 |
147 |
145 |
| 频数 |
3 |
6 |
3 |
1 |
1 |
众数算法在该场景的定义
案例定义:将这组数据输入到算法中,算法中用数组map接受,之后,算法就会自动的算出这组数据的众数。
该场景下算法中符号解释
n:用来统计输入的值个数
map:用来存储输入的值和值出现的频数
tm:存储频数
max:表示最大的频数的值
该场景下算法计算方法
①首先按照要求将上述的数据输入到算法中,并以输入两个#号为结束。
②将输入的数据的频数存储到数组tm中
③找出tm数组中最大的数
④输出tm中与max值相同的数,即为要求的众数。
3.3 本算法优缺点
- 优点:能够快速准确地计算出众数
- 缺点: 在输入的数据过多时,会产出一定的误差。
- 本算法适用于double数据类型,String类型。
3.4 算法的输入数据、中间结果以及输出
本算法输入数据
* @param i double,表示输入的数据
* @param map Map,存储输入的值和该值出现的次数
本算法中间结果
* @param tm int[],存储值得频数
* @param max int 存储频数的最大值
本算法输出结果
* @return int,表示数据的众数
3.5 算法中的异常及处理办法
本算法可能异常或误差
异常1:输入数据特别大,会产生误差。
本算法异常或误差处理
异常1:解决,扩大数据占有的空间
3.6 算法的代码参考
源码:
// 用于统计输入了多少数据
static int n = 0;
static String a1[];
static int b1[];
/**
* @Title: set
* @Description: 数据赋值
* @param a存储输入的数值,b数值出现的次数
* @author cy
* @date 2015-7-29
*/
public static void set(String a[],int b[]) {
a1=a;
b1=b;
n=b.length;
}
/**
* 找众数
* @param n输入的数据的个数
* @param b存储数值出现的次数的数组
* @param max表示次数的最大值
*/
public static void zs(String a[],int b[]) {
int i = 0;
Arrays.sort(b);
// 数组b中的最大值
int max;
// 获取数组中的最大值
max = b[b.length - 1];
System.out.print("众数为:");
for (int j =0;j类和方法基本描述
类源码:见源程序:Mode.java
算法中利用Map(映射,集合中的每一个元素包含一对键对象和值对象,键对象对应数据中的数值,值对象对应数值出现的频数)来存储输入的数据,将数据存入到map中,以输入两个#为输入结束。将map中的值对象即频数读出存入到数组tm中,在对数组tm进行排序,求出数组tm中的最大值max,最后将所有的最大值输出即得到众数。
类和方法调用接口
见源程序:Mode.java
Mode.java下包含如下方法:
Map
set(Map
zs(Map
4 方差
4.1 方差算法的描述
方差的定义
方差:量度数据分散性的一种方法,是数据与均值的距离的平方数的平值。
方差公式:∑(x-μ)^2/n
方差符号定义
n:表示的是输入的数据的个数
u:为数据的均值
∑:表示所有数据之和
方差算法中的计算方法
n:表示的是输入的数据的个数
u:为数据的均值
∑:表示所有数据之和
4.2 方差算法的应用场景
案例描述:有一组数据,求出这组数据的方差情况。
1 1 1 2 2 2 2 3 3 31 31 32 32 32 32 33 33 33
方差算法在该场景的定义
案例定义:将这组数据输入到算法中,算法中用数组list接受,之后,算法就会先计算出这一组数据的均值,再统计出该组数据的个数,最后,计算出这组数据的方差。
该场景下算法中符号解释
n:用来统计输入的数据个数
list:用来存储输入数据
sum:表示所有的数据之和
u:表示n个数据的均值
该场景下算法计算方法
案例中数据的和:sum=306 ,
统计数据的个数为:n=18
计算出该组数据的均值为:avg=sum/n,avg=17 ,
再计算出该组数据的方差为226.4083044982699
4.3 本算法优缺点
- 优点:能够快速准确地计算出方差
- 缺点: 在输入的数据过多时,会产出一定的误差。
- 本算法适用于double数据类型。
4.4 算法的输入数据、中间结果以及输出
本算法输入数据
* @param i double,表示输入的数据
* @param list List,存储输入的数据
本算法中间结果
* @param sum double,表示输入的所有的数据之和
* @param n int,表示输入的数据的个数
* @param u double表示数据的平均值
本算法输出结果
* @return fc double,表示数据的方差
4.5 算法中的异常及处理办法
本算法可能异常或误差
异常1:输入数据不合法,如:输入字母。
异常2:输入数据特别大,会产生误差。
本算法异常或误差处理
异常1:解决,输入不合法给予提示。
异常2:解决,扩大数据占有的空间
4.6 算法的代码参考
源码:
/**
* @Title: calFac
* @Description: 计算方差
* @param a存储输入的数据
* @param sum1所有的数据之和
* @param u所有的数据的均值
* @author cy
* @date 2015-7-29
*/
public static double calFac(double a[]) {
// 数据的平均值
double u;
// 存储数据之和
double sum1 = 0;
for (double s : a) {
sum1 += s;
}
// 计算平均值
u = sum1 / n;
for (double s : a) {
sum = sum + (s) * (s);
}
return (sum / n - u * u);
}
/**
* @Title: fac
* @Description: 输出方差
* @param a存储输入的数据
* @author cy
* @date 2015-7-29
*/
public static void fac(double a[]) {
System.out.println("方差为:" + calFac(a));
}
类和方法基本描述
类源码:见源程序:Facha.java
方差算法的描述:方差是数据与均值的距离的平方数的平值。该算法首先接受输入的n个数据(输入时以输入0为结束),将其存入到List数组list中,再求出这些数据的总和sum,再求出数据的均值u=sum/n;最后根据方差的快速计算公式得出方差的值。
类和方法调用接口
见源程序:Facha.java
Facha.java下包含如下方法:
List
set(List
5 标准差
5.1 标准差算法的描述
标准差的定义
标准差:是描述典型值与均值距离的一种方法,标准差越小,数值离均值越近 。
标准差公式:σ=方差开方
注:标准差也有可能为0,如果每个数值与均值的距离都是为0,则标准差将为0。
标准差符号定义
n:表示的是输入的数据的个数
u:为数据的均值
∑:表示所有数据之和
σ:表示标准差
标准差算法中的计算方法
1、计算出该组数据的均值u
2、再统计该组数据的个数n
3、利用方差的公式计算出方差
4、利用标准差的公式计算出标准差
5.2 标准差算法的应用场景
案例描述:有一组数据,求出这组数据的标准差情况。
1 1 1 2 2 2 2 3 3 31 31 32 32 32 32 33 33 33
标准差算法在该场景的定义
案例定义:将这组数据输入到算法中,算法中用数组list接受,之后,算法就会先计算出这一组数据的均值,再统计出该组数据的个数,计算出这组数据的方差,最后计算出该组数据的标准差。
该场景下算法中符号解释
n:用来统计输入的数据个数
list:用来存储输入数据
sum:表示所有的数据之和
u:表示n个数据的均值
该场景下算法计算方法
案例中数据的和:sum=306,
统计数据的个数为:n=18
计算出该组数据的均值为:avg=sum/n,avg=17 ,
再计算出该组数据的方差为226.408304498269
最后计算出该组数据的标准差:15.129074290546956
5.3 本算法优缺点
- 优点:能够快速准确地计算出标准差
- 缺点: 在输入的数据过多时,会产出一定的误差。
- 本算法适用于double数据类型。
5.4 算法的输入数据、中间结果以及输出
本算法输入数据
** @param i double,表示输入的数据
* @param list List,存储输入的数据
本算法中间结果
* @param sum double,表示输入的所有的数据之和
* @param n int,表示输入的数据的个数
* @param u double表示数据的平均值
本算法输出结果
* @return bzc double,表示数据的方差
5.5 算法中的异常及处理办法
本算法可能异常或误差
异常1:输入数据不合法,如:输入字母。
异常2:输入数据特别大,会产生误差。
本算法异常或误差处理
异常1:解决,输入不合法给予提示。
异常2:解决,扩大数据占有的空间
5.6 算法的代码参考
源码:
/**
* @Title: fac
* @Description: 计算标准差
* @param a存储输入的数据
* @param sum1所有的数据之和
* @param u所有的数据的均值
* @author cy
* @date 2015-7-29
*/
public static void bzc(double a[]){
double bzc;
// 计算方差
bzc = calFac(a);
// 标准差=方差开根号
System.out.println("标准差为:" + Math.sqrt(bzc));
}
类和方法基本描述
类源码:见源程序:Bzc.java
该算法首先接受输入的n个数据(输入时以输入0为结束),将其存入到List数组list中,再求出这些数据的总和sum,再求出数据的均值u=sum/n;最后根据方差的快速计算公式得出方差的值,将方差的值开根号即得到标准差的值。
类和方法调用接口
见源程序:Bzc.java
Bzc.java下包含如下方法:
List
set(List
bzc(List
6 本章补充
6.1 基本概念
全距
全距:也叫极差,是用于来量度数据集分散程度的一种方法。
其算法为:上界减去下界,其中上界为最大值,下界为最小值。
- 优点:全距是量度数据分散程度的既简单又方便的方法。
- 缺点:全距仅仅描述了数据的宽度,并没有描述数据在上下界之前的分布形态,不能体现数据的实际分布形态。并且,全距很容易受到异常值的影响。
摆脱异常值的办法:四分位数
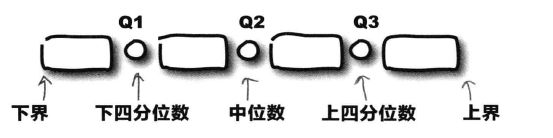
四分位法:它将数据一分为四,最小的四分位数称为下四分位数,最大的四分位数称为上四分位数,中间的四分位数即为中位数。
四分位距=上四分位数-下四分位数
求下四分位数的位置
①首先计算n/4
②如果结果为整数,则下四分位数位于“n/4”这个位置和下一个位置的中间取这两个位置上的数值的平均值,即得到下四分位数。
③如果“n/4”不是整数,则向上取整,结果即为下四分视为数的位置。
例如:如果你有6个数,首先计算6/4,得到1.5.向上取整的得到2,这表示下四分数的位置为2.
求上四分位数的位置
①首先计算3n/4
②如果结果为整数,则上四分位数位于“3n/4”这个位置这个位置和下一位置的中间,取这两个位置上的数值的平均值,即得到上四分位数。
③如果“3n/4”不是整数,则向上取整,所得到的新数字即为上四分位数的位置。
百分位数:是将数据一分为百的数值。
箱线图
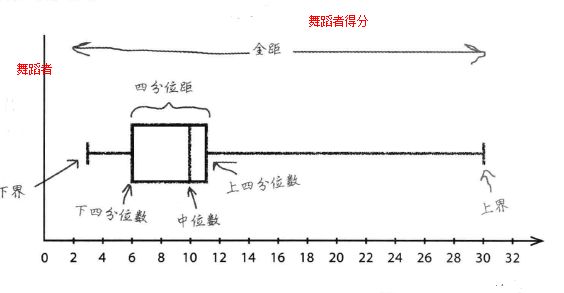
用箱线图绘制各种“距”
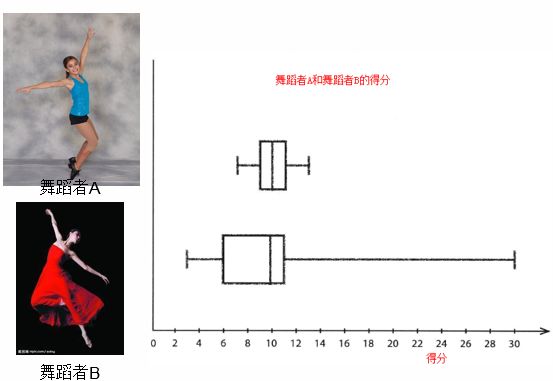
创建箱线图:首先按标度画出一个“箱”,想的左右两边分布代表下四分位数和上四分位数,然后在箱中画出一条线,标示中位数,这个箱的宽度就是四分距的宽度,随后,在箱的两边画出“线”,显示出全距的上界、下界和宽度。以下就是之前提到的舞蹈者的得分的箱线图。
舞蹈者A的全距相对较小,她的得分中位数比舞蹈者B的高一些,舞蹈者B的全距非常大,有时候这位舞蹈者的得分比舞蹈者A高很多,但是有时又低很多,舞蹈者A发挥更稳定,通常得分高于舞蹈者B,所以,我们会选择舞蹈者A
标准分
标准分是对不同环境下的相关数据进行比较的一种方法,可以对不同数据集的数据进行比较,可以使用标准分比较舞蹈者相对于其本人历史纪录的表现。
标准分的计算公式:z=(x-μ)/σ
计算标准分:
6.2 小结
学习的统计量:均值、中位数、众数,它们只是让我们知道了数据中心的情况,即数据集中的典型的具有代表性的数值,而第三章学的知识对让我们对一个数据集有了更完整的了解,知道了数据集中数值的实际的分布形态,有助于我们对数据更好的掌握。
本章主要讲的是分散性和变异性的量度,分散性的量度主要有全距(容易受异常值的影响)、四分位距(摆脱了异常值得影响)。异常性的量度主要有方差、标准差、标准分