数据结构-栈和队列

目录

栈

什么是栈

 栈的实现

队列

什么是队列

 队列的实现

栈

什么是栈

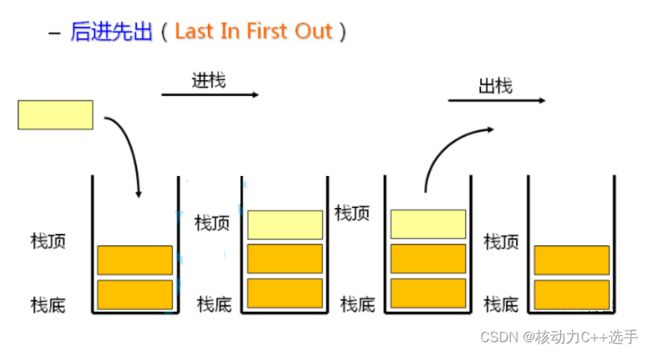
所谓栈，是一种特殊的线性表，只允许在固定的一端进行插入删除操作。进行数据插入删除的一端叫做栈顶，另一端叫做栈底，栈中的数据遵循先入后出的原则。

压栈：栈的数据插入操作叫做压栈，压栈是在栈顶插入数据。

出栈：栈的数据删除操作叫做出栈。出栈是在栈顶删除数据。

 栈的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

接下来我们以数组的方式实现栈。

我们先来用一个结构体定义栈：

typedef struct Stack
{
	STDataType* a;
	int capacity;
	int top;//标识栈顶位置
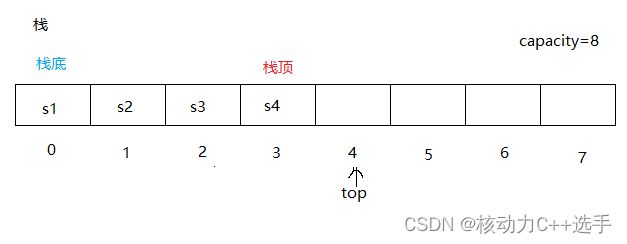
}ST;

其中，a是在堆上开辟数组的地址，capacity表示当前栈的容量，top标识栈顶位置。

接下来，我们设计栈的初始化函数：

void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->capacity = 0;
	//表示指向栈顶元素的下一个位置
	pst->top = 0;
	//表示top指向栈顶位置
	//pst->top = -1;
}

需要注意的是，这里的top在初始化时，如果初始化为0，则top指向栈顶的下一个元素；如果初始化为-1，则top指向栈顶元素。

接下来，设计栈的销毁函数，由于栈中的数组元素是在堆上开辟的，因此要进行释放，否则会造成内存泄漏：

void STDestory(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;
	pst->capacity = 0;
	pst->top = 0;
}

接下来，我们设计栈插入和删除函数：

首先是栈插入函数：

void STPush(ST* pst, STDataType x)
{
	assert(pst);
	if (pst->capacity == pst->top)
	{
		int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;
		STDataType* tmp = (STDataType*)realloc(pst->a,newcapacity * sizeof(STDataType));
		pst->capacity = newcapacity;
		if (tmp == NULL)
		{
			perror("realloc");
			return;
		}
		pst->a = tmp;
	}
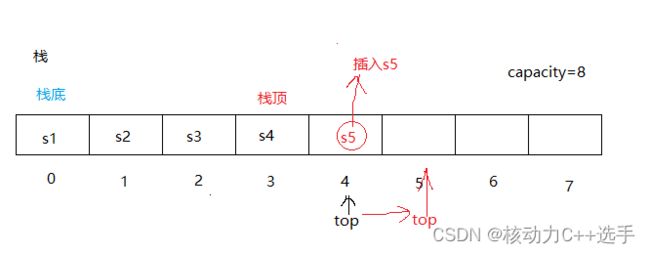
	pst->a[pst->top] = x;
	pst->top++;
}

 由于我在初始化栈时，top设成0，因此，把待插入的元素x放到数组pst->top的位置，然后pst->top++，指向栈顶的下一个元素。

接着是栈删除函数：

void STPop(ST* pst)
{
	assert(pst);
	//不为空
	assert(pst->top > 0);
	pst->top--;
}

将top--即可。

接下来，我们设计取栈顶元素函数：

STDataType STTop(ST* pst)
{
	assert(pst);
	//不为空
	assert(pst->top > 0);

	return pst->a[pst->top - 1];
}

由于pst->top表示栈顶的下一个元素，因此栈顶元素为pst->top-1位置的元素。

接下来设计判断栈是否为空的函数：

bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
}

如果pst->top==0，那么表示栈里没有元素（如果最开始初始化栈时top==-1，那么当pst->top==-1时，才表示栈里没有元素）

接下来设计返回栈元素个数函数：

int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

pst->top不但表示栈顶下一个元素，也表示栈中元素的个数。

队列

什么是队列

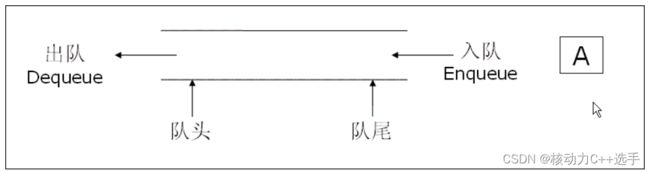
所谓队列，只允许在一端插入数据，在另一端删除数据，并且具有先进先出的特点。

入队列：进行插入数据的一端称为队尾

出队列：进行删除数据的一端称为队头

 队列的实现

考虑到数组在删除队头数据时比较麻烦，因此，我打算基于单向链表实现队列。

对于链表的每一个结点，都有两个成员，一个是val，另一个是指向下一个结点的指针：

typedef int QDataType;

typedef struct QueneNode
{
	QDataType val;
	struct QueneNode* next;
}QNode;

为了便于队列的实现，定义了Quene这个结构体：

typedef struct Quene
{
	QNode* phead;
	QNode* ptail;
	int size;
}Quene;

这个结构体维护了一个队列，结构体中的phead和ptail分别指向队列的头尾，同时size记录队列的长度，以便在需要时可以知道此时队列的长度。

在main函数中，定义了Quene q;这个结构体变量；

接下来，我们首先要设计q的初始化函数：

void QueneInit(Quene* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;

	pq->size = 0;
}

这个函数让q的phead和ptail都指向空，同时q的size为0。

接着，当我们退出程序前，肯定要销毁我们创建的队列结点，否则会造成内存泄漏：

void QueneDestroy(Quene* pq)
{
	assert(pq);

	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

接着，我们设计给队列插入元素的函数，创建了一个结点newnode，然后进行尾插。

void QuenePush(Quene* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc");
		return;
	}

	newnode->val = x;
	newnode->next = NULL;

	if (pq->ptail == NULL)
	{
		pq->phead = pq->ptail = newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}

	pq->size++;

}

 然后，设计给队列删除元素的函数：

void QuenePop(Quene* pq)
{
	assert(pq);
	assert(pq->phead);

	QNode* del = pq->phead;
	pq->phead = pq->phead->next;
	free(del);
	del = NULL;

	if (pq->phead == NULL)
		pq->ptail = NULL;

	pq->size--;
}

 需要注意的是，如果把队列中的最后一个元素删除后，pq->tail就是野指针了，所以需要认为将pq->tail置空。

接着，我设计取出队列头尾结点数据的函数，这个就比较简单：

QDataType QueneFront(Quene* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->phead->val;
}

QDataType QueneBack(Quene* pq)
{
	assert(pq);
	assert(pq->phead);

	return pq->ptail->val;
}

然后，再设计判断队列是否为空的函数：

bool QueneEmpty(Quene* pq)
{
	assert(pq);
	
	return pq->ptail == NULL;
}

当队列为空，返回true；否则，返回false。（当使用布尔值时，需要包含stdbool头文件）

最后，设计返回队列元素个数的函数：

int QueneSize(Quene* pq)
{
	assert(pq);
	return pq->size;
}