python3中的heapq模块(堆排序)使用
一. heapq介绍
heapq-堆排序算法:heapq实现了一个适合与Python的列表一起使用的最小堆排序算法。
1. 二叉树
2. 满二叉树
3. 完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。

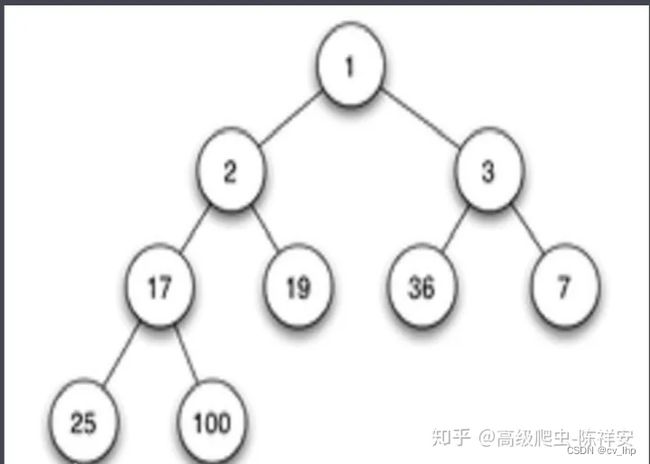
4. 堆
堆是一种数据结构,它是一颗完全二叉树。最小堆则是在堆的基础增加了新的规则,它的根结点的值是最小的,而且它的任意结点的父结点的值都小于或者等于其左右结点的值。因为二进制堆可以使用有组织的列表或数组来表示,所以元素N的子元素位于位置2 * N + 1和2 * N + 2。这种布局使重新安排堆成为可能,因此在添加或删除项时不需要重新分配那么多内存。
区分堆(heap)与栈(stack):堆与二叉树有关,像一堆金字塔型泥沙;而栈像一个直立垃圾桶,一列下来。
5. 最大堆
最大堆确保父节点大于或等于它的两个子节点。
6. 最小堆
最小堆要求父节点小于或等于其子节点。Python的heapq模块实现了一个最小堆。
7. 总结
堆就是用数组表示的二叉树,分为大根堆和小根堆,大根堆为堆顶元素最大的堆,小根堆为堆顶元素最小的堆

二. 使用
1. heappush(heap,item)建立大、小根堆
heapq.heappush()是往堆中添加新值,此时自动建立了小根堆,代码如下:
import heapq
a = [] #创建一个空堆
heapq.heappush(a,18)
heapq.heappush(a,1)
heapq.heappush(a,20)
heapq.heappush(a,10)
heapq.heappush(a,5)
heapq.heappush(a,200)
print(a)
输出:
[1, 5, 20, 18, 10, 200]
但heapq里面没有直接提供建立大根堆的方法,可以采取如下方法:每次push时给元素加一个负号(即取相反数),此时最小值变最大值,反之亦然,那么实际上的最大值就可以处于堆顶了,返回时再取负即可。
a = []
for i in [1, 5, 20, 18, 10, 200]:
heapq.heappush(a,-i)
print(list(map(lambda x:-x,a)))
输出:
[200, 18, 20, 1, 10, 5]
2. heapify(heap)建立大、小根堆
heapq.heapfiy()是以线性时间将一个列表转化为小根堆(复杂度O(logn)):
a = [1, 5, 20, 18, 10, 200]
heapq.heapify(a)
print(a)
输出:
[1, 5, 20, 18, 10, 200]
用上面同样的方法建立大根堆:
a = [1, 5, 20, 18, 10, 200]
a = list(map(lambda x:-x,a))
heapq.heapify(a)
print([-x for x in a])
输出:
[200, 18, 20, 5, 10, 1]
与上面所得大根堆相比,虽然二叉树的第三层元素顺序不同,但都符合大根堆的定义:
3. heappop(heap)
使用heappop()弹出并返回堆中的最小项,保持堆不变。如果堆是空的,则引发IndexError。
heapq.heappop()是从堆中弹出并返回最小的值
3.1 利用heappop进行堆排序
堆排序当然也要利用到heappush或者heapify,可参考排序算法总结中的堆排序,这里只贴代码:
import heapq
def heap_sort(arr):
if not arr:
return []
h = [] #建立空堆
for i in arr:
heapq.heappush(h,i) #heappush自动建立小根堆
return [heapq.heappop(h) for i in range(len(h))] #heappop每次删除并返回列表中最小的值
若是从大到小排列,有两种方法:
1)先建立小根堆,然后每次heappop(),此时得到从小到大的排列,再reverse。
2)利用相反数建立大根堆,然后heappop(-元素)。即push(-元素),pop(-元素)
3.2 普通list的heappop()
普通list(即并没有进行heapify等操作的list),对他进行heappop操作并不会弹出list中最小的值,而是弹出第一个值:
>>> a=[3,6,1]
>>> heapify(a) #将a变成堆之后,可以对其操作
>>> heappop(a)
1
>>> b=[4,2,5] #b不是堆,如果对其进行操作,显示结果如下
>>> heappop(b) #按照顺序,删除第一个数值并返回,不会从中挑选出最小的
4
>>> heapify(b) #变成堆之后,再操作
>>> heappop(b)
2
4. heappushpop(heap,item)
heapq.heappushpop()是heappush和heappop的结合,同时完成两者的功能,先进行heappush(),再进行heappop()
>>>h = heapq.heapify([1, 2, 9, 5])
>>> heappop(h)
1
>>> heappushpop(h,4) #增加4同时删除最小值2并返回该最小值,与下列操作等同:
2
>>> h
[4, 5, 9]
5 heapreplace(heap, item)弹出并返回 heap 中最小的一项,同时推入新的 item
heapq.heapreplace()与heapq.heappushpop()相反,先进行heappop(),再进行heappush()。
堆的大小不变。 如果堆为空则引发 IndexError。这个单步骤操作比依次执行heappop() + heappush() 更高效,并且在使用固定大小的堆时更为适宜。
pop/push 组合总是会从堆中返回一个元素并将其替换为 item。返回的值可能会比添加的 item 更大。 如果不希望如此,可考虑改用 heappushpop()。 它的 push/pop 组合会返回两个值中较小的一个,将较大的值留在堆中。
>>> a=[]
>>> heapreplace(a,3) #如果list空,则报错
Traceback (most recent call last):
File "" , line 1, in <module>
IndexError: index out of range
>>> heappush(a,3)
>>> a
[3]
>>> heapreplace(a,2) #先执行删除(heappop(a)->3),再执行加入(heappush(a,2))
3
>>> a
[2]
>>> heappush(a,5)
>>> heappush(a,9)
>>> heappush(a,4)
>>> a
[2, 4, 9, 5]
>>> heapreplace(a,6) #先从堆a中找出最小值并返回,然后加入6
2
>>> a
[4, 5, 9, 6]
>>> heapreplace(a,1) #1是后来加入的,在1加入之前,a中的最小值是4
4
>>> a
[1, 5, 9, 6]
6 merge(*iterables)
heapq.merge()合并多个堆然后输出,
输入的list无序,merge后无序,若输入的list有序,merge后也有序
7. nlargest(n , iterbale, key=None) 和nsmallest(n , iterbale, key=None)
获取列表中最大、最小的几个值,key的作用和sorted( )方法里面的key类似:
>>>a = [0, 1, 2, 3, 4, 5, 5, 7, 8, 10, 15, 20, 25]
>>>heapq.nlargest(5,a)
[25, 20, 15, 10, 8]
>>>b = [('a',1),('b',2),('c',3),('d',4),('e',5)]
>>>heapq.nlargest(1,b,key=lambda x:x[1])
[('e', 5)]
8. 复杂度分析
8.1 各方法复杂度
1)heapq.heapify(x): O(n)
2)heapq.heappush(heap, item): O(logn)
3)heapq.heappop(heap): O(logn)
即插入或删除元素时,所有节点自动调整,保证堆的结构的复杂度为O(log n)
4)heapq.nlargest(k,iterable) 和 heapq.nsmallest(k,iterable):O(n * log(t))
8.2 关于排序和取TopN时各方法的快慢比较
在关于排序和取Top N值时,到底使用什么方法最快,python3 cookbook给出了非常好的建议:
1)当要查找的元素个数相对比较小的时候,函数nlargest() 和 nsmallest()。
2)仅仅想查找唯一的最小或最大(N=1)的元素的话,那么使用min()和max()函数。
3)如果N的大小和集合大小接近的时候,通常先排序这个集合然后再使用切片操作会更快点 (sorted(items)[:N] 或者是 sorted(items)[-N:])。
9. 利用heapq模块实现优先队列
# priority 优先级
class PriorityQueue:
def __init__(self):
self._queue = []
self._index = 0
def push(self, item, priority):
# heappush 在队列 _queue 上插入第一个元素
heapq.heappush(self._queue, (-priority, self._index, item))
self._index += 1
def pop(self):
# heappop 在队列 _queue 上删除第一个元素
return heapq.heappop(self._queue)[-1]
class Item:
def __init__(self, name):
self.name = name
def __repr__(self):
return ‘Item({!r})’.format(self.name)
1)调用push()方法,实现将列表转化为堆数据
2)插入的是元组,元组大小比较是从第一个元素开始,第一个相同,再对比第二个元素,我们这里采用的方案是如果优先级相同,那么就根据第二个元素,谁先插入堆中,谁的index就小,那么它的值就小
3)heapq.heappop() 方法得到,该方法会先将第一个元素弹出来,然后用下一个最小的元素来取代被弹出元素。
测试:
q = PriorityQueue()
q.push(Item(‘foo’), 1)
q.push(Item(‘bar’), 5)
q.push(Item(‘spam’), 4)
q.push(Item(‘grok’), 1)
print(q.pop())
print(q.pop())
print(q.pop())
输出:
Item(‘bar’)
Item(‘spam’)
Item(‘foo’)
10. 堆输出打印
import math
from io import StringIO
def show_tree(tree, total_width=36, fill=' '):
"""Pretty-print a tree."""
output = StringIO()
last_row = -1
for i, n in enumerate(tree):
if i:
row = int(math.floor(math.log(i + 1, 2)))
else:
row = 0
if row != last_row:
output.write('\n')
columns = 2 ** row
col_width = int(math.floor(total_width / columns))
output.write(str(n).center(col_width, fill))
last_row = row
print(output.getvalue())
print('-' * total_width)
print()
import heapq
from heapq_showtree import show_tree
from heapq_heapdata import data
heap = []
print('random :', data)
print()
for n in data:
print('add {:>3}:'.format(n))
heapq.heappush(heap, n)
show_tree(heap)
输出结果:
random : [19, 9, 4, 10, 11]
add 19:
19
------------------------------------
add 9:
9
19
------------------------------------
add 4:
4
19 9
------------------------------------
add 10:
4
10 9
19
------------------------------------
add 11:
4
10 9
19 11
------------------------------------
三. 参考链接
- Python中heapq模块浅析
- python3中的heapq模块使用

