python 单因子方差分析_Python数据科学：方差分析

之前已经介绍的变量分析：

①相关分析：一个连续变量与一个连续变量间的关系。

②双样本t检验：一个二分分类变量与一个连续变量间的关系。

本次介绍：

方差分析：一个多分类分类变量与一个连续变量间的关系。

其中分类个数大于两个，分类变量也可以有多个。

当分类变量为多个时，对分类个数不做要求，即可以为二分分类变量。

/ 01 / 数理统计技术

数理统计分为频率和贝叶斯两大学派。

描述性统计分析，描述性分析就是从总体数据中提炼变量的主要信息，即统计量。

描述性分析的难点在于对业务的了解和对数据的寻找。

统计推断和统计建模，建立解释变量与被解释变量之间可解释的、稳定的、最好是具有因果关系的表达式。

在模型运用时，将解释变量(自变量)带入表达式中，用于预测被解释变量(因变量)的值。

现阶段，我学习的就是统计推断与建模的知识...

/ 02 / 方差分析

方差分析用于检验多个样本的均值是否有显著差异。

探索多于两个分类的分类变量与连续变量的关系。

比如说「浅谈数据分析岗」中薪水与教育程度之间的关系，教育程度为一个多分类的分类变量。

01 单因素方差分析

单因素方差分析的前提条件：

①变量服从正态分布(薪水符合)。

②观测之间独立(教育程度符合)。

③需验证组间的方差是否相同，即方差齐性检验。

组间误差与组内误差、组间变异与组内变异、组间均方与组内均方都是方差分析中的衡量标准。

如果组间均方明显大于组内均方，则说明教育程度对薪水的影响显著。

那么需要大多少才能确定结论呢？

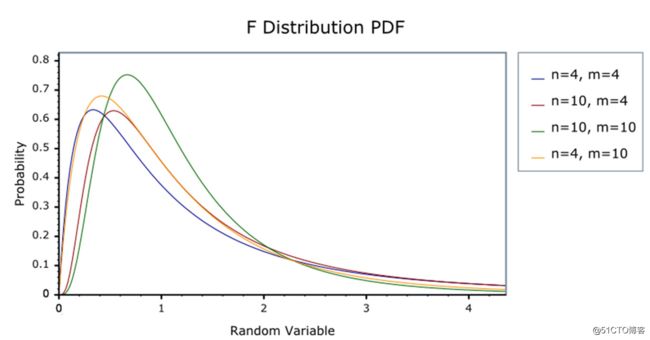
这里组间均方与组内均方的比值是服从F分布，下面贴出F分布曲线图。

其中横坐标为F值，即组间均方与组内均方的比值。

当F值越大时，即组间均方越大、组内均方越小，说明组间的变异大。

并且对应的P值也越小(纵轴)，便可以拒绝原假设(原假设为无差异)。

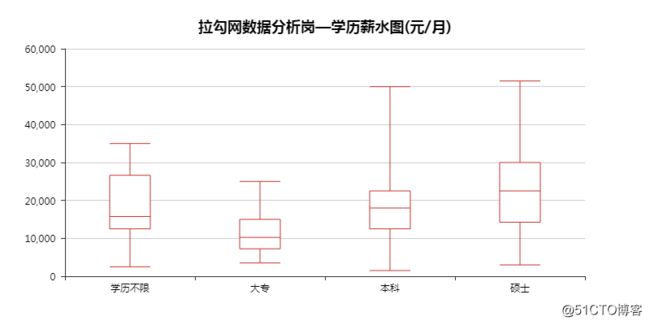
下面以「浅谈数据分析岗」中薪水与教育程度为例。

这里我们只是直观的看出薪水随学历的增长而增长，并没有实实在在的东西。

接下来就用数字来说话！！！

代码如下，需要清洗数据。

from scipy import stats

import pandas as pd

import pymysql

# 获取数据库数据

conn = pymysql.connect(host='localhost', user='root', password='774110919', port=3306, db='lagou_job', charset='utf8mb4')

cursor = conn.cursor()

sql = "select * from job"

df = pd.read_sql(sql, conn)

# 清洗数据,生成薪水列

dom = []

for i in df['job_salary']:

i = ((float(i.split('-')[0].replace('k', '').replace('K', '')) + float(i.split('-')[1].replace('k', '').replace('K', ''))) / 2) * 1000

dom.append(i)

df['salary'] = dom

# 去除无效列

data = df[df.job_education != '不限']

# 生成不同教育程度的薪水列表

edu = []

for i in ['大专', '本科', '硕士']:

edu.append(data[data['job_education'] == i]['salary'])

# 单因素方差分析

print(stats.f_oneway(*edu))

# 得到的结果

F_onewayResult(statistic=15.558365658927576, pvalue=3.0547055604132536e-07)

得出结果，F值为15.5，P值接近于0，所以拒绝原假设，即教育程度会显著影响薪水。

02 多因素方差分析

多因素方差分析检验多个分类变量与一个连续变量的关系。

除了考虑分类变量对连续变量的影响，还需要考虑分类变量间的交互效应。

这里由于我的数据满足不了本次操作，所以选择书中的数据。

即探讨信用卡消费与性别、教育程度的关系。

首先考虑无交互效应，代码如下。

import statsmodels.formula.api as smf

import statsmodels.api as sm

import pandas as pd

# 读取数据,skipinitialspace:忽略分隔符后的空白,dropna:对缺失的数据进行删除

df = pd.read_csv('creditcard_exp.csv', skipinitialspace=True)

df = df.dropna(how='any')

# smf:最小二乘法,构建线性回归模型,

ana = smf.ols('avg_exp ~ C(edu_class) + C(gender)', data=df).fit()

# anova_lm:多因素方差分析

print(sm.stats.anova_lm(ana))

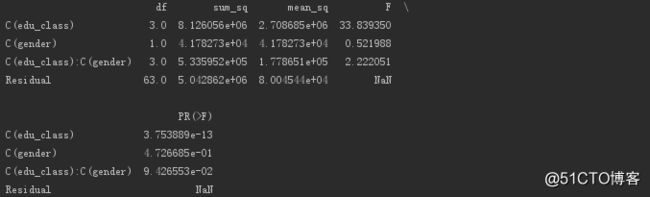
输出结果。

可以看到教育程度的F值为31.57，P值趋近于0，拒绝原假设，即教育程度与平均支出有显著差异。

性别的F值为0.48，P值为0.48，无法拒绝原假设，即性别与平均支出无显著差异。

接下来考虑有交互效应，代码如下。

# 消除pandas输出省略号情况

pd.set_option('display.max_columns', 5)

# smf:最小二乘法,构建线性回归模型

anal = smf.ols('avg_exp ~ C(edu_class) + C(gender) + C(edu_class)*C(gender)', data=df).fit()

# anova_lm:多因素方差分析

print(sm.stats.anova_lm(anal))

输出结果。

这里可以看出，考虑交互效应后，与教育程度及性别对应的F值和P值都发生了微小的改变。

其中教育程度和性别的交互项对平均支出的影响也是显著的，F值为2.22，P值为0.09。

上面这个结论是书中所说的，那么显著性水平取的是0.1吗？？？

这算是我理解不了的一部分。

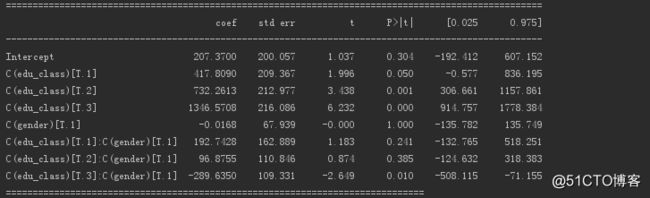
下面是带交互项的多元方差分析的回归系数，表格中所有数据都是以男性及研究生学历作为基准去比对。

# 生成数据总览

print(anal.summary())

输出结果。

可以看出第一种教育程度的女性较男性研究生，信用卡消费的影响较显著，P值为0.05。

原假设为无差异，拒绝原假设。

那么这里的显著性水平取的也是0.1吗？？？

第二种教育程度的女性较男性研究生，信用卡消费的影响显著，P值为0.001。

第三种缺失，没有参数估计。

/ 03 / 总结

这里总结一下各个检验的原假设。

单样本t检验原假设：总体均值与假设的检验值不存在显著差异(无差异)。

双样本t检验原假设：两个样本均值(二分变量下的均值)不存在显著差异(无差异)。

方差分析原假设：多个样本均值(多分变量下的均值)不存在显著差异(无差异)。

说明原假设都是假设变量关系无显著差异。

文末点个赞，比心！！！

···  END  ···