单因素方差分析及其相关检验
ANOVA
单因子方差分析
(1)问题与数据 设某因子有r个水平,记为 ,在每一水平下各做m次独立重复试 验,若记第i个水平下第j次重复的试验结果为 ,所有试验的结果可列表如下:
对这个试验要研究的问题是 个水平 间有无显著差异.
(2) 基本假定
A1 : 第 个水平下的数据 是来自正态总体 的一个样 本
个方差相同 即 ;
A3 : 诸数据 都相互独立. 在这三个基本假定下,要检验的假设是
方差分析就是在方差相等的条件下,对若干个正态均值是否相等的假设检验.
(3)平方和分解式
若记 上述诸平方和分别为
称为总平方和,其自由度 ;
称为组间平方和或因子 的平方和,其自由度
称为组内平方和或误差平方和, 其自 由度 注 : 数据 的平移 不会改变其平方和的值. 用此性质可简化计算.
(4) 方差分析表
(5) 判断 在 成立下, ,对给定的显著性水平 , 其拒绝域为
若 则认为因子 显著,即诸正态均值间有显著差异
数据结构式及其参数估计 (1)数据结构式
其中 为总均值, 为第 个水平的效应, 且 为试验误差,所有 可 作为来自 的一个样本,在上述数据结构式下 要检 验的假设检验可改写为
不全为(2) 点估计
总均值 的估计 ;
水平均值 的估计
主效应 的估计
误差方差 的估计 .
(3) 置信区间
的 置信区间为
首先生成一些虚假的选民年龄和人口统计数据,接着使用方差分析比较各组的平均年龄:
import numpy as np
import scipy.stats as stats
import pandas as pd
np.random.seed(12)
races = ["asian","black","hispanic","other","white"]
# 生成随机数据
voter_race = np.random.choice(a= races,
p = [0.05, 0.15 ,0.25, 0.05, 0.5],
size=1000)
voter_age = stats.poisson.rvs(loc=18,
mu=30,
size=1000)
# 将年龄数据按种族分类
voter_frame = pd.DataFrame({"race":voter_race,"age":voter_age})
groups = voter_frame.groupby("race").groups
voter_frame

groups
{'asian': Int64Index([ 4, 7, 14, 21, 49, 53, 59, 78, 95, 98, 135, 136, 162,
203, 227, 264, 278, 289, 326, 335, 345, 373, 430, 480, 484, 491,
516, 587, 602, 684, 692, 708, 715, 761, 776, 826, 828, 832, 853,
897, 942, 951, 986, 996],
dtype='int64'),
'black': Int64Index([ 0, 9, 19, 22, 23, 42, 50, 56, 62, 76,
...
948, 956, 961, 965, 968, 972, 982, 984, 989, 990],
dtype='int64', length=147),
'hispanic': Int64Index([ 2, 10, 24, 28, 31, 32, 38, 40, 44, 45,
...
954, 955, 958, 959, 962, 964, 966, 974, 994, 999],
dtype='int64', length=244),
'other': Int64Index([ 17, 26, 39, 46, 48, 65, 67, 72, 146, 237, 246, 255, 284,
302, 317, 322, 358, 370, 386, 413, 425, 446, 530, 542, 569, 571,
573, 575, 583, 626, 629, 637, 662, 696, 700, 701, 728, 739, 756,
757, 773, 813, 819, 880, 923, 936, 939, 971, 980, 992],
dtype='int64'),
'white': Int64Index([ 1, 3, 5, 6, 8, 11, 12, 13, 15, 16,
...
981, 983, 985, 987, 988, 991, 993, 995, 997, 998],
dtype='int64', length=515)}
# 提取不同种族的年龄信息,进行方差分析
asian = voter_age[groups["asian"]]
black = voter_age[groups["black"]]
hispanic = voter_age[groups["hispanic"]]
other = voter_age[groups["other"]]
white = voter_age[groups["white"]]
stats.f_oneway(asian, black, hispanic, other, white)
F_onewayResult(statistic=1.7744689357329695, pvalue=0.13173183201930463)
检验结果的F统计量为1.774,p值为0.1317,表明各组的平均值之间没有显著差异。
方差分析的另一种方法是使用statsmodels库:
import statsmodels.api as sm
from statsmodels.formula.api import ols
model = ols('age ~ race',
data = voter_frame).fit()
anova_result = sm.stats.anova_lm(model, typ=2)
print (anova_result)
sum_sq df F PR(>F)
race 199.369 4.0 1.774469 0.131732
Residual 27948.102 995.0 NaN NaN
可以看出,statsmodels方法生成的F统计量和P值与stats.Fèoneway方法完全相同。
现在重新进行一次方差检验,修改下年龄数据,使每组的平均值确实不同:
np.random.seed(12)
voter_race = np.random.choice(a= races,
p = [0.05, 0.15 ,0.25, 0.05, 0.5],
size=1000)
# 给白种人的年龄设置一个不同的location
white_ages = stats.poisson.rvs(loc=18,
mu=32,
size=1000)
voter_age = stats.poisson.rvs(loc=18,
mu=30,
size=1000)
voter_age = np.where(voter_race=="white", white_ages, voter_age)
voter_frame = pd.DataFrame({"race":voter_race,"age":voter_age})
groups = voter_frame.groupby("race").groups
asian = voter_age[groups["asian"]]
black = voter_age[groups["black"]]
hispanic = voter_age[groups["hispanic"]]
other = voter_age[groups["other"]]
white = voter_age[groups["white"]]
stats.f_oneway(asian, black, hispanic, other, white)
F_onewayResult(statistic=10.164699828386366, pvalue=4.5613242113994585e-08)
model = ols('age ~ race', # Model formula
data = voter_frame).fit()
anova_result = sm.stats.anova_lm(model, typ=2)
print (anova_result)
sum_sq df F PR(>F)
race 1284.123213 4.0 10.1647 4.561324e-08
Residual 31424.995787 995.0 NaN NaN
测试结果表明,在这种情况下,两组的样本均值并不相同,因为p值在99%的置信水平下是显著的。
多重比较
在单因子方差分析中,当因子 显著时,就要继续研究如下问题 : 在多个水平均值中同时比较任意两个水平间有无明显差异的问题,这个问题的 检验法则称多重比较. 若因子 有 个水平,则同时检验 个假设
其拒绝域 对给定的显著性水平 诸临 界值 由 决定
Turkey 法 在各水平试验次数相同时,其诸临界值 也相 同,具体为
其中 是分布 的 分位数.
from statsmodels.stats.multicomp import pairwise_tukeyhsd
tukey = pairwise_tukeyhsd(endog=voter_age,
groups=voter_race,
alpha=0.05)
tukey.plot_simultaneous() # 画出每组的置信区间
plt.vlines(x=49.57,ymin=-0.5,ymax=4.5, color="red")
tukey.summary()

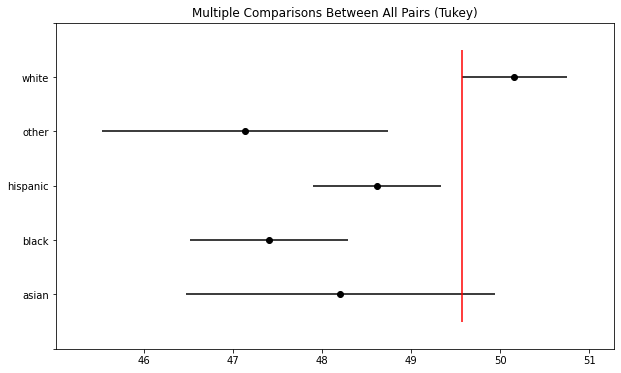
Tukey检验的结果显示了平均差异、置信区间以及在给定显著性水平下是否应该拒绝原假设。在这种情况下,测试结果显示拒绝了3对原假设,每一对均包括“白色”类别。这表明白人群体可能与其他人不同。95%置信区间图显示了只有一个组的置信区间和白色组置信区间有重叠。
方差齐次性检验
问题 方差齐性即诸方差相等,是方差分析的基本假定之一,方差齐性检验就是检验这个假定是否成立. 该检验问题的一对假设为 vs 诸 不全相等.
Hartley 检验,检验统计量是
其中 是第 个水平 下重复试验数据的样本方差. 拒绝域为
其中 为显著性水平 是统计量 的分布的 分位数
Levene检验是Bartlett检验的替代方法。与正常情况相比,Levene检验不如Bartlett检验敏感。如果有确凿的证据表明数据确实来自正态分布或接近正态分布,那么Bartlett的检验将具有更好的性能。检验统计量是
其中: 为第 个样本的含量, 为各样本含量之 和, 为将原 始数据经数据转换后的新的变量值。 为第 个样 本的均数, 。为全部数据的总的均数。拒绝域为
# Bartlett 检验
# scipy官网上的一个例子
from scipy.stats import bartlett
a = [8.88, 9.12, 9.04, 8.98, 9.00, 9.08, 9.01, 8.85, 9.06, 8.99]
b = [8.88, 8.95, 9.29, 9.44, 9.15, 9.58, 8.36, 9.18, 8.67, 9.05]
c = [8.95, 9.12, 8.95, 8.85, 9.03, 8.84, 9.07, 8.98, 8.86, 8.98]
stat, p = bartlett(a, b, c)
p
1.1254782518834628e-05
P值很小,意味着要拒绝原假设,a,b,c的方差不是齐次的
# 求a,b,c各自的方差
[np.var(x, ddof=1) for x in [a,b,c]]
[0.007054444444444413, 0.13073888888888888, 0.008890000000000002]
stat, p = bartlett(asian, black, hispanic, other, white)
p
0.16370899141700943
[np.var(x, ddof=1) for x in [asian, black, hispanic, other, white]]
[24.25951374207189,
33.06383375267915,
37.216268636578285,
30.612653061224485,
29.20417060179064]
# Levene检验
from scipy.stats import levene
a = [8.88, 9.12, 9.04, 8.98, 9.00, 9.08, 9.01, 8.85, 9.06, 8.99]
b = [8.88, 8.95, 9.29, 9.44, 9.15, 9.58, 8.36, 9.18, 8.67, 9.05]
c = [8.95, 9.12, 8.95, 8.85, 9.03, 8.84, 9.07, 8.98, 8.86, 8.98]
stat, p = levene(a, b, c)
p
0.002431505967249681
stat, p = levene(asian, black, hispanic, other, white)
p
0.4355288565481745

