计算机组成原理之定点加法、减法运算详解(含双符号位运算结果溢出处理)
我们利用补码表示负数后,可以将负数当做正数一样来处理,所以在运算器中,加法器就可以完成加法和减法的工作。
补码加法
补码加法的公式是:[x]补+[y]补=[x+y]补 (mod 2n+1)
eg:1.x=+1001,y=+0101,求x+y.
01001
+00101
01110
所以x=y=+1110.
2.x+1011,y=-0101,求x+y.
01011
+11011
00110
所以x+y=+0110.
补码减法
补码减法的公式为:[x-y]补=[x]补-[y]补=[x]补+[-y]补 (mod 2n+1)
其中,从[y]补求[-y]补的法则是:对[y]补包括符号位“求反且最末位加1”,表示为:[-y]补=(求反)[y]补 +2-n.
ps:利用负的真值求补码也可以实现。
eg:1.已知x=-1110,y=+1101,求[x]补,[-x]补,[y]补,[-y]补.
[x]补=10010.
[-x]补=[+1110]补=01110.
[y]补=01101.
[-y]补=[-1101]补=10011.
2.x=+1101,y=+0110,求x-y。
[x]补=01101.
[-y]补=[-0110]补=11010
故[x-y]补=[x]补-[y]补=[x]补+[-y]补=01101+11010=00111=+0111
溢出概念与检测方法
在定点整数运算过程中如出现大于字长绝对值的现象称为“溢出”,在定点机中出现溢出时其结果是不正确的,故运算器必须能检测出溢出。
eg:1.x=+1011,y=+1001,求x+y。
[x]补=01011,[y]补=01001.
01011
+01001
10100
x+y=10100=-0100,这样两正数相加结果是负数,显然是错误的。
2.x=-1101,y=-1011,求x+y。
[x]补=10011,[y]补=10101.
10011
+10101
01000
x+y=01000=+1000,两负数相加结果是正数,同样是错误的。
两个正数相加结果大于机器字长所能表示的最大正数称为正溢;
两个负数相加结果小于机器所能表示的最小负数称为负溢;
为了判断“溢出”是否发生我们采用双符号位法,又称为“变形补码”:
遵循规则:1.两个符号位都看作数码一样参加运算
2.两数进行以2n+2为模的加法,最高符号位上产生的进位要丢掉。
正数:00xxxxx
负数:11xxxxx
如果两数相加后结果的符号位出现“01”或“10”两种组合表示发生溢出(最高符号位永远指示正确的符号)
eg:
1.x=+1100,y=+1000,求x+y。
[x]补=001100,[y]补=001000.
[x+y]补=001100+001000=010100
两符号位数字不同,出现"01",出现正溢出。
这时的正确答案应该是比原来的四位多一位,而最高位永远指示正确的符号,所以答案是x+y=+10100
2.x=-1100,y=-1000,求x+y.
[x]补=110100,[y]补=111000.
[x+y]补=110100+111000=101100
两符号位数字不同,出现“10”,出现负溢出。
最终答案是x+y=-10100【对101100求反+1,得010100(这个是-[x+y]补),真值为+10100,所以x+y真值就为-10100】
这是很好用的方法,体会一下
总结出以下检测方法:
1.以变形补码运算,结果两符号位相异表示溢出,相同表示未溢出。
2.采用单符号位法,最高有效位进位和符号位进位相异或,为真则溢出;也就是说最高有效位进位和符号位进位同时为1或0表示未溢出,否则表示溢出。
二进制加法/减法器
二进制数字Ai,Bi和一个进位输入Ci相加,产生一个和输出Si,以及一个进位输出Ci+1.
这里代入数字模拟流程,了解其底层基本实现原理即可。
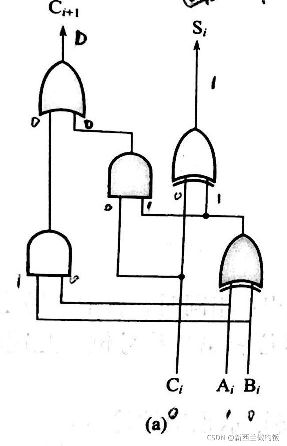
这里用到数字逻辑基础,平底为与门,弯底且无曲线为或门,弯底加曲线为异或门。
对图(a)所示一位全加器来说,求其结果Si的时间延迟为6T(每级异或门为3T,T为一个“与”门或一个“或”门的时间延迟作为度量单位)
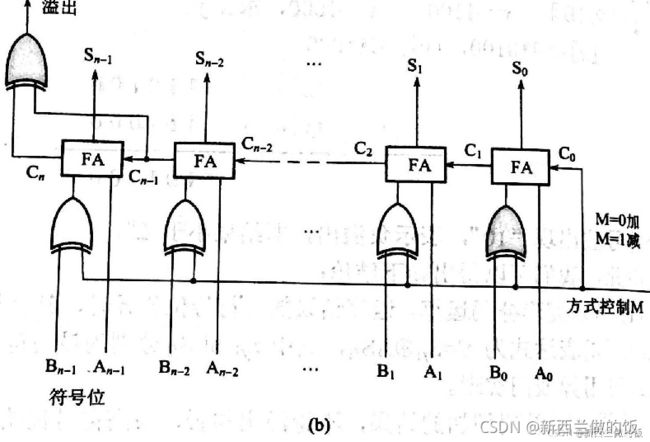
图(b)为n位行波进位加法器,Ci+1的时间延迟为2T。
若采用图a所示的一位全加器并考虑溢出检测,那么n位行波进位加法器的延迟时间ta为ta=n*2T+9T=(2n+9)T.
9T为最低位上两级异或门加上溢出异或门的总时间;2T为每级进位链的延迟时间。