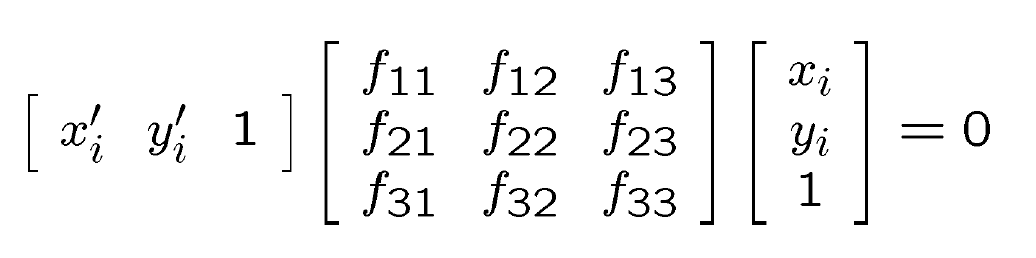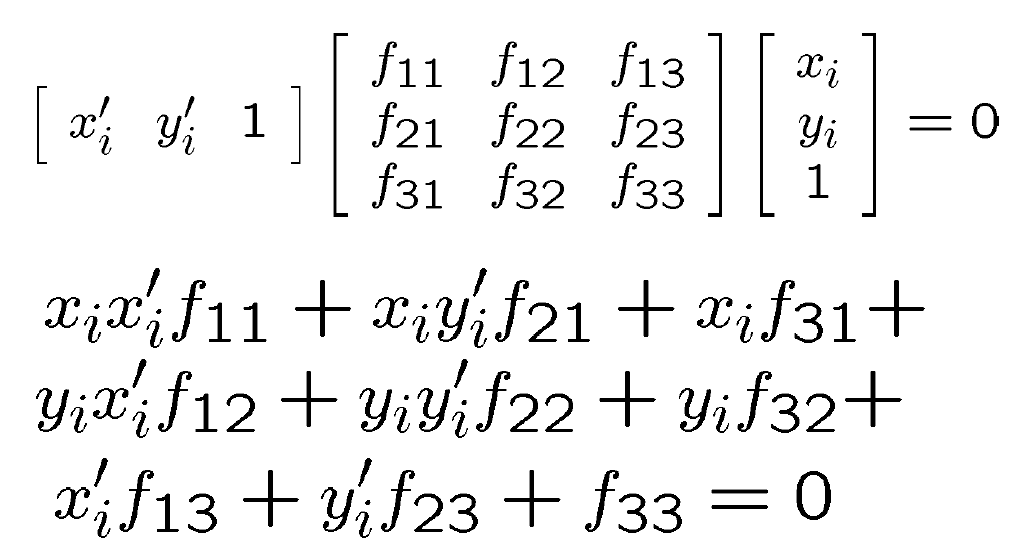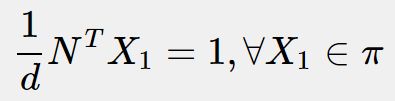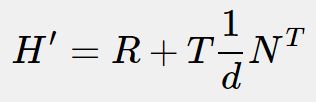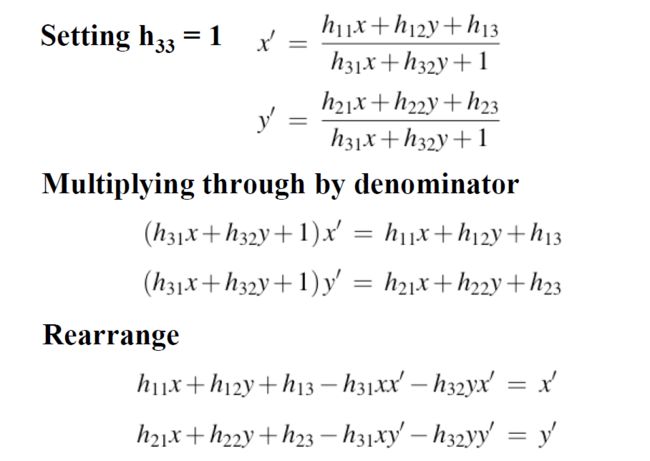对极几何及单应矩阵

1.本质矩阵

用两个相机在不同位置拍摄同一物体，两张照片中的景物有重叠部分，那么理论上这两张照片会存在一定的对应关系，本节任务是探索如何描述他们之间的对应关系--对极几何，属于立体视觉的部分。关于相机成像模型等部分这里不多介绍。

首先来看几个基本概念

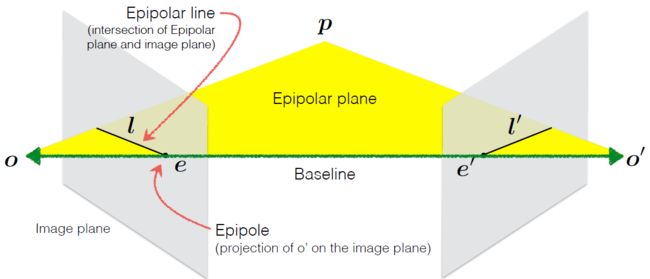
图中的概念有：

极点e：分别是左边相机中心在右图像平面上的像，右相机中心在左像平面上的像。

极平面：两个相机中心和空间中某店p形成的平面。

极线l：极平面分别和两个像平面的交线。

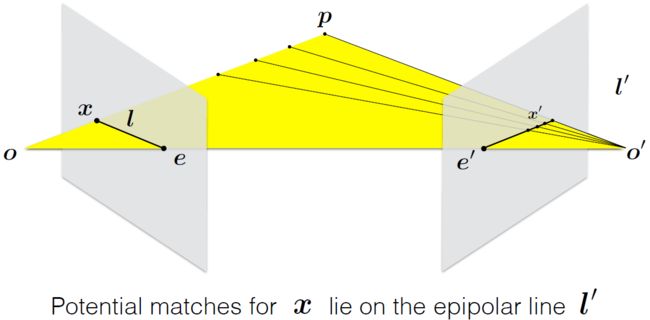
对极几何则是描述这几个量之间的对应关系。直观讲，从左图的角度看，如果不知道p点的深度信息，射线op是这个点可能出现的空间位置，因为该射线上的点都会投影到同一个像素点，同时，如果不知道p点的具体位置，那么当在右图的位置看时，极线 l' 就是点p可能出现的位置，即在这条线上的某个地方。如下图所示

回顾向量的知识

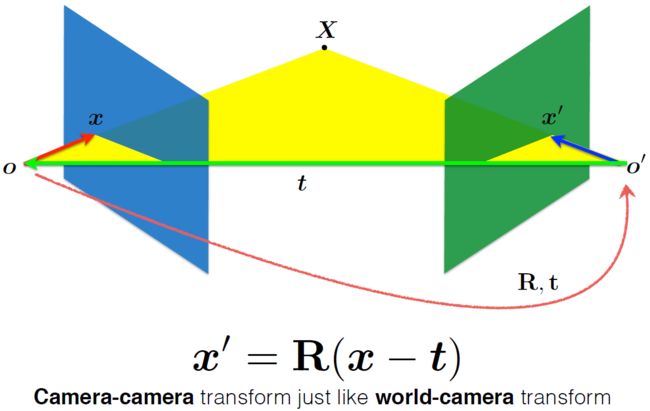
两个正交的向量的内积为0。假设左图到右图的位姿关系由 R 和 t 表示，那么由基本的刚体变换可以得到

另外

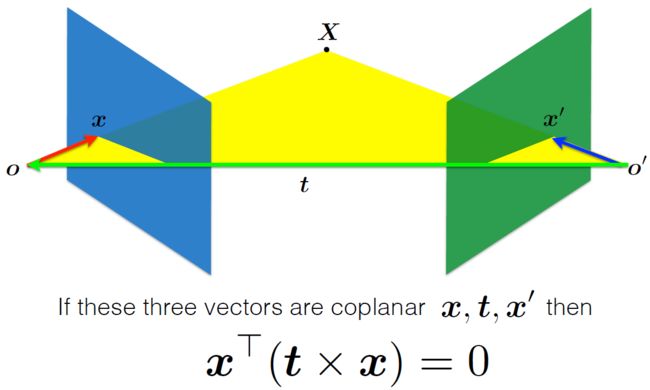
已知三向量 x, t 和 x' 共面，则 t 和 x 做外积得到一个垂直该平面的向量，因此上式为零没有问题，接下来

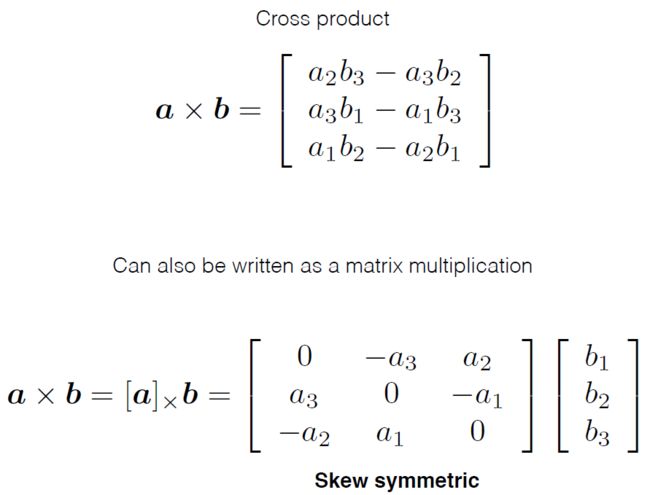
简单的代入即可。然后，向量的外积可以写成矩阵相乘的形式，即将其中一个向量写成反对称矩阵，如下图

那么将之前的 t 和 x 的外积也写成矩阵的形式可得

其中的矩阵E就是本质矩阵，最后一个式子为对极约束，形式非常简洁，描述了不同位置拍摄同一个点时这两个点构成的约束，同时可以看到矩阵E由旋转矩阵R和平移向量t组成，对E进行分解即可得到两幅图像的位姿关系，前提是左右图像中的两个点要正确匹配！！！

注意：这里的左右两个点 x 和 x' 分别为在相机坐标系下的归一化平面上的点，即 x = [x,y,1]，而不是像素平面上的点，因此需首先获得空间点在相机系中的坐标值，之后将其归一化到 z = 1的平面上，才能使用对极约束求解。

前文提到过，对极几何描述的是一个空间点经过对极约束后得到的是其可能出现在第二幅图像中的极线上，这里进行解释：

利用直线的一般方程的知识

当点在直线上时，代入直线方程结果为零。回到对极约束中，这里用 p 代替上文中左右两图中的 x 点

前面说过对极约束中的点是相机系中归一化平面上的点，是三维的点，因此将其和本质矩阵相乘，将得到一个3行1列的向量，而由图可知左图中的点乘以这个向量结果为零，因此可以说点在这个向量构成的直线方程上，同样的

因此，本质矩阵和左像点坐标相乘后得到了一条直线，而该点在右图中的位置就处在这条直线上。本质矩阵和右像点相乘后也得到一条直线，该点在左图中的位置也处在这条直线上。

可以看到：本质矩阵将一个点映射到了一条线上，该点在另一幅图像中可能的位置就在这条线上。

本质矩阵的求解

对极约束是一个等式为零的约束，因此对他乘以非零常数后依然成立，这称为本质矩阵的尺度等价性。另一方面，由于平移和旋转各有三个自由度，故 E 共有六个自由度，但由于尺度等价性，因此实际上 E 具有5个自由度。

即最少可用5对点来求解 E，但是这种解法比较麻烦。考虑 E 的尺度等价性，可以使用8对点来求解，即经典的八点法，八点法利用了 E 的线性性质，因此可以通过线性代数求解。

2.基础矩阵

必须注意本质矩阵描述的是几何意义上的约束，他只是将左右相机内的物理坐标进行了约束。实际处理图像时，最直接得到的是某个点在图像中的像素坐标值，由于像素坐标和归一化坐标通过相机内参矩阵进行联系，因此可得

假设M为相机内参，代入对极约束

上图中 F 矩阵即为基础矩阵，他不光包含了旋转和平移的信息，还包含了相机的内参信息，使用的是像素坐标。

3.单应矩阵

单应是射影几何中的概念，又称为射影变换。他把一个射影平面上的点映射到另一个平面对应的位置，并且把直线映射为直线，具有保线性质。与对极几何不同的是，对极几何将点映射到线上，而单应矩阵是点对点的关系。要注意的是单应矩阵的适用场景为：当场景中的特征点都落在同一平面上，比如墙、地面等，此时可用单应性估计运动。其描述方程为

其中矩阵 H 为一个3x3的非奇异矩阵，且对矩阵 H 乘以非零的常量依然成立

假设已经获得了两幅图像之间的单应矩阵，可得

其中左边为图像1中的点，右边为图像2中的点。其具有很多应用，除了估计运动，还能对图像进行校正，比如斜着拍摄一栋楼，通过单应矩阵，可以生成一张看起来是正对着楼拍摄的照片。

接下来看推导和求解过程

由于是假设特征点处于同一平面，因此首先设平面在第一个相机系下的法向量为 N，深度为 d，则平面方程为

即

X1，X2分别为点在两个相机系下的坐标，因此

将上面两式子结合可得

因此单应矩阵为

可以看到其同样含有旋转和平移信息。

单应矩阵的求解

注意：以上做法只有当 h33  即最后一个元素不为零是才能得到正确的解！

以上可以看出，一对匹配点可以得到两项约束，于是自由度为8的单应矩阵可以通过4对匹配点进行求解

对极约束和单应性

 

• 两幅图像之间的对极约束和场景的结构无关，即对于任意场景结构的图像都是成立的，他不能给出两幅图像上的点的一一对应关系，只能将点映射到线。而单应矩阵可以将点对应到点。
• 单应矩阵，不像对极约束那样完全不限制场景的结构，单应矩阵要求场景中的点都在同一平面上。
• 当相机只有旋转没有平移时，可使用单应矩阵估计运动，因为此时平移为0，计算得到的本质矩阵也为0，进而旋转也为0，得到了错误的解，而使用单应性依然能够正确计算。