C/C++二分查找
文章目录
- 算法解释
- 求开方
-
- 69.X的平方根(Easy)
- 查找区间
-
- 34.在排序数组中查找元素的第一个和最后一个位置
- 数组查找数字
-
- 81.搜索旋转排序数组Ⅱ
- 153.寻找旋转排序数组中的最小值(Medium)
- 154.寻找旋转排序数组中的最小值Ⅱ(Hard)
- 540.有序数组中的单一元素(Medium)
- 4.寻找两个正序数组的中位数(Hard)
- 总结
算法解释
二分查找也常被称为二分法或者折半查找,每次查找时通过将待查找区间分成两部分并只取一部分继续查找,将查找的复杂度大大减少。对于一个长度为 O(n) 的数组,二分查找的时间复杂度为 O(log n)。
举例来说,给定一个排好序的数组 {3,4,5,6,7},我们希望查找 4 在不在这个数组内。第一次折半时考虑中位数 5,因为 5 大于 4, 所以如果 4 存在于这个数组,那么其必定存在于 5 左边这一半。于是我们的查找区间变成了 {3,4,5}。(注意,根据具体情况和您的刷题习惯,这里的 5 可以保留也可以不保留,并不影响时间复杂度的级别。)第二次折半时考虑新的中位数 4,正好是我们需要查找的数字。于是我们发现,对于一个长度为 5 的数组,我们只进行了 2 次查找。如果是遍历数组,最坏的情况则需要查找 5 次。
二分查找也可以看作双指针的一种,但它的指针每次移动半个区间的长度。
求开方
69.X的平方根(Easy)
题目描述
给定一个非负整数,求它的开方,向下取整。
输入输出样例
输入一个整数,输出一个整数
输入:x = 4
输出:2
8 的开方结果是 2.82842…,向下取整即是 2。
代码
class Solution {
public:
int mySqrt(int x) {
if(x==0) return 0;
int l=0,r=x,mid=0,ans=0;
while(l<=r){
mid=l+(r-l)/2;
if((long long)mid*mid<=x){
ans=mid;
l=mid+1;
}else{
r=mid-1;
}
}
return ans;
}
};
查找区间
34.在排序数组中查找元素的第一个和最后一个位置
题目描述
给定一个增序的整数数组和一个值,查找该值第一次和最后一次出现的位置。
输入输出样例
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
题解
这道题可以看作是对C++里面lower_bound和upper_bound函数的实现。
代码
class Solution {
public:
int my_lower_bound(vector<int>& nums,int target){
int l=0,r=nums.size(),mid=0;
while(l<r){
mid=l+(r-l)/2;
if(nums[mid]>=target){
r=mid;
}else{
l=mid+1;
}
}
return l;
}
int my_upper_bound(vector<int>& nums,int target){
int l=0,r=nums.size(),mid=0;
while(l<r){
mid=l+(r-l)/2;
if(nums[mid]>target){
r=mid;
}else{
l=mid+1;
}
}
return l;
}
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size()==0) return {-1,-1};
int lower = my_lower_bound(nums, target);
int upper = my_upper_bound(nums, target) - 1; // 这里需要减1位
if (lower == nums.size() || nums[lower] != target) {
return vector<int>{-1, -1};
}
return vector<int>{lower, upper};
}
};
数组查找数字
81.搜索旋转排序数组Ⅱ
题目描述
一个原本增序的数组被首尾相连后按某个位置断开(如 [1,2,2,3,4,5] → [2,3,4,5,1,2],在第一位和第二位断开),我们称其为旋转数组。给定一个值,判断这个值是否存在于这个为旋转数组中。
输入输出样例
输入是一个数组和一个值,输出是一个布尔值,表示数组中是否存在该值。
输入:nums = [2,5,6,0,0,1,2], target = 0
输出:true
题解
数组被旋转过,我们仍然可以利用这个数组的递增性,来进行二分查找。对于当前的中点,如果它指向的值小于等于右端,那么说明右区间是排好序的;反之,那么说明左区间是排好序的。如果目标值位于排好序的区间内,我们可以对这个区间继续二分查找;反之,我们对于另一半区间继续二分查找。
但是这道题因为数组存在重复数字,如果中点和左端的数字相同,我们并不能确定是左区间全部相同,还是右区间完全相同。在这种情况下,我们可以将左端点右移一位,然后继续进行二分查找。
代码
class Solution {
public:
bool search(vector<int>& nums, int target) {
int l=0,r=nums.size()-1,mid=0;
while(l<=r){
mid=l+(r-l)/2;
if(nums[mid]==target){ //相等则返回ture
return true;
}else {
if(nums[l]==nums[mid]){ //当出现相同数字时,无法分辨,左边界++
++l;
}else if(nums[mid]<=nums[r]){ //右半部分时单增
if(nums[mid]<target&&target<=nums[r]){
l=mid+1;
}else{
r=mid-1;
}
}else{ //左半部分是单增
if(target>=nums[l]&&target<nums[mid]){
r=mid-1;
}else{
l=mid+1;
}
}
}
}
return false;
}
};
153.寻找旋转排序数组中的最小值(Medium)
题目描述
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
输入输出样例
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
题解
主要分为两种情况
代码
class Solution {
public:
int findMin(vector<int>& nums) {
int left=0,right=nums.size()-1,mid=0;
while(left<right){
mid=left+(right-left)/2;
if(nums[mid]<nums[right]){
right=mid;
}else{
left=mid+1;
}
}
return nums[left];
}
};
154.寻找旋转排序数组中的最小值Ⅱ(Hard)
题目描述
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个可能存在 重复 元素值的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
输入输出样例
输入:nums = [1,3,5]
输出:1
题解
力扣官方
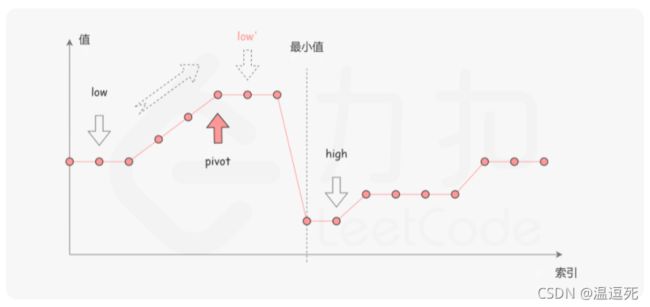
重复数组经过旋转后,可以得到下面折线图

在二分查找的每一步中,左边界为 left,右边界为 right,区间的中点为 mid,最小值就在该区间内。我们将中间元素 nums[mid] 与右边界元素 nums[high] 进行比较,可能会有以下的三种情况:
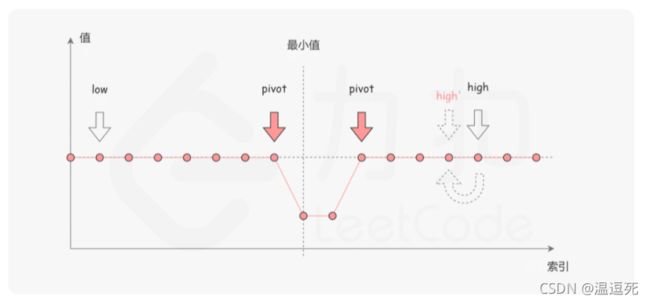
第一种情况:nums[mid] 最后,如果nums[mid]==nums[right],如下图,我们可以通过right–来判断 代码 题目描述 给定一个只包含整数的有序数组,每个元素都会出现两次,唯有一个数只会出现一次,找出这个数。 输入输出样例 题解 该题用二分法来做,主要是通过判断奇偶性进而来划分区间,其实如果该题并非排序,而且两个相同数字是靠在一起的,也可以通过二分法来做 主要分为4种情况 1.中间元素的同一元素在右边,且被 mid 分成两半的数组为偶数。 2.中间元素的同一元素在右边,且被 mid 分成两半的数组为奇数。 3.中间元素的同一元素在左边,且被 mid 分成两半的数组为偶数。 4.中间元素的同一元素在左边,且被 mid 分成两半的数组为奇数。 题目描述 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 输入输出样例 题解 先参考一波官方题解 代码 在进行刷题时,对于一些数组,特别是已经排序好的数组,可以优先考虑是否可以使用二分查找来进行解答。 二分查找,算法本身并不难理解,但是其边界以及各种题目变化比较多,比较难掌握,这是我个人做题时遇到的困难。关于二分查找区间问题,我也不知所措,这里提供我在其他博客上看到的两个小诀窍:首先是尝试熟练使用一种写法,比如左闭右开(满足 C++、Python 等语言的习惯)或左闭右闭(便于处理边界条件),尽量只保持这一种写法;第二是在刷题时思考如果最后区间只剩下一个数或者两个数,自己的写法是否会陷入死循环,如果某种写法无法跳出死循环,则考虑尝试另一种写法。
第二种情况:nums[mid]>nums[right],如下图,这说明最小值在nums[mid]的右侧,因此我们舍弃二分查找的左半部分。class Solution {
public:
int findMin(vector<int>& nums) {
int left=0,right=nums.size()-1,mid=0;
while(left<right){
mid=left+(right-left)/2;
if(nums[right]==nums[mid]){ //第三种情况
right--;
}
else if(nums[right]<nums[mid]){ //第二种情况
left=mid+1;
}else{ //第一种情况
right=mid;
}
}
return nums[left];
}
};
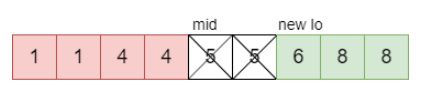
540.有序数组中的单一元素(Medium)
输入: nums = [1,1,2,3,3,4,4,8,8]
输出: 2
class Solution {
public:
int singleNonDuplicate(vector<int>& nums) {
int left=0,right=nums.size()-1,mid=0;
while(left<right){
mid=left+(right-left)/2;
bool flag=(right-mid)%2==0;
if(nums[mid]==nums[mid+1]){
if(flag){
left=mid+2;
}else{
right=mid-1;
}
}
else if(nums[mid]==nums[mid-1]){
if(flag){
right=mid-2;
}else{
left=mid+1;
}
}else{
return nums[mid];
}
}
return nums[left];
}
};
4.寻找两个正序数组的中位数(Hard)
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
class Solution {
public:
int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
/* 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
* 这里的 "/" 表示整除
* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
* 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
* 这样 pivot 本身最大也只能是第 k-1 小的元素
* 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组
* 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组
* 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数
*/
int m = nums1.size();
int n = nums2.size();
int index1 = 0, index2 = 0;
while (true) {
// 边界情况
if (index1 == m) {
return nums2[index2 + k - 1];
}
if (index2 == n) {
return nums1[index1 + k - 1];
}
if (k == 1) {
return min(nums1[index1], nums2[index2]);
}
// 正常情况
int newIndex1 = min(index1 + k / 2 - 1, m - 1);
int newIndex2 = min(index2 + k / 2 - 1, n - 1);
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
if (pivot1 <= pivot2) {
k -= newIndex1 - index1 + 1;
index1 = newIndex1 + 1;
}
else {
k -= newIndex2 - index2 + 1;
index2 = newIndex2 + 1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int totalLength = nums1.size() + nums2.size();
if (totalLength % 2 == 1) {
return getKthElement(nums1, nums2, (totalLength + 1) / 2);
}
else {
return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
}
}
};
总结