数据结构与算法【队列】的Java实现
目录
队列
基于单向循环链表实现
基于循环数组实现
双端队列
基于双向循环链表实现
基于数组实现
优先级队列
无序数组实现
有序数组的实现
基于堆的实现
队列
队列:以顺序的方式维护的一组数据集合,在一端添加数据,从另一端移除数据。习惯来说,添加的一端称为尾,移除的一端称为头。
通用接口
public interface Queue {
/**
* 插入队列
*/
boolean offer(E value);
/**
* 从队列中获取值并移除
*/
E poll();
/**
* 从队列中获取值但不移除
*/
E peek();
/**
* 检查队列是否已满
*/
boolean isFull();
/**
* 检查队列是否不为空
*/
boolean isEmpty();
} 基于单向循环链表实现
public class LinkedQueue implements Queue, Iterable {
//提供哨兵节点
private Node sentinel = new Node(null, null);
//提供尾节点
private Node tail = sentinel;
//队列大小
private int size = 0;
//队列容量
private int capacity = Integer.MAX_VALUE;
public LinkedQueue(int capacity) {
this.capacity = capacity;
tail.next = sentinel;
}
private static class Node {
Node next;
E value;
public Node(Node next, E value) {
this.next = next;
this.value = value;
}
}
@Override
public boolean offer(E value) {
//在队尾插入元素,选择尾插法
if (isFull()) {
return false;
}
Node node = new Node<>(sentinel, value);
tail.next = node;
tail = node;
size++;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
Node first = sentinel.next;
if (first==tail){
//如果是最后一个节点,那么将tail指向sentinel
tail =sentinel;
}
sentinel.next = first.next;
E value = first.value;
size--;
return value;
}
@Override
public E peek() {
return sentinel.next.value;
}
@Override
public boolean isFull() {
return size == capacity;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public Iterator iterator() {
return new Iterator() {
Node p = sentinel.next;
@Override
public boolean hasNext() {
return p != sentinel;
}
@Override
public E next() {
E value = p.value;
p = p.next;
return value;
}
};
}
} 基于循环数组实现
实现前,介绍一下环形数组与数组的区别
- 对比普通数组,起点和终点更为自由,不用考虑数据移动(普通数组移除元素时需要移动其他元素)
- “环”意味着不会存在【越界】问题
- 数组性能更佳
- 环形数组比较适合实现有界队列、RingBuffer 等
public class ArraysQueue implements Queue, Iterable {
private int head = 0;
private int tail = 0;
//用来记录循环数组大小
private final int length;
private E[] array;
@SuppressWarnings("all")
public ArraysQueue(int capacity) {
this.length = capacity + 1;
//加一是为尾指针留一个空间去判断是否队列已满
this.array = (E[]) new Object[length];
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
array[tail++] = value;
tail = tail % length;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
E value = array[head];
head = (head + 1) % length;
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return array[head];
}
@Override
public boolean isFull() {
if ((tail + 1) % length == head) {
return true;
}
return false;
}
@Override
public boolean isEmpty() {
return head == tail;
}
@Override
public Iterator iterator() {
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p != tail;
}
@Override
public E next() {
E value = array[p];
p = (p + 1) % length;
return value;
}
};
}
} 在Java源码中的基于数组实现的队列对容量有一个要求,即一定是2的n次方。之所以这么要求,是因为方便头指针和尾指针的边界确认。
我们的实现方式中指针的值是通过+1并取余来确定指针的下一个位置,也就是说,head和tail的值始终是在数组长度中。而在Java源码中,并没有规定head与tail的取值一定是数组长度内,而是不停的+1然后通过对数组长度的取余,来确定head与tail的下标位置。
但是这样又存在一个问题。那就是head或是tail超过了int类型所能表达的最大值后,再去取余会得到负数,使用负数去数组中拿元素会报错。为了解决这个问题,Java针对二进制特点采用了更高效率的实现方案。
就是规定数组长度一定是2的n次方
看下面例子
因此我们不需要在意符号位是否为负数,只需要关心余数的二进制即可。
对于如何通过二进制的方式获取到余数。是二进制的另一个特性
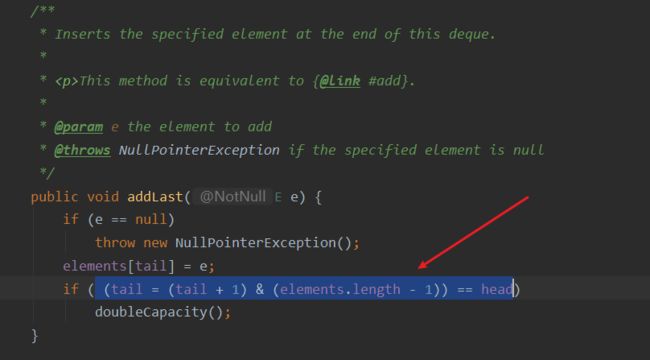
我们查看ArrayDeque源码中的添加元素方法
正是采用了二进制的位运算特性来控制head与tail在数组中的下标位置。如果用户指定数组队列不是一个2的n次方时,他会强制扩容到最近的2的n次方大小。具体实现方式如下
双端队列
与队列的区别就是两端都可以进行添加和删除。
Java 中 LinkedList 即为典型双端队列实现,不过它同时实现了 Queue 接口,也提供了栈的 push pop 等方法
简单接口定义
public interface Deque {
/**
* 队头插入
*/
boolean offerFirst(E value);
/**
* 队尾插入
*/
boolean offerLast(E value);
/**
* 队头出队
*/
E pollFirst();
/**
* 队尾出队
*/
E pollLast();
/**
* 获取队头元素
*/
E peekFirst();
/**
* 获取队尾元素
*/
E peekLast();
boolean isEmpty();
boolean isFull();
} 基于双向循环链表实现
public class LinkedListDeque implements Deque, Iterable {
private Node sentinel;
private int size = 0;
private int capacity = 8;
public LinkedListDeque(int capacity) {
this.capacity = capacity;
sentinel = new Node(null, null, null);
sentinel.prev = sentinel;
sentinel.next = sentinel;
}
static class Node {
Node prev;
E value;
Node next;
public Node(Node prev, E value, Node next) {
this.prev = prev;
this.value = value;
this.next = next;
}
}
@Override
public boolean offerFirst(E value) {
if (isFull()) {
return false;
}
Node offer = new Node<>(sentinel, value, sentinel.next);
//将哨兵节点的下一个节点的前驱节点设置为offer
sentinel.next.prev = offer;
//将哨兵节点的后驱节点设置为offer
sentinel.next = offer;
size++;
return true;
}
@Override
public boolean offerLast(E value) {
if (isFull()){
return false;
}
Node offer = new Node<>(sentinel.prev, value, sentinel);
//将哨兵节点的前驱节点的下一个节点设置为offer
sentinel.prev.next =offer;
//将哨兵节点的前驱节点设置为offer
sentinel.prev = offer;
size++;
return true;
}
@Override
public E pollFirst() {
if (isEmpty()){
return null;
}
Node pollNode = sentinel.next;
sentinel.next = pollNode.next;
pollNode.next.prev = sentinel;
size--;
return pollNode.value;
}
@Override
public E pollLast() {
if (isEmpty()){
return null;
}
Node pollNode = sentinel.prev;
pollNode.prev.next = sentinel;
sentinel.prev = pollNode.prev;
size--;
return pollNode.value;
}
@Override
public E peekFirst() {
return sentinel.next.value;
}
@Override
public E peekLast() {
return sentinel.prev.value;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == capacity;
}
@Override
public Iterator iterator() {
return new Iterator() {
Node p = sentinel.next;
@Override
public boolean hasNext() {
return p != sentinel;
}
@Override
public E next() {
E value = p.value;
p = p.next;
return value;
}
};
}
} 基于数组实现
public class ArrayDeque implements Deque, Iterable {
private int head = 0;
private int tail = 0;
private E[] array;
public ArrayDeque(int capacity) {
array = (E[]) new Object[capacity + 1];
}
@Override
public boolean offerFirst(E value) {
if (isFull()) {
return false;
}
head = dec(head, array.length);
array[head] = value;
return true;
}
@Override
public boolean offerLast(E value) {
if (isFull()) {
return false;
}
array[tail] = value;
tail = inc(tail, array.length);
return true;
}
@Override
public E pollFirst() {
if (isEmpty()){
return null;
}
E value = array[head];
head = inc(head,array.length);
return value;
}
@Override
public E pollLast() {
if (isEmpty()){
return null;
}
tail = dec(tail,array.length);
E value = array[tail];
return value;
}
@Override
public E peekFirst() {
return array[head];
}
@Override
public E peekLast() {
return array[dec(tail,array.length)];
}
@Override
public boolean isEmpty() {
return tail == head;
}
@Override
public boolean isFull() {
return (tail + 1) % array.length == head;
}
@Override
public Iterator iterator() {
return new Iterator() {
int p = head;
@Override
public boolean hasNext() {
return p != tail;
}
@Override
public E next() {
E e = array[p];
p = inc(p, array.length);
return e;
}
};
}
//加1工具方法。
static int inc(int i, int length) {
if (i + 1 >= length) {
return 0;
}
return i + 1;
}
//减1工具方法。
static int dec(int i, int length) {
if (i - 1 < 0) {
//返回数组最后一个下标位置
return length - 1;
}
return i - 1;
}
} 需要注意的是,为了节省内存空间,对于引用类型我们需要在poll时,对其进行置空操作,取消对引用类型的引用,便于GC回收。
优先级队列
虽然也是一端进一端出,但是与普通队列的区别在于,优先级高的先出队,可以不按顺序出队。要实现这个一共有三种实现方式。
无序数组实现
优先级接口,实体类需要实现该接口
public interface Priority {
int priority();
}实体类,除了存储值之外,还需要存储优先级
public class Entry implements Priority {
private int value;
private int priority;
public Entry(int value, int priority) {
this.value = value;
this.priority = priority;
}
@Override
public int priority() {
return priority;
}
@Override
public String toString() {
return "Entry{" +
"value=" + value +
", priority=" + priority +
'}';
}
}实现
public class PriorityQueue implements Queue {
private int size = 0;
//因为E继承了Priority因此,可以直接使用Priority
private Priority[] array;
public PriorityQueue(int capacity) {
array = new Priority[capacity];
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
array[size++] = value;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
int maxIndex = selectMax();
E value = (E) array[maxIndex];
remove(maxIndex);
return value;
}
private void remove(int maxIndex) {
System.arraycopy(array, maxIndex + 1, array, maxIndex, size - 1 - maxIndex);
array[--size] = null;//help GC
}
private int selectMax() {
int m = 0;
for (int i = 0; i < size; i++) {
if (array[i].priority() > array[m].priority()) {
m = i;
}
}
return m;
}
@Override
public E peek() {
if (isEmpty()){
return null;
}
int max = selectMax();
return (E) array[max];
}
@Override
public boolean isFull() {
return size == array.length;
}
@Override
public boolean isEmpty() {
return size == 0;
}
} 这种实现方式是在取出元素时进行一次selectMax(),得到优先级最高的元素下标。
有序数组的实现
public class PriorityQueue2 implements Queue {
private int size = 0;
private Priority[] array;
public PriorityQueue2(int capacity) {
array = new Priority[capacity];
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
//排序后插入
insert(value);
size++;
return true;
}
private void insert(E value) {
int i = size - 1;
while (i >= 0 && array[i].priority() > value.priority()) {
array[i + 1] = array[i];
i--;
}
array[i+1]=value;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
E value = (E) array[--size];
return value;
}
@Override
public E peek() {
if (isEmpty()) {
return null;
}
return (E) array[size-1];
}
@Override
public boolean isFull() {
return size == array.length;
}
@Override
public boolean isEmpty() {
return size == 0;
}
} 实现方式大体和无序数组的实现方式相同,不过是在插入元素时,对插入元素的优先级在数组中进行一个排序,得到插入的下标。
基于堆的实现
堆是一种基于树的数据结构,通常用完全二叉树实现。堆的特性如下
- 在大顶堆中,任意节点 C 与它的父节点 P 符合 P.value ≥ C.value
- 而小顶堆中,任意节点 C 与它的父节点 P 符合 P.value ≤ C.value
- 最顶层的节点(没有父亲)称之为 root 根节点
完全二叉树的特点是,除了最后一层,每一层的都是填满的,最后一层从左向右开始填充。
完全二叉树可以使用数组进行表示
特征
- 如果从索引 0 开始存储节点数据
- 节点 i 的父节点为 floor((i-1)/2),当 i>0 时
- 节点 i 的左子节点为 2i+1,右子节点为 2i+2,当然它们得 < size
- 如果从索引 1 开始存储节点数据
- 节点 i 的父节点为 floor(i/2),当 i > 1 时
- 节点 i 的左子节点为 2i,右子节点为 2i+1,同样得 < size
public class PriorityQueue3 implements Queue {
private int size = 0;
private Priority[] array;
public PriorityQueue3(int capacity) {
array = new Priority[capacity];
}
@Override
public boolean offer(E value) {
if (isFull()) {
return false;
}
//获取需要插入的下标
int child = size++;
//获取父结点下标
int parent = (child - 1) / 2;
while (child > 0 && array[parent].priority() < value.priority()) {
array[child] = array[parent];
child = parent;
parent = (child - 1) / 2;
}
array[child] = value;
return true;
}
@Override
public E poll() {
if (isEmpty()) {
return null;
}
E value = (E) array[0];
//将最后一个节点放在root位置上
array[0] = array[--size];
array[size] = null;
//找到新的root节点应该存放的位置
shiftDown(0);
return value;
}
private void shiftDown(int parent) {
//获取新的root节点的左右子节点下标
int leftChild = parent * 2 + 1;
int rightChild = leftChild + 1;
//取左右节点较大的值
int max = parent;
//如果左边节点优先级更大
if (leftChild < size && array[leftChild].priority() > array[max].priority()) {
max = leftChild;
} else if (rightChild < size && array[rightChild].priority() > array[max].priority()) {
max = rightChild;
}
if (max != parent){
swap(parent,max);
shiftDown(max);
}
//说明此时已经是符合大顶堆的特点了
}
private void swap(int parent, int max) {
Priority temp = array[parent];
array[parent] = array[max];
array[max] = temp;
}
@Override
public E peek() {
return (E) array[0];
}
@Override
public boolean isFull() {
return size == array.length;
}
@Override
public boolean isEmpty() {
return size == 0;
}
}