pytorch深度学习基础（五）——SoftMax函数反向传递公式推导及代码实现

SoftMax函数介绍

简介

softmax函数是常用的输出层函数，常用来解决互斥标签的多分类问题。当然由于他是非线性函数，也可以作为隐藏层函数使用

公式

假设我们有若干输入[x1, x2, x3…xn]，对应的输出为[y1, y2, y3…yn]，对于SoftMax函数我们有
$$y_i=\frac{e^{x_i}}{{\sum }_{k=0}{e}^{{}^{x_k}}}$$

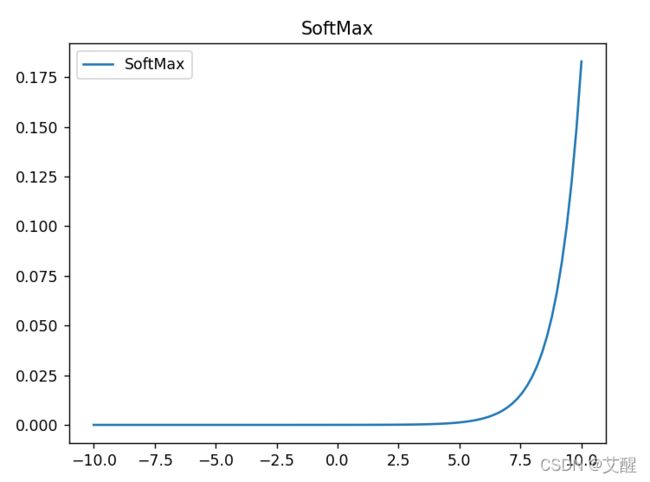
图像

反向传递公式推导

SoftMax函数比较特殊，他有多个输入和输出，并且每个输出与所有的输入都有关，所以这个函数输出对于多个输入都有一个偏导数，也就是SoftMax可以得到多个偏导数。对于SoftMax我们有两种情况

当输入坐标与输出坐标相对应时

$$\frac{\partial y_i}{\partial x_j}=\frac{\partial y_i}{\partial x_i}$$
$$=\frac{e^{x_i}\cdot ({\sum }_{k，i=j}{e}^{x_i})-e^{x_i}\cdot e^{x_i}}{({\sum }_{k,i=j}{e}^{x_k}{)}^2}$$
$$=\frac{e^{x_i}}{{\sum }_{k,i=j}{e}^{x_k}}-(\frac{e^{x_i}}{{\sum }_{k,i=j}{e}^{x_k}}{)}^2$$
$$=y_i(1-y_i)$$

当输入坐标与输出坐标不对应时

$$\frac{\partial y_i}{\partial x_j}=-\frac{e^{x_i}\cdot e^{x_j}}{({\sum }_k{e}^{x_k}{)}^2}$$
$$=-\frac{e^{x_i}}{{\sum }_{k,i!=j}{e}^{x_k}}\cdot \frac{e^{x_j}}{{\sum }_{k,i!=j}{e}^{x_k}}=-y_i\cdot y_j$$

两种情况合并

$$\begin{gathered} \frac{\partial y_i}{\partial x_j}=\frac{e^{x_i}}{{\sum }_{k,i=j}{e}^{x_k}}-(\frac{e^{x_i}}{{\sum }_{k,i=j}{e}^{x_k}}{)}^2-\frac{e^{x_i}}{{\sum }_{k,i!=j}{e}^{x_k}}\cdot \frac{e^{x_j}}{{\sum }_{k,i!=j}{e}^{x_i}} \\ =\frac{e^{x_i}}{{\sum }_{k,i=j}{e}^{x_k}}-\frac{e^{x_i}\cdot e^{x_j}}{({\sum }_k{e}^{x_k}{)}^2}=y_i-y_i\cdot y_j \end{gathered}$$
按照正常的推导到这里就应该结束了，但我们为了代码实现方便，可以将i和j近似的看成相同的，这样我们就可以得到一个效果类似的不太严谨的代码
$$\frac{\partial y}{\partial x}=y\cdot (1-y)$$

代码实现

一个简单但不严谨的实现

class SoftMax():
    def __init__(self):
        pass
    def _softmax(self,x):
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T
    
    def forward(self,input):
        return self._softmax(input)
    
    def backward(self, input, grad_output):
        out = self.forward(input)
        return grad_output * out * (1 - out)

正规代码

代码

class SoftMax():
    def __init__(self):
        pass
    def _softmax(self,x):
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T
    
    def forward(self,input):
        return self._softmax(input)
    
    def backward(self, input, grad_output):
        out = self.forward(input)
        ret = []
        for i in range(grad_output.shape[0]):
        	softmax_grad = np.diag(out[i]) - np.outer(out[i], out[i])
        	ret.append(np.dot(softmax_grad, grad_output[i].T))
        ret = np.array(ret)
        return ret

解析
这里的实现可能较为难以理解，我们使用IDLE在下面进行步骤分解解释

先假设out

>>> import numpy as np
>>> out = np.array([[1, 2, 3], [4, 5, 6]])
>>> out
array([[1, 2, 3],
       [4, 5, 6]])
       

grad_output的形状与out相识，我们假设

>>> grad_output = np.array([[3, 4, 5], [6, 7, 8]])
>>> grad_output
array([[3, 4, 5],
       [6, 7, 8]])
       

我们回顾上面推导的反向传递的公式为
$$\frac{\partial y_i}{\partial x_j}=y_i-y_i\cdot y_j$$
yi即为第i位为每i行对应的值，可以使用np.diag实现

我们取第0位来测试

>>> out[0]
array([1, 2, 3])

>>> np.diag(out[0])
array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])

$$y_i\cdot y_j即为i行j列设置为y_i和y_j的乘积$$

>>> np.outer(out[0], out[0])
array([[1, 2, 3],
       [2, 4, 6],
       [3, 6, 9]])

所以softmax的梯度为

>>> softmax_grad = np.diag(out[0]) - np.outer(out[0], out[0])
>>> softmax_grad
array([[ 0, -2, -3],
       [-2, -2, -6],
       [-3, -6, -6]])

那么向前传递的值应该为softmax的梯度和后边传过来的梯度grad_output，我们仍然以第0位为例，这样我们就可以得到第0位的梯度，那么后续我们遍历各个位获得梯度即可。

>>> softmax_grad.dot(grad_output[0].T)
array([-23, -44, -63])