bp网络损失函数及梯度推导理解
跟随吴恩达老师的机器学习课程学习了一段时间,把最近较难的bp网络的一些推导梳理一下。
一、损失函数
logistic回归
假设只有一个输入样本,则代价函数是:
J ( θ ) = − y l o g h ( x ) − ( 1 − y ) l o g ( 1 − h ) J(\theta)=-ylogh(x)-(1-y)log(1-h) J(θ)=−ylogh(x)−(1−y)log(1−h)
多个输入样本只要累加就可以:
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J(θ)=−\frac1m[\sum_{i=1}^{m}y^{(i)}logh_θ(x^{(i)})+(1−y^{(i)})log(1−h_θ(x^{(i)}))] J(θ)=−m1[i=1∑my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
这里的损失函数推导可以参考这篇文章Logistic回归代价函数的数学推导及实现
Neural Network
对于多层神经网络对应的对应损失函数为:
J ( θ ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) l o g h θ ( x ( i ) ) k + ( 1 − y k ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) k ] J(θ)=−\frac1m [ \sum_{i=1}^{m} \sum_{k=1}^{K} y_k^{(i)} logh_θ(x^{(i)})_k + (1−y_k^{(i)}) log(1−h_θ(x^{(i)}))_k] J(θ)=−m1[i=1∑mk=1∑Kyk(i)loghθ(x(i))k+(1−yk(i))log(1−hθ(x(i)))k]
这里的大K对应最后网络的输出,当处理二分类时可以直接用一个单元来输出(用0 1来表示结果)
当处理三分类时,网络最后的输出为三个节点,此时输出及数据集标签应当为一个1*3的矩阵
y = [ 1 0 0 ] y=\begin{bmatrix} 1 \\ 0 \\ 0\end{bmatrix} y=⎣⎡100⎦⎤
y k y_k yk代表y中第k个数 所以对比logistic的损失函数,这里只是最后将y中每一行当作输出再累加
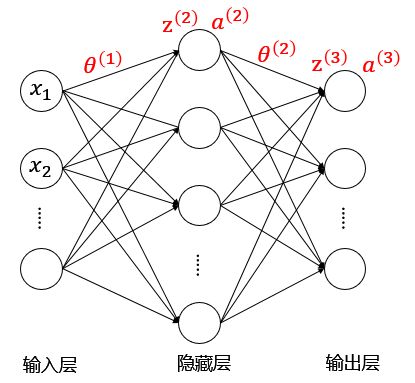
二、神经网络正向传播
- θ ( i ) θ^{(i)} θ(i)代表第 i i i层的参数矩阵
- z ( l ) z^{(l)} z(l)代表第 i i i层的输入
- a ( l ) a^{(l)} a(l)代表第 i i i层的输出
传递过程:
- a ( 1 ) = x a^{(1)}=x a(1)=x
- z ( 2 ) = θ ( 1 ) a ( 1 ) z^{(2)}=θ^{(1)}a^{(1)} z(2)=θ(1)a(1)
- a ( 2 ) = g ( z ( 2 ) ) ( a d d a 0 ( 2 ) ) a^{(2)}=g(z^{(2)})(add \ a_0^{(2)}) a(2)=g(z(2))(add a0(2))
- z ( 3 ) = θ ( 2 ) a ( 2 ) z^{(3)}=θ^{(2)}a^{(2)} z(3)=θ(2)a(2)
- h = a ( 3 ) = g ( z ( 3 ) ) h=a^{(3)}=g(z^{(3)}) h=a(3)=g(z(3))
其中 g g g为sigmoid激活函数。
三、神经网络的反向传递
现在我们可以从前往后得到整个网络的损失函数 J ( θ ) J(θ) J(θ)
下一步就是用损失函数对我们所给出的参数求偏导得到梯度即 ∂ J ( θ ) ∂ θ ( 2 ) \bf\frac{\partial J(θ)}{\partial θ^{(2)}} ∂θ(2)∂J(θ) ∂ J ( θ ) ∂ θ ( 1 ) \bf\frac{\partial J(θ)}{\partial θ^{(1)}} ∂θ(1)∂J(θ)
这里用到链式求导法则 ∂ J ( θ ) ∂ θ ( 2 ) = ∂ J ( θ ) ∂ a ( 3 ) ∂ a ( 3 ) ∂ z ( 3 ) ∂ z ( 3 ) ∂ θ ( 2 ) \bf \frac{\partial J(θ)}{\partial θ^{(2)}}= \bf\frac{\partial J(θ)}{\partial a^{(3)}} \bf\frac{\partial a^{(3)}}{\partial z^{(3)}} \bf \frac{\partial z^{(3)}}{\partial θ^{(2)}} ∂θ(2)∂J(θ)=∂a(3)∂J(θ)∂z(3)∂a(3)∂θ(2)∂z(3)
-
损失函数 J ( θ ) J(θ) J(θ)
J ( θ ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) l o g h θ ( x ( i ) ) k + ( 1 − y k ( i ) ) l o g ( 1 − h θ ( x ( i ) ) k ) ] = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) l o g ( a k ( 3 ) ) + ( 1 − y k ( i ) ) l o g ( 1 − a k ( 3 ) ) ] J(θ)=−\frac1m [ \sum_{i=1}^{m} \sum_{k=1}^{K} y_k^{(i)} log\ h_θ(x^{(i)})_k + (1−y_k^{(i)}) log(1− h_θ(x^{(i)})_k)]\\ =−\frac1m [ \sum_{i=1}^{m} \sum_{k=1}^{K} y_k^{(i)} log(a_k^{(3)}) + (1−y_k^{(i)}) log(1−a_k^{(3)})] J(θ)=−m1[i=1∑mk=1∑Kyk(i)log hθ(x(i))k+(1−yk(i))log(1−hθ(x(i))k)]=−m1[i=1∑mk=1∑Kyk(i)log(ak(3))+(1−yk(i))log(1−ak(3))] -
∂ J ( θ ) ∂ a ( 3 ) \bf\frac{\partial J(θ)}{\partial a^{(3)}} ∂a(3)∂J(θ)
∂ J ( θ ) ∂ a ( 3 ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) 1 a k ( 3 ) + ( 1 − y k ( i ) ) − 1 1 − a k ( 3 ) ] = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) − a k ( 3 ) a k ( 3 ) ( 1 − a k ( 3 ) ) ] ( 通 分 即 可 ) \frac{\partial J(θ)}{\partial a^{(3)}} = −\frac1m [ \sum_{i=1}^{m} \sum_{k=1}^{K} y_k^{(i)} \frac{1}{a_k^{(3)}} + (1−y_k^{(i)}) \frac{-1}{1−a_k^{(3)}}]\\[2ex] =−\frac1m [ \sum_{i=1}^{m} \sum_{k=1}^{K} \frac{y_k^{(i)} -a_k^{(3)}} {a_k^{(3)} (1-a_k^{(3)})}] (通分即可) ∂a(3)∂J(θ)=−m1[i=1∑mk=1∑Kyk(i)ak(3)1+(1−yk(i))1−ak(3)−1]=−m1[i=1∑mk=1∑Kak(3)(1−ak(3))yk(i)−ak(3)](通分即可) -
∂ a ( 3 ) ∂ z ( 3 ) \bf\frac{\partial a^{(3)}}{\partial z^{(3)}} ∂z(3)∂a(3)
a ( 3 ) = g ( z ( 3 ) ) ∂ a ( 3 ) ∂ z ( 3 ) = a ( 3 ) ( 1 − a ( 3 ) ) a^{(3)}=g(z^{(3)})\\[2ex] \frac{\partial a^{(3)}}{\partial z^{(3)}} = a^{(3)} (1-a^{(3)}) a(3)=g(z(3))∂z(3)∂a(3)=a(3)(1−a(3))
这里涉及到sigmoid函数求导:
s i g m o i d 函 数 : f ( x ) = 1 1 + e ( − x ) f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) ( 可 以 自 己 求 一 下 导 ) sigmoid函数:f(x)=\frac1{1+{\rm e}^{(-x)}}\\[1ex] f^\prime(x)=f(x)(1-f(x))\\[1ex] (可以自己求一下导) sigmoid函数:f(x)=1+e(−x)1f′(x)=f(x)(1−f(x))(可以自己求一下导) -
∂ z ( 3 ) ∂ θ ( 2 ) \bf\frac{\partial z^{(3)}}{\partial \theta^{(2)}} ∂θ(2)∂z(3)
z ( 3 ) = θ ( 2 ) a ( 2 ) ∂ z ( 3 ) ∂ θ ( 2 ) = a ( 2 ) z^{(3)}=θ^{(2)}a^{(2)}\\[2ex] \frac{\partial z^{(3)}}{\partial \theta^{(2)}}=a^{(2)} z(3)=θ(2)a(2)∂θ(2)∂z(3)=a(2)
最后我们可以得到最终的偏导:
∂ J ( θ ) ∂ θ ( 2 ) = ∂ J ( θ ) ∂ a ( 3 ) ∂ a ( 3 ) ∂ z ( 3 ) ∂ z ( 3 ) ∂ θ ( 2 ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) − a k ( 3 ) a k ( 3 ) ( 1 − a k ( 3 ) ) ] a ( 3 ) ( 1 − a ( 3 ) ) a ( 2 ) = − 1 m [ ∑ i = 1 m ∑ k = 1 K y k ( i ) − a k ( 3 ) ] a ( 2 ) \frac{\partial J(θ)}{\partial θ^{(2)}}= \frac{\partial J(θ)}{\partial a^{(3)}} \frac{\partial a^{(3)}}{\partial z^{(3)}} \frac{\partial z^{(3)}}{\partial θ^{(2)}}\\[2ex] \ \ \ \ \ =−\frac1m [ \sum_{i=1}^{m} \sum_{k=1}^{K} \frac{y_k^{(i)} -a_k^{(3)}} {a_k^{(3)} (1-a_k^{(3)})}] \ {a^{(3)} (1-a^{(3)})} \ a^{(2)}\\[2ex] =−\frac1m [ \sum_{i=1}^{m} \sum_{k=1}^{K} {y_k^{(i)} -a_k^{(3)}} ] \ a^{(2)} ∂θ(2)∂J(θ)=∂a(3)∂J(θ)∂z(3)∂a(3)∂θ(2)∂z(3) =−m1[i=1∑mk=1∑Kak(3)(1−ak(3))yk(i)−ak(3)] a(3)(1−a(3)) a(2)=−m1[i=1∑mk=1∑Kyk(i)−ak(3)] a(2)
我们定义第三层误差值(此处并非真正意义上的误差) δ ( 3 ) = a ( 3 ) − y \delta^{(3)}=a^{(3)}-y δ(3)=a(3)−y
进一步得到:
∂ J ( θ ) ∂ θ ( 2 ) = 1 m δ ( 3 ) a ( 2 ) ( 这 里 做 向 量 化 处 理 省 去 之 前 的 累 加 和 ) \frac{\partial J(θ)}{\partial θ^{(2)}}=\frac1m \ \delta^{(3)} a^{(2)} \\[1ex] (这里做向量化处理省去之前的累加和) ∂θ(2)∂J(θ)=m1 δ(3)a(2)(这里做向量化处理省去之前的累加和)
用同样的方法去计算 ∂ J ( θ ) ∂ θ ( 1 ) \bf\frac{\partial J(θ)}{\partial θ^{(1)}} ∂θ(1)∂J(θ),可以得到:
∂ J ( θ ) ∂ θ ( 1 ) = ∂ J ( θ ) ∂ a ( 3 ) ∂ a ( 3 ) ∂ z ( 3 ) ∂ z ( 3 ) ∂ a ( 2 ) ∂ a ( 2 ) ∂ z ( 2 ) ∂ z ( 2 ) ∂ θ ( 1 ) = 1 m δ ( 3 ) θ ( 2 ) g ′ ( z ( 2 ) ) a ( 1 ) \frac{\partial J(θ)}{\partial θ^{(1)}}=\frac{\partial J(θ)}{\partial a^{(3)}} \frac{\partial a^{(3)}}{\partial z^{(3)}} \frac{\partial z^{(3)}}{\partial a^{(2)}} \frac{\partial a^{(2)}}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial θ^{(1)}}\\[2ex] =\frac1m \ \delta^{(3)}\theta^{(2)}g^\prime(z^{(2)})a^{(1)} ∂θ(1)∂J(θ)=∂a(3)∂J(θ)∂z(3)∂a(3)∂a(2)∂z(3)∂z(2)∂a(2)∂θ(1)∂z(2)=m1 δ(3)θ(2)g′(z(2))a(1)
同样令
δ ( 2 ) = δ ( 3 ) θ ( 2 ) g ′ ( z ( 2 ) ) \delta^{(2)}=\delta^{(3)}\theta^{(2)}g^\prime(z^{(2)}) δ(2)=δ(3)θ(2)g′(z(2))
所以有:
∂ J ( θ ) ∂ θ ( 1 ) = 1 m δ ( 2 ) a ( 1 ) \frac{\partial J(θ)}{\partial θ^{(1)}}=\frac1m\ \delta^{(2)} a^{(1)} ∂θ(1)∂J(θ)=m1 δ(2)a(1)
最后将 ∂ J ( θ ) ∂ θ ( 2 ) \bf\frac{\partial J(θ)}{\partial θ^{(2)}} ∂θ(2)∂J(θ) ∂ J ( θ ) ∂ θ ( 1 ) \bf\frac{\partial J(θ)}{\partial θ^{(1)}} ∂θ(1)∂J(θ)相加即为总梯度,之后再用梯度下降或其他优化方法来求解出最佳参数,至此这个三层网络的反向推导就完成了。
四、总结
接着以四层网络为例作为总结,简洁展示整个梯度的计算
1、每一层的“误差”
- δ ( 4 ) = a ( 4 ) − y \delta^{(4)}=a^{(4)}-y δ(4)=a(4)−y
- δ ( 3 ) = δ ( 4 ) θ ( 3 ) g ′ ( z ( 3 ) ) \delta^{(3)}=\delta^{(4)}\theta^{(3)}g^\prime(z^{(3)}) δ(3)=δ(4)θ(3)g′(z(3))
- δ ( 2 ) = δ ( 3 ) θ ( 2 ) g ′ ( z ( 2 ) ) \delta^{(2)}=\delta^{(3)}\theta^{(2)}g^\prime(z^{(2)}) δ(2)=δ(3)θ(2)g′(z(2))
2、梯度
- Δ ( 3 ) = a ( 3 ) δ ( 4 ) \Delta^{(3)}=a^{(3)}\delta^{(4)} Δ(3)=a(3)δ(4)
- Δ ( 2 ) = a ( 2 ) δ ( 3 ) \Delta^{(2)}=a^{(2)}\delta^{(3)} Δ(2)=a(2)δ(3)
- Δ ( 1 ) = a ( 1 ) δ ( 2 ) \Delta^{(1)}=a^{(1)}\delta^{(2)} Δ(1)=a(1)δ(2)
3、总梯度
D = 1 m ( Δ ( 1 ) + Δ ( 2 ) + Δ ( 3 ) ) D=\frac1m \ (\Delta^{(1)}+\Delta^{(2)}+\Delta^{(3)}) D=m1 (Δ(1)+Δ(2)+Δ(3))