leetcode栈和队列三剑客

用队列实现栈

队列是先进先出的，而栈是只能在栈顶进行出栈和入栈，那我们这道题要用队列来实现栈的话，这里给的思路是两个队列，因为两个队列的话就可以相互导数据，比如我们来实现这个题目的push函数，我们的栈是只能在栈顶进行操作，那其实插入就也可以在队列的尾部进行插入，但是我们是两个队列，我们不能在空的队列进行插入，这样顺序就会乱，所以我们这里需要做的就是在不是空的队列进行插入操作。

那如果我们的栈要实现出栈该怎么做呢，我们先来看一下下面的这个图。

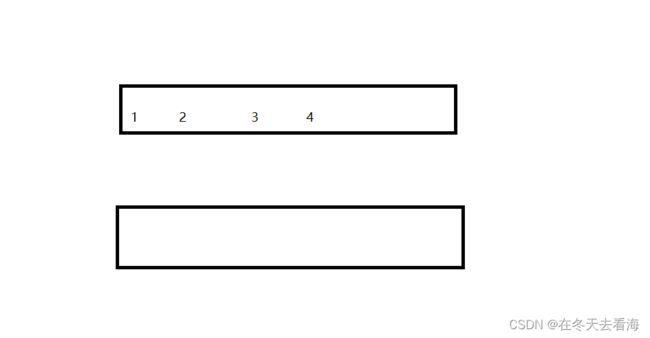
我们这里的出栈不是出第一个元素1，而是想办法把我们这里第一个队列的4出去，那因为队列只能在头上进行pop那我们这里可以先把第一个队列的前三个数据导入到第二个队列中，然会在pop第一个队列就可以了。代码实现就是下面这个图

我们的队列是始终保持一个是有数据的，一个是为空的，比如我们如果是取栈顶的元素，这里我们是确保取出不为空的队列数据的front，所以这个函数来实现也是特别的简单。

这道题的整个代码思路就是下面（我们这里用的是C语言，所以要自己实现一个队列）

#pragma once
#include
#include
#include
#include
typedef int QDataType;

typedef struct QListNode
{
	struct QListNode* next;
	QDataType data;
}QNode;

// 队列的结构 
typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Queue;

// 初始化队列 
void QueueInit(Queue* q);
// 队尾入队列 
void QueuePush(Queue* q, QDataType data);
// 队头出队列 
void QueuePop(Queue* q);
// 获取队列头部元素 
QDataType QueueFront(Queue* q);
// 获取队列队尾元素 
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数 
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
bool QueueEmpty(Queue* q);
// 销毁队列 
void QueueDestroy(Queue* q);







// 初始化队列 
void QueueInit(Queue* q)
{
	assert(q);
	q->head = q->tail = NULL;
	q->size = 0;


}
// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->next = NULL;
	newnode->data = data;
	if (q->head == NULL)
	{
		q->head = q->tail = newnode;

	}
	else
	{
		q->tail->next = newnode;
		q->tail = newnode;
	}
	q->size++;
}
// 队头出队列 
void QueuePop(Queue* q)
{
	assert(q);
	assert(q->size >= 0);
	assert(q->head != NULL);
	QNode* del = q->head;
	q->head = q->head->next;
	free(del);
	del = NULL;
	if (q->head == NULL)
		q->tail = NULL;
	q->size--;
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(q);
	assert(q->head);
	return q->head->data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(q);
	assert(q->head);
	return q->tail->data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);
	return q->size;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
bool QueueEmpty(Queue* q)
{
	assert(q);
	return q->head == NULL;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* cur = q->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	q->head = q->tail = NULL;
}

typedef struct {
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() {
    MyStack* q = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&q->q1);
    QueueInit(&q->q2);
    return q;
}

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1, x);
    }
    else
    {
        QueuePush(&obj->q2, x);
    }
}

int myStackPop(MyStack* obj) {
    Queue* empty = &obj->q1;
    Queue* nonempty = &obj->q2;
    if(QueueEmpty(nonempty))
    {
        empty = &obj->q2;
        nonempty = &obj->q1;
    }
    while(QueueSize(nonempty) > 1)
    {
        QueuePush(empty, QueueFront(nonempty));
        QueuePop(nonempty);
    }
    int ret = QueueFront(nonempty);
    QueuePop(nonempty);
    return ret;
}

int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) {
       return QueueEmpty(&obj->q1) &&  QueueEmpty(&obj->q2);

}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);

}

/**
 * Your MyStack struct will be instantiated and called as such:
 * MyStack* obj = myStackCreate();
 * myStackPush(obj, x);
 
 * int param_2 = myStackPop(obj);
 
 * int param_3 = myStackTop(obj);
 
 * bool param_4 = myStackEmpty(obj);
 
 * myStackFree(obj);
*/

用栈实现队列

有了前面的思路，我们知道栈的实现是要有两个队列才可以实现的，那同样我们如果要用栈实现队列的话，也得用两个栈来实现，这里我们的两个栈就有主要的区别，我们一个栈可以来当pop栈，还有一个栈可以当成push栈，这样的话，我们就有了分工的作用，后续在插入的时候我们只要在pop栈进行插入就可以了。

那我们先来实现一下我们该怎么初始化，初始化我们直接给两个栈

这里记住我们去初始化这俩个栈的时候我们是不知道该去怎么初始化，我们直接调用他们的函数就可以了，就不用去记住他们是怎么的一个样子。

那我们push就需要在push栈中push就可以了

这里的pop需要注意一些东西
如果popST为空，则将pushST的数据倒过来，就符合先进先出的顺序，如果不为空直接在栈顶进行pop就ok，但是我们这里如果一开始pop为空的，我们需要先把数据倒过来之后才可以进行下一部，我们前面就说过只有pop栈是pop的，push只是push，那我们就要进行判断，然会进行导数据这个操作。

下一个取出队列的元素，这个就很简单，就是复用上面的代码就可以，只是我们是取出来，不需要进行pop

那这道题就完成了，下面的就口函数我就直接给代码了（这里还是要自己实现一下栈）

#include 
#include 
#include 
#include 

静态实现（固定数组的长度）
//struct Stack
//{
//	int a[N];
//	int top; //栈顶的位置
//};


typedef int  STDataType;
//动态实现（固定数组的长度）
typedef struct Stack
{
	STDataType* a;   //传递数组地址，可以动态的进行扩容
	int top;   //栈顶的位置
	int capacity;   //容量
}ST;

//初始化
void StackInit(ST* ps);

//销毁
void StackDestory(ST* ps);

//压栈
void StackPush(ST* ps, STDataType x);

//出栈
void StackPop(ST* ps);

//判断栈是否为空
bool StackEmpty(ST* ps);

//计算栈的大小
int StackSize(ST* ps);

//初始化
void StackInit(ST* ps)
{
	assert(ps);

	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;  //初始化top为0，则相当于从栈顶的下一个位置开始，则先赋值，再进行++操作
}


//销毁
void StackDestory(ST* ps)
{
	assert(ps);

	free(ps->a);
	ps->a = NULL;

	ps->capacity = 0;
	ps->top = 0;
}

//压栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	
	//如果当前的空间不够就需要进行扩容
	if (ps->capacity == ps->top)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		ps->a = (STDataType*)realloc(ps->a, newCapacity * sizeof(STDataType));
		if (ps->a == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		//当前的空间等于新的空间的大小
		ps->capacity = newCapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
	

}

//出栈
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}

//判断栈是否为空
bool StackEmpty(ST* ps)
{
	assert(ps);

	return ps->top == 0;  //判断它的顶部是否为0

}

//计算栈的大小
int StackSize(ST* ps)
{
	assert(ps);

	return ps->top;   //返回栈顶就是元素的个数
}

//获取栈顶元素
STDataType StackTop(ST* ps)
{
	assert(ps);

	assert(ps->top > 0);

	return ps->a[ps->top - 1];   //top是栈顶的下一个元素，想找栈顶元素则进行减一的操作
}

//获取栈顶元素
STDataType StackTop(ST* ps);
typedef struct {
     ST pushST;
     ST popST;

} MyQueue;


MyQueue* myQueueCreate() {
   MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
   assert(obj);
   StackInit(&obj->pushST);
   StackInit(&obj->popST);

   return obj;
}

void myQueuePush(MyQueue* obj, int x) {
    assert(obj);
    StackPush(&obj->pushST,x);

}

int myQueuePop(MyQueue* obj) {
    assert(obj);
    //如果popST为空，则将pushST的数据倒过来，就符合先进先出的顺序
    if(StackEmpty(&obj->popST))
    {
        while(!StackEmpty(&obj->pushST))
        {
            StackPush(&obj->popST,StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }

    }
    int front =  StackTop(&obj->popST);
    StackPop(&obj->popST);

    return front;

}

int myQueuePeek(MyQueue* obj) {
    assert(obj);
    //如果popST为空，则将pushST的数据倒过来，就符合先进先出的顺序
    if(StackEmpty(&obj->popST))
    {
        while(!StackEmpty(&obj->pushST))
        {
            StackPush(&obj->popST,StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }

    }

    return  StackTop(&obj->popST);;

}

bool myQueueEmpty(MyQueue* obj) {
    assert(obj);
    return StackEmpty(&obj->pushST) && StackEmpty(&obj->popST);

}

void myQueueFree(MyQueue* obj) {
     assert(obj);
    StackDestory(&obj->pushST);
    StackDestory(&obj->popST);

    free(obj);

}
/**
 * Your MyQueue struct will be instantiated and called as such:
 * MyQueue* obj = myQueueCreate();
 * myQueuePush(obj, x);
 
 * int param_2 = myQueuePop(obj);
 
 * int param_3 = myQueuePeek(obj);
 
 * bool param_4 = myQueueEmpty(obj);
 
 * myQueueFree(obj);
*/

/**
 * Your MyQueue struct will be instantiated and called as such:
 * MyQueue* obj = myQueueCreate();
 * myQueuePush(obj, x);
 
 * int param_2 = myQueuePop(obj);
 
 * int param_3 = myQueuePeek(obj);
 
 * bool param_4 = myQueueEmpty(obj);
 
 * myQueueFree(obj);
*/

后面这个题比前面两道简单一点，是关于栈的。。

有效的括号

这个题我们用栈来实现，为什么用栈是因为这样时间复杂度就是O（N）我们只要遍历一遍就可以了，但是我们这个题目要知道考什么，一个我们必须数量进行匹配，另一个是顺序匹配，比如左括号（ 得和右）进行匹配，所以我们这里需要做的就是左括号这些入栈，然后右括号进行匹配，如果匹配成功的化原来里的括号要进行出栈，然会字符s往后继续++，但是如果有一个括号比右括号不是和我们的左括号匹配的话，我们需要进行的操作就是直接返回false就可以了，如果匹配成功的话出循环就是空栈，所以我们这里就可以直接返回true，但是还是有一个问题就是，在循环里面的时候，会出现越界访问

越界访问出现的情况就是有右括号，然后没有一个左括号在栈里面，我们这个取top的时候就可以直接返回。

下面是这个题的代码。

#include
#include
#include
#include

typedef char STDateType;
typedef struct Stack
{
	STDateType* a;
	int top;
	int capacity;
}ST;


void Init(ST* ps);

void Push(ST* ps, STDateType x);

void Pop(ST* ps);

STDateType Top(ST* ps);

void Dstory(ST* ps);

bool Empty(ST* ps);

int Size(ST* ps);


void Init(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = -1;
}

void Push(ST* ps, STDateType x)
{
	assert(ps);
	if (ps->top + 1 == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDateType* tmp =(STDateType*) realloc(ps->a, sizeof(STDateType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->capacity = newcapacity;
		ps->a = tmp;
	}
		ps->top++;

	ps->a[ps->top] = x;

}


void Pop(ST* ps)
{
	assert(ps);
	assert(ps->top >= 0);
	ps->top--;
}


void Dstory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->capacity = 0;
}

STDateType Top(ST* ps)
{
	assert(ps);
	assert(ps->top>=0);
	return ps->a[ps->top];
}


bool Empty(ST* ps)
{
	assert(ps);
	return ps->top == -1;
}




int Size(ST* ps)
{
	assert(ps);
	return ps->top + 1;
}

bool isValid(char* s) {
    ST st;
    Init(&st);
    while(*s)
    {
        if(*s == '(' || *s == '[' || *s == '{')
        {
            Push(&st, *s);
            s++;
        }
        else
        {
					if(Empty(&st))
					{
						return false;
					}
          char top = Top(&st);
					 Pop(&st);
					 if((*s == ')' && top != '(')|| (*s == ']' && top != '[')|| (*s == '}' && top != '{'))
            {
                return false;
            }
            s++;
        }
    }
    if(Empty(&st))
        return true;


    return false;
}

那今天三剑客就分享到这里，我们下次再见。