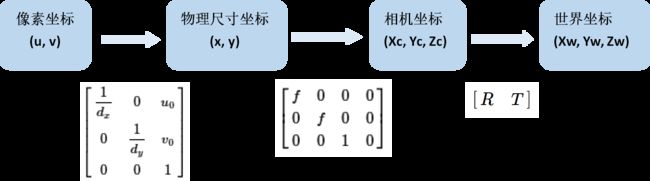
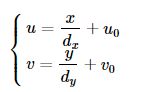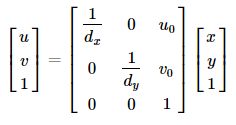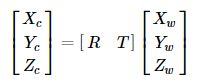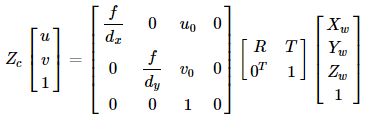【转】机器视觉 之 三个坐标系转换

转自：https://www.cnblogs.com/xinxue/p/7597897.html

计算机视觉中，常用的有三个坐标系：图像坐标系、相机坐标系和世界坐标系。

  它们之间的关系，可以通过三个变换来表示：仿射变换，投影变换，刚体变换。这三个变换是三维重构几何框架的基础。

  如下所示，通过这三个变换，可将三维空间中的点坐标 (Xw, Yw, Zw)，与二维图像中的像素坐标 (u, v) 对应起来。

    

1  图像坐标系

  图像坐标系，是在像平面内，以二维图像为基准所建立的坐标系。根据单位的不同，可分为 像素坐标 (单位 = 像素个数) 和 物理尺寸坐标 (单位 = mm)

1.1  分类

  像素坐标 (u, v) 中，原点 为图像左上角点，坐标轴 为 u 轴 和 v 轴，表示物体所在的行数和列数

  物理尺寸坐标 (x, y) 中，原点 为图像的主点，也即光轴与像平面的交点，坐标轴 为 x 轴 (平行 u 轴) 和 y 轴 (平行 v 轴)，表示物体的尺寸大小

     

1.2  仿射变换

　当相机调整好焦距后，相机透镜中心点到像平面的距离是固定的，此时，像平面内每个像素的尺寸大小也变成了固定值。

    假设每个像素在 x 轴和 y 轴 方向上的物理尺寸分别为 dx 和 dy，则在忽略相机成像畸变的情况下，像素坐标和物理尺寸坐标的转换关系如下：

　

　两者的齐次坐标转换关系为：

  

   这样，就建立了图像中，像素坐标和物理尺寸坐标之间的对应关系。

 

2  相机坐标系

  相机坐标系 (Xc,Yc,Zc)(Xc,Yc,Zc)中，原点 为相机透镜的中心，坐标轴 Xc 轴与 x 轴平行，Yc 轴与 y 轴平行，Zc 轴与相机光轴重合

2.1  小孔成像　

  相机是三维物体和所成二维图像之间的一种映射，常用的小孔成像模型，如下图所示：

     

2.2  投影变换

    设相机的焦距为 f，则根据小孔成像模型，可知相机坐标系下空间点 (Xc,Yc,Zc)(Xc,Yc,Zc)，与物理尺寸坐标 (x,y)(x,y) 的关系如下：

    

   像素坐标 (u,v)(u,v) 与相机坐标点 (Xc,Yc,Zc)(Xc,Yc,Zc) 的关系为：

   

 

3  世界坐标系

  世界坐标系，是实际物体位置的参考系，它和 相机坐标系 的转换关系，就是一个刚体变换，具体见 立体视觉 之 刚体变换

 

  这样，就建立了图像中的 像素点 (u, v) 和 世界坐标中的 空间点 (Xw, Yw, Zw) 之间的对应关系。

  世界坐标系，可根据运算的方便，来自由放置。若世界坐标系和相机坐标系重合，则 RR 为单位矩阵，TT 为零矩阵，即：

  

 

小结

  这样，像素点 (u, v)， 通过相机内参 A，转换为相机坐标下的 (Xc, Yc, Zc)，再经过 RTRT 变换，便可得到世界坐标下的 (Xw, Yw, Zw)

   

后记

  实际上，这有两个问题：第一，上式中的 ZcZc 未知；第二，一个像素坐标点 (u,v)，虽能转化为空间点坐标 (Xw, Yw, Zw)，但并没有 成像物体的特征点 与其对应

  这里有两种解决思路：一种是 双目视觉，另一种是 结构光

 

 参考资料

     <视觉测量> 张广军，第2章，第 7章

转自 https://www.cnblogs.com/xinxue/p/7597897.html