随机森林算法（Random Forest）的二分类问题

1. 数据导入

library(dplyr) #数据处理使用
library(data.table) #数据读取使用
library(randomForest) #RF模型使用
library(caret) # 调参和计算模型评价参数使用
library(pROC) #绘图使用
library(ggplot2) #绘图使用
library(ggpubr) #绘图使用
library(ggprism) #绘图使用
library(skimr) #查看数据分布
library(caTools) #训练集和测试集划分
setwd("D:/BaiduNetdiskDownload")
# 读取数据
data <- fread("data.txt",data.table = F)  # 替换为你的数据文件名或路径
as.data.frame(data)
skim(data)#数据鸟瞰
colnames(data)
hist(data$feature7, breaks = 50) # 查看数据分布

data <- data[1:1000, ] # 选择前1000个样本进行计算

  数据一共包含了35723个样本，214个特征，选择其中前1000个样本进行模型构建（数据太大，这样更快一些）。

  查看一下数据分布情况，是不是符合一定的规律，如正态性之类的。

2. RF模型构建

  数据集分割为训练集和测试集

# 分割数据为训练集和测试集
set.seed(123)  # 设置随机种子，保证结果可复现
split <- sample.split(data$type, SplitRatio = 0.8)  # 将数据按照指定比例分割
train_data <- subset(data, split == TRUE)  # 训练集
test_data <- subset(data, split == FALSE)  # 测试集

# 定义训练集特征和目标变量
X_train <- train_data[, -1]
y_train <- as.factor(train_data[, 1]) #将第一列的标签转换为因子变量

2.1 调参：mtry和ntree

  mtry：随机选择特征数目

# 2.1 mtry的取值是平方根（对于分类问题）或总特征数的三分之一（对于回归问题）
# mtry: 表示每棵决策树在进行节点分裂时考虑的特征数量
# 创建训练控制对象
ctrl <- trainControl(method = "cv", number = 10) # 选择10折交叉验证。
# 定义参数网格
grid <- expand.grid(mtry = c(2: 6))  # 每棵树中用于分裂的特征数量，这里只是随便给的测试，主要为了介绍如何调参，并非最优选择。

# 使用caret包进行调参
rf_model <- train(x = X_train, y = y_train,
                  method = "rf",
                  trControl = ctrl,
                  tuneGrid = grid)

# 输出最佳模型和参数
print(rf_model)

结果：

Random Forest 

800 samples
213 predictors
  2 classes: 'malignant', 'normal' 

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 720, 720, 720, 721, 720, 719, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa    
  2     0.9650768  0.9060232
  3     0.9663268  0.9098219
  4     0.9650768  0.9065433
  5     0.9675768  0.9138408
  6     0.9675768  0.9141520

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 5.

选择mtry=5即可

  ntree：

# 调整Caret没有提供的参数
# 如果我们想调整的参数Caret没有提供，可以用下面的方式自己手动调参。
# 用刚刚调参的最佳mtry值固定mtry
grid <- expand.grid(mtry = c(5))  # 每棵树中用于分裂的特征数量

# 定义模型列表，存储每一个模型评估结果
modellist <- list()

# 调整的参数是决策树的数量
for (ntree in c(50, 70, 90)) {
  set.seed(123)
  fit <- train(x = X_train, y = y_train, method="rf", 
               metric="Accuracy", tuneGrid=grid, 
               trControl=ctrl, ntree=ntree)
  key <- toString(ntree)
  modellist[[key]] <- fit
  print(ntree)
}

# compare results
results <- resamples(modellist)
# 输出最佳模型和参数
summary(results)

结果：

Call:
summary.resamples(object = results)

Models: 50, 70, 90 
Number of resamples: 10 

Accuracy 
     Min.  1st Qu.    Median      Mean 3rd Qu.      Max. NA's
50 0.9500 0.962500 0.9748418 0.9687492   0.975 0.9875000    0
70 0.9375 0.953125 0.9688233 0.9637647   0.975 0.9750000    0
90 0.9375 0.962500 0.9748418 0.9674838   0.975 0.9876543    0

Kappa 
        Min.   1st Qu.    Median      Mean   3rd Qu.      Max. NA's
50 0.8624248 0.9016393 0.9330971 0.9177543 0.9354318 0.9682035    0
70 0.8360656 0.8754931 0.9164091 0.9043374 0.9354318 0.9373532    0
90 0.8360656 0.8992677 0.9330971 0.9144723 0.9354318 0.9673519    0

选择ntree为90即可

2.2 运行模型

# 使用最佳参数训练最终模型
final_model <- randomForest(x = X_train, y = y_train,mtry = 5,ntree = 90)
# 输出最终模型
print(final_model)

结果：

Call:
 randomForest(x = X_train, y = y_train, ntree = 90, mtry = 5) 
               Type of random forest: classification
                     Number of trees: 90
No. of variables tried at each split: 5

        OOB estimate of  error rate: 2.38%
Confusion matrix:
          malignant normal class.error
malignant       586      5 0.008460237
normal           14    195 0.066985646

3. 模型测试

# 在测试集上进行预测
X_test <- test_data[, -1]
y_test <- as.factor(test_data[, 1])
test_predictions <- predict(final_model, newdata = test_data)

# 计算模型指标
confusion_matrix <- confusionMatrix(test_predictions, y_test)
accuracy <- confusion_matrix$overall["Accuracy"]
precision <- confusion_matrix$byClass["Pos Pred Value"]
recall <- confusion_matrix$byClass["Sensitivity"]
f1_score <- confusion_matrix$byClass["F1"]

# 输出模型指标
print(confusion_matrix)
print(paste("Accuracy:", accuracy))
print(paste("Precision:", precision))
print(paste("Recall:", recall)) # sensitivity
print(paste("F1 Score:", f1_score))

结果：

> print(confusion_matrix)
Confusion Matrix and Statistics

           Reference
Prediction  malignant normal
  malignant       146      3
  normal            2     49
                                          
               Accuracy : 0.975           
                 95% CI : (0.9426, 0.9918)
    No Information Rate : 0.74            
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.9346          
                                          
 Mcnemar's Test P-Value : 1               
                                          
            Sensitivity : 0.9865          
            Specificity : 0.9423          
         Pos Pred Value : 0.9799          
         Neg Pred Value : 0.9608          
             Prevalence : 0.7400          
         Detection Rate : 0.7300          
   Detection Prevalence : 0.7450          
      Balanced Accuracy : 0.9644          
                                          
       'Positive' Class : malignant       
                                          
> print(paste("Accuracy:", accuracy))
[1] "Accuracy: 0.975"
> print(paste("Precision:", precision))
[1] "Precision: 0.979865771812081"
> print(paste("Recall:", recall)) # sensitivity
[1] "Recall: 0.986486486486487"
> print(paste("F1 Score:", f1_score))
[1] "F1 Score: 0.983164983164983"

4.绘制混淆矩阵

# 绘制混淆矩阵热图
# 将混淆矩阵转换为数据框
confusion_matrix_df <- as.data.frame.matrix(confusion_matrix$table)
colnames(confusion_matrix_df) <- c("cluster1","cluster2")
rownames(confusion_matrix_df) <- c("cluster1","cluster2")
draw_data <- round(confusion_matrix_df / rowSums(confusion_matrix_df),2)
draw_data$real <- rownames(draw_data)
draw_data <- melt(draw_data)

ggplot(draw_data, aes(real,variable, fill = value)) +
  geom_tile() +
  geom_text(aes(label = scales::percent(value))) +
  scale_fill_gradient(low = "#F0F0F0", high = "#3575b5") +
  labs(x = "True", y = "Guess", title = "Confusion matrix") +
  theme_prism(border = T)+
  theme(panel.border = element_blank(),
        axis.ticks.y = element_blank(),
        axis.ticks.x = element_blank(),
        legend.position="none")

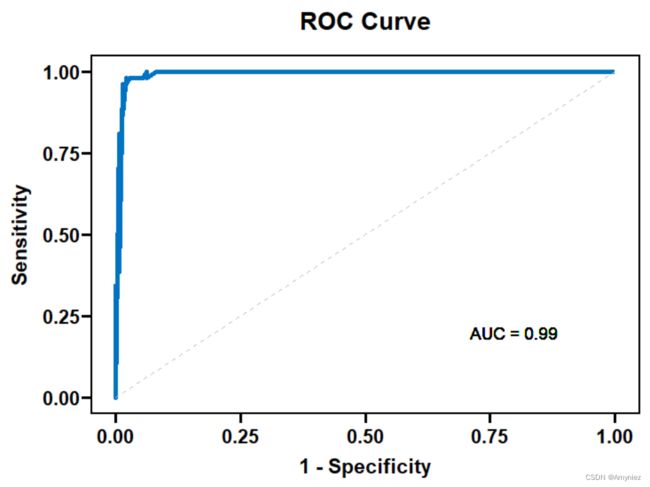
5.绘制ROC曲线

# 绘制ROC曲线需要将预测结果以概率的形式输出
test_predictions <- predict(final_model, newdata = test_data,type = "prob")

# 计算ROC曲线的参数
roc_obj <- roc(response = y_test, predictor = test_predictions[, 2])
roc_auc <- auc(roc_obj)

# 将ROC对象转换为数据框
roc_data <- data.frame(1 - roc_obj$specificities, roc_obj$sensitivities)

# 绘制ROC曲线
ggplot(roc_data, aes(x = 1 - roc_obj$specificities, y = roc_obj$sensitivities)) +
  geom_line(color = "#0073C2FF", size = 1.5) +
  geom_segment(aes(x = 0, y = 0, xend = 1, yend = 1), linetype = "dashed", color = "gray") +
  geom_text(aes(x = 0.8, y = 0.2, label = paste("AUC =", round(roc_auc, 2))), size = 4, color = "black") +
  coord_cartesian(xlim = c(0, 1), ylim = c(0, 1)) +
  theme_pubr() +
  labs(x = "1 - Specificity", y = "Sensitivity") +
  ggtitle("ROC Curve") +
  theme(plot.title = element_text(size = 14, face = "bold"))+
  theme_prism(border = T)

6. 参考

• 机器学习之分类器性能指标之ROC曲线、AUC值