【Matlab】数据插值

数据插值

插值与拟合的区别：

1. 实现方法：插值要求曲线穿过样本点，而拟合不需要穿过样本点，只要求总体误差最小。
2. 结果形式：插值是分段逼近样本点，没有同一的逼近函数；函数拟合则用一个函数去逼近，有完整的表达式。
3. 侧重点：插值可以用于估计区间内某些点对应的函数值；拟合不仅可以估计区间内的点，也可以预测区间外的点。
4. 应用场合：插值多用于精确数据集；拟合多用于统计数据集。

数据插值的作用：在给定的若干数据中，模拟出一条曲线贯穿这些已知数据，我们便可以根据曲线得到未知点的数据信息。

interp1函数

Y1=interp1(X,Y,X1,method)：一维插值函数。根据X、Y的值，计算函数在X1处的值。其中，X、Y是两个等长的已知向量，分别表示采样点和采样值。X1是一个向量或标量，表示要插值的点。

method为字符串，可选值有：

1. linear，默认，线性插值，折线状。
2. nearest，最近插值，阶梯状。
3. pchip，分段三次多项式插值，满足在若干节点处相邻段插值函数的一阶导数相等，比较光滑。
4. spline，三次样条插值，分段构造三次多项式，满足在各个节点处具有连续的一阶和二阶导数，非常光滑。

为什么’pchip’和’spline’这两种插值方法都用3次多项式而不用更高次的？

多项式次数并非越高越好。次数越高，越容易产生震荡而偏离原函数，这种现象称为龙格（Runge ）现象。

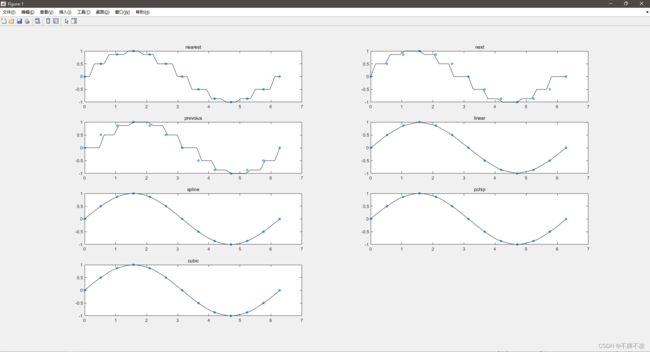
%% 全部的插值方式
xdata=0:pi/6:2*pi;
ydata=sin(xdata);
x=0:pi/20:2*pi;
subplot(4,2,1)
y=interp1(xdata,ydata,x,'nearest');
plot(xdata,ydata,'p',x,y,'k-')
title('nearest')
subplot(4,2,2)
y=interp1(xdata,ydata,x,'next');
plot(xdata,ydata,'p',x,y,'k-')
title('next')
subplot(4,2,3)
y=interp1(xdata,ydata,x,'prevoius');
plot(xdata,ydata,'p',x,y,'k-')
title('prevoius')
subplot(4,2,4)
y=interp1(xdata,ydata,x,'linear');
plot(xdata,ydata,'p',x,y,'k-')
title('linear')
subplot(4,2,5)
y=interp1(xdata,ydata,x,'spline');
plot(xdata,ydata,'p',x,y,'k-')
title('spline')
subplot(4,2,6)
y=interp1(xdata,ydata,x,'pchip');
plot(xdata,ydata,'p',x,y,'k-')
title('pchip')
subplot(4,2,7)
y=interp1(xdata,ydata,x,'cubic');
plot(xdata,ydata,'p',x,y,'k-')
title('cubic')

补充：牛顿插值代码：（不知道应用场景）

function s=newtoninterp(xdata,ydata,x) % xdata和ydata为已知点数据，x为要求点数据
%Newton interpolation at notes (xdata,ydata)
n=length(xdata);
s=ydata(1);xx=1;
for k=2:n
    xx=xx.*(x-xdata(k-1));
    for l=k:n
        ydata(l)=(ydata(l)-ydata(k-1))/(xdata(l)-xdata(k-1));
    end
    s=s+xx*ydata(k);
end
end

其他用法以及类似其他函数参考

interp2函数

interp2(x, y, z, x1, y1, method)：二维插值。x、y可为网格数据也可为向量，z为网格数据对应的z坐标，x1、y1为要求数据点信息。

应用

机动车刹车距离问题

在车辆行驶中，从驾驶员看到障碍物开始，到作出判断而采取制动措施停车所需的最短距离叫停车视距。停车视距由三部分组成：一是驾驶员反应时间内行驶的距离（即反应距离)；二是开始制动到车辆完全停止所行驶的距离（即制动距离）;三是车辆停止时与障碍物应该保持的安全距离。其中，制动距离主要与行驶速度和路面类型有关。根据测试，某型车辆在潮湿天气于沥青路面行驶时，其行车速度（单位: km/h）与制动距离（单位：m）的关系如下表所示。

速度	20	30	40	50	60	70	80	90	100	110	120	130	140	150
制动距离	3.15	7.08	12.59	19.68	28.34	38.57	50.4	63.75	78.71	95.22	113.29	132.93	154.12	176.87

假设驾驶员的反应时间为10s，安全距离为10m。请问：

①根据某驾驶员的实际视力和视觉习惯，其驾驶时的有效视距为120m,则其在该路面行车时，时速最高不能超过多少（结果取整）?

②若以表中数据为参考，设计一条最高时速为125km/h的高速公路，则设计人员应该保证驾驶者在公路上任一点的可视距离为多少米？

---

设速度为$v$，停车视距为$d$，反应距离为$d_1$，制动距离为$d_2$，安全距离为$d_3$，反应时间为$a_s$，则
$$d=d_1+d_2+d_3$$
其中，$d_1=a_{s}v$，$d_2$为$v$的函数，$d_3$已知。

第一问：根据某驾驶员的实际视力和视觉习惯，其驾驶时的有效视距（即最大距离）120m，则其在该路面行车时，时速最高不能超过多少（结果取整）?

已知反应时间为10s，安全距离为10m，可采用解方程方法:
$$10v+d_2+10=120$$
存在的问题是，$d_2$是$v$的函数，但是函数关系未知，方程不可解。

下面考虑数据插值方法，以表格中的数据为样本，进行数据插值，计算出120m的停车视距所对应的速度指标。

编程思路：

第一步：建立速度和停车视距向量。

第二步：以1为单位，对采样区间内所有速度进行插值，计算出相应的停车视距。

第三步：求出停车视距120所对应的速度。

第四步：绘图展示。

如何根据停车视距120找到对应的速度？

第一步：令代表停车视距的向量$d_i$减去120，再取绝对值，得到一个新的向量x。
第二步：将x按升序排列，并记录最小元素的序号，该序号即为停车视距120所对应的速度数据在向量$v_i$中的序号。
第三步：根据序号取得速度数据。

v=20:10:150;
vs=v*(1000/3600); % 单位换算 km/s m/s
d1=10*vs;
d2=[3.15,7.08,12.59,19.68,28.34,38.57,50.4,63.75,78.71,95.22,113.29,132.93,154.12,176.87];
d3=10;
d=d1+d2+d3;
vi=20:150;
di=interp1(v,d,vi,'spline'); % 插值
%% 下面是选出等于120对应的横坐标的方法，方法不唯一！
%% 选出和120差值最小的数对应的横坐标
x=abs(di-120);
[y i]=sort(x);
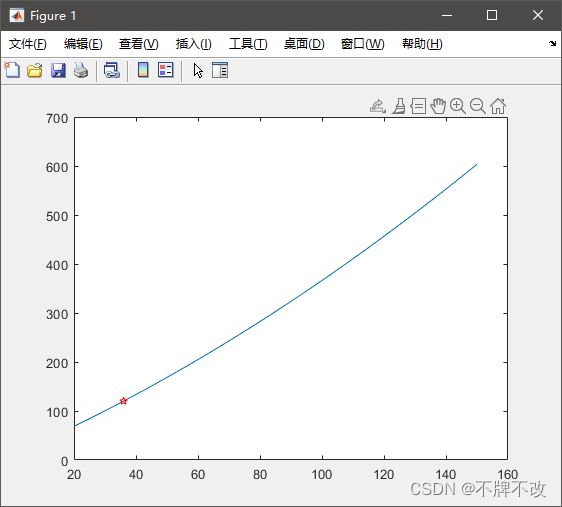
vi(i(1)) % 第一个就是最小的 % 36
plot(vi,di,vi(i(1)),di(i(1)),'rp') % 满足要求的点

第二问：设计一条最高时速为125km/h的高速公路，则设计人员应该保证驾驶者在公路上任一点的可视距离为多少米？

j=find(vi==125); % 找到最高时速为125对应的距离所在索引
di(j)
plot(vi,di,125,di(j),'rp')

沙盘制作问题

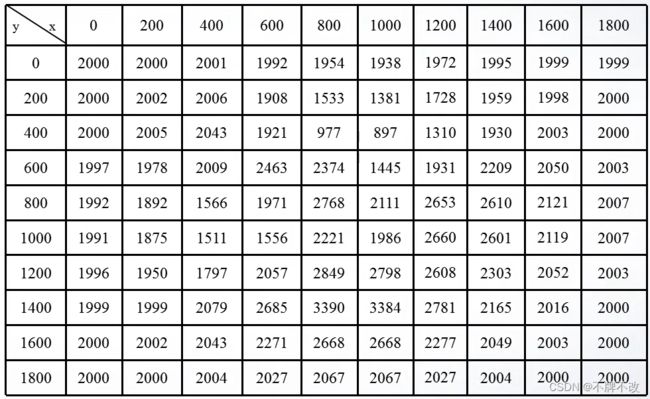
某地面部队分成红蓝两方在指定的陌生区域（平面区域[0，2000]×[0，2000]内，单位：m）进行作战演习。在演习过程中，红方侦查单位已经测得一些地点的高程如下表所示。

①根据表中数据,制作军事沙盘。

②在演习范围内，占领最大高地的一方将获得居高临下的优势。请问红方应第一时间抢占哪块区域。

---

解题思路：

第一问：用二维插值估算数据，以方便制作军事沙盘。

第二问：在插值的基础上，绘制等高线图，找到最大高地。

x=0:200:1800;
y=x;
z = [2000,2000,2001,1992,1954,1938,1972,1995,1999,1999;
     2000,2002,2006,1908,1533,1381,1728,1959,1998,2000;
     2000,2005,2043,1921, 977, 897,1310,1930,2003,2000; 
     1997,1978,2009,2463,2374,1445,1931,2209,2050,2003;
     1992,1892,1566,1971,2768,2111,2653,2610,2121,2007;
     1991,1875,1511,1556,2221,1986,2660,2601,2119,2007;
     1996,1950,1797,2057,2849,2798,2608,2303,2052,2003;
     1999,1999,2079,2685,3390,3384,2781,2165,2016,2000;
     2000,2002,2043,2271,2668,2668,2277,2049,2003,2000;
     2000,2000,2004,2027,2067,2067,2027,2004,2000,2000];
surf(x,y,z);
colormap(mycolor)

%% 插值后
x1=0:100:1800; % 以100为间隔
y1=x1';
z1=interp2(x,y,z,x1,y1,'spline');
figure(2)
surf(x1,y1,z1);
colormap(mycolor)

x1=0:50:1800; % 以50为间隔
y1=x1';
z1=interp2(x,y,z,x1,y1,'spline');
figure(3)
surf(x1,y1,z1);
colormap(mycolor)

%% 绘制等高线
figure(4)
[c h] = contourf(x1, y1, z1, 10)
clabel(c, h) % 显示等高线表示的高度
colorbar % 显示高度配色表
colormap(mycolor)

%% 以下仅为我喜欢的配色图而已
mycolorpoint=[[0 0 16];
    [8 69 99];
    [57 174 156];
    [198 243 99];
    [222 251 123];
    [239 255 190]];
mycolorposition=[1 11 33 50 57 64];
mycolormap_r=interp1(mycolorposition,mycolorpoint(:,1),1:64,'linear','extrap');
mycolormap_g=interp1(mycolorposition,mycolorpoint(:,2),1:64,'linear','extrap');
mycolormap_b=interp1(mycolorposition,mycolorpoint(:,3),1:64,'linear','extrap');
mycolor=[mycolormap_r',mycolormap_g',mycolormap_b']/255;
mycolor=round(mycolor*10^4)/10^4;%保留4位小数

contour函数和contourf函数讲解

这里只讲解基础用法：

[c,h] = contourf(X,Y,Z,t); X、Y为网格数据或向量（与mesh中的参数用法一致），Z是函数值，t为等高线之间的间距和等高线标注的范围（可理解为越大等高线越密集）；返回值不知道含义。

clabel(c, h) ：标注等高线的高度（虽然不知道返回值含义，但可以直接使用）。

colorbar：配色标注。

contour函数与contourf函数用法一致，只是contour显示的是线条，线条间没有颜色填充；而contourf线条间有颜色填充。

figure('NumberTitle', 'off', 'Name', 'contourf'); % 修改图窗名称
contourf(x1, y1, z1, 10)
title('contourf')
colormap(mycolor)
figure('NumberTitle', 'off', 'Name', 'contour');
contour(x1, y1, z1, 10)
title('contour')
colormap(mycolor)